Стационарные решения задач диффузии реакционной смеси
Автор: Русаков Леонид Сергеевич, Русаков Сергей Владимирович, Талибуллин Ринат Русланович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (1), 2010 года.
Бесплатный доступ
Получены аналитические решения для двух одномерных задач, описывающих поведение реакционно-диффузионной смеси на конечном и бесконечном промежутках. Методика получения решения состоит в "обращении" задачи, когда искомые параметры считаются заданными и через них определяются исходные данные.
Короткий адрес: https://sciup.org/14729644
IDR: 14729644 | УДК: 534.983
Текст научной статьи Стационарные решения задач диффузии реакционной смеси
ВЕСТНИК ПЕРМСКОГО УНИВЕРСИТЕТА
Математика. Механика. Информатика
Вып.1(1)
Стационарные решения задач диффузии реакционной смеси
Л. С. Русаков, С. В. Русаков, Р. Р. Талибуллин
Пермский государственный университет, 614990, Пермь, ул. Букирева, 15
Получены аналитические решения для двух одномерных задач, описывающих поведение реакционно-диффузионной смеси на конечном и бесконечном промежутках. Методика получения решения состоит в "обращении" задачи, когда искомые параметры считаются заданными и через них определяются исходные данные.
Во многих природных явлениях наблюдаются распространяющиеся и стационарные фронты, разделяющие различные состояния системы. Такие процессы, как распространение эпидемий, популяций, химических реакций, на первый взгляд непохожие, оказываются схожими по диффузии (позволяющей агенту химической реакции или эпидемии распространяться) и реакции (переход явления в разные состояния или взаимодействие химических компонентов). Подобные явления называются реакционно-диффузионными системами (РДС). В настоящей работе мы рассмотрим некоторые стационарные решения для простейшей модели РДС [1]. Целый ряд таких решений получен ранее в задаче о конвективном течении РДС в вертикальном канале при подогреве его сбоку [2].
1. Постановка задачи
Рассмотрим систему одномерных уравнений в частных производных, описывающих поведение активатора и ингибитора [1] соответственно:
д U ( t , x ) д 2 U ( t , x )
-
= - U ( t , x ) - V ( t , x ) +
д t д x 2 (1Л)
+ H(U ( t , x ) - a ),
-
- 1 д v ( t , x ) _2 д2 v ( t , x )
-
( a ) ^^ = г -^2~ — V ( ' • x > + (1.2)
+ ^U (t, x), где функция
H(f) = J1’ f - 0,(1.3)
[ 0, f < 0
уровень активации a = a0 + a(S - So), 0 < a < 1,(1.4)
S = j(U (t, x) + V (t, x ))dx.(1.5)
Параметры задачи:
г, a, ^, a0 > 0, a, So > 0.(1.6)
2. Стационарное решение
Очевидно из формальных соображений, положив a0 = a 0 - a SQ , можно сократить число параметров, при этом (1.4) примет вид a = a 0 + a S .
В стационарном случае система уравнений (1.1)-(1.2) примет вид
U "( x ) - U ( x ) - V ( x ) + H ( U ( x ) - a ) = 0 , (2.1) г 2 V "( x ) - V ( x ) + ^ U ( x ) = 0. (2.2)
Для системы уравнений (2.1)–(2.2) рассмотрим две краевые задачи.
Задача I. U ( ± да ) = V ( ± да ) .
Задача II. U '( ± 1 ) = V '( ± 1 ) .
Будем искать аналитическое решение исходя из следующих предположений:
-
1) "Финитность носителя"
U ( x ) > a , x e ( - % , % ),
U ( ± % ) = a .
2) "Гладкость"
U ( x ), V ( x ) e C ';
(2.3)
(2.4)
Будем анализировать случай действи тельных и различных корней (D > 0), тогда
возникает естественное ограничение на пара-
искомые функции непрерывно дифференцируемы во всей области определения.
3) "Симметричность" - решение симметрично относительно точки x = 0 .
Качественный вид такого решения представлен на рис. 1.
метры задачи
U< 4s!
Очевидно, в этом случае
A < A < 0 < A < A . (2.8)
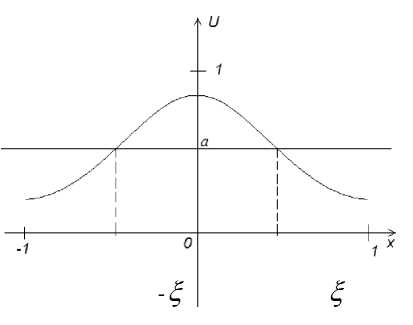
Рис. 1. Качественный вид стационарного решения
Будем рассматривать решение в трех областях аргумента и соответственно их индексировать: 1 - x < - % ; 2 - | x | < % ; 3 - x > % .
В этом случае общее решение для функции V ( x ) можно записать в виде
V ( x ) = Е c , - e " + c k 4 , k = 1 ’ 2,3 , (2.9) i = 0
где очевидно ci4 = c3 4 = 0 , а из уравнения
(2.6) нетрудно получить, что с2 4 =-----.
’ 1 + и
Подставив решение (2.9) в равенство (2.5),
получаем
( 3
U(x)=и-1 Е dick, ie у i=0
Ax । „
+ c k ,4 ’ У
k = 1,2,3 ,
Из (2.2) выразим
U ( x ) = u 1 ( V ( x ) - s 2 V "( x ) ) .
Подставив (2.5) в (2.1), получим
Viv ( x ) - ( 1 + s2 ) V\x ) + s 2 ( 1 + u ) V ( x ) —
где d = 1 -
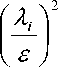
- us 2 H ( x ) = 0,
(2.5)
(2.6)
где
H ( x ) =
1, l o,
x e [ - ^ , % ]
x £ [ - % , % ].
Характеристическое уравнение для ли-
нейного ОДУ с постоянными коэффициента-
ми (2.6) имеет вид
A4 - ( 1 + s 2 ) a 2 + s 2 ( 1 + u ) = 0 .
Из соображений симметрии решения следует V ( - % + 0) = V ( % - 0) . Откуда, с учетом свойств корней характеристического уравнения, получаем
-a% -A% A% A% c2 oe 0 + c2 e 1 % + c2 2e 1 % + c2 3e 0 =
A% A% - A% - A%
= c2,0 e 0 + c2,1e + c 2,2 e + c 2,3 e 0
и
( c 2,0 - c 2,3 ) sh ( A 0 % ) + ( c 2,1 - c 2,2 ) sh ( A 1 % ) = 0.
Его корни:
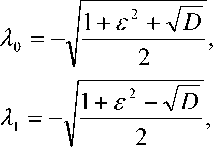
Следовательно,
c 2,3 = c 2,0 ’
c 2,1 = c 2,2 .
(2.7)
Тогда, не нарушая общности, можно записать
V ( x ) = C2>0 ch ( A x ) + C2>1 ch ( A x ) + C 2 4, (2.10)
A = -A, a =-a , где
D = ( 1 + s 2 ) 2 - 4 s 2 ( 1 + u ) •
U ( x ) = uA d 0 C 2 , 0 ch ( A 0 x ) + d 1 C 2 , 1 ch (A x ) + C 2 , 4 ) .(2.11)
3. Решение задачи I
Получим решение при x > % (область 3), которое удобнее записать в виде 3
V (x) = £ C e(x- %), i=0 (3.1)
U ( x ) = f d t C 3е » x - % > .
i = 0
Из краевого условия и свойств собственных значений (2.8) следует, что C 3,2 = C 3,3 = 0 .
Таким образом, для построения решения необходимо определить коэффициенты C , C , C , C и значение величины % = % (a ) . Для этого имеем набор условий, вытекающих из "гладкости" искомых функций (2.4.), и определяющего условия (2.3), которые мы сформулируем в следующем виде:
V (% - 0) = V (% + 0),(3.2)
U (% - 0) = U (% + 0),(3.3)
V'(% - 0) = V'(% + 0),(3.4)
U'(% - 0) = U'(% + 0),(3.5)
U(% + 0) = a.(3.6)
Подставив решения (3.1) в соотношения (3.2)–(3.6), получим систему уравнений:
C 2,0 ch ( ^ 0 % ) + C 2,1 ch2 % ) + C 2,4 = C 3,0 + C 3,1 , (3.7)
. ___________ d 0 -1 ___________r
2,1 = ( d 0 - d 1 )( sh ( 2 1 % ) - ch ( 2 1 % )) C 2,4
Используя свойства гиперболических
синусов-косинусов и определение величин d , окончательно имеем
C = 2,0
2 2 e
2 2 - 2 0
C 2,4 , C 2,1
2 0 e 2 %
2 2 - 2 0
r .
2,4 ,
(3.12)
= 2 ( e 2 2% - 1 ) C , C 2 ( e 2 % -1 • .
2( 2 - 2 2 ) 24 34 2( 2 2 - 2 0 ) 2 ’ 4
(3.13)
Тогда из условия (3.6) находим a = ^ (d 0 C 3,0 + d 1 C 3,1 ) =
_1 11 _ Ade^- 2 ^1
2 ( 1 + ^ 2 2 - 2 2 J
Вид функции a = a ( % ) представлен на рис. 2.
d 0 C 2,0 ch ( 2 0 % ) + d 1 C 2,1 ch ( 2 1 % ) + C 2,4 =
d 0 C 3,0
+ d 1 C 3,1 ,
(3.8)
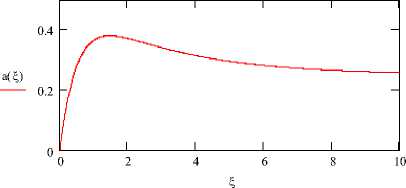
Рис. 2. Функция a = a ( % ) при £ = 0.125, ^ = 1
2 0 C 2,0 sh ( 2 0 % ) + 2 1 C 2,1 sh ( 2 1 % ) =
= 2 0 C 3,0 + 2 1 C 3,1 ,
(3.9)
Видно, что функция a = a ( % ) имеет
один экстремум и асимптоту при % 2 да .
20 d0C20sh ( 2% ) + ^ dC^sh ( 2% ) =
Определим их значения. При % 2 да из соот-
= 2 0 d 0
C
3,0
+ 2 1 d 1 C 3,1
(3.10)
Будем решать задачу в следующей последовательности: из уравнений (3.9)–(3.10) нетрудно выразить
C ... = C 2,0 sh ( 2 0 % ) , C 3., = C 2., sh ( 2 , % ) . (3.11)
ношений (3.13) получаем
С =---- 1---С С =
C 3,0 о/„2 л2Л C 2,4 ’ C 3,1
2( 2 1 2 0 )
Отсюда a
- 2 0 2( 2 2 - 2 0 )
2 ( 1 + ^ ) .
Из соотношения a ' ( % ) = 0 имеем
С
2,4
.
Подставив соотношения (3.11) в уравнения (3.7)–(3.8), получаем
C2,0 (sh(20%) - ch(20%)) + C2,1 (sh(2%) - ch(2%) = C2,4, d0C2,0 (sh2) - ch(20%)) + d 1C2,1 (sh(2%) - ch(21%)) = C2,4 •
Откуда
% * =
2 ( 2 0 - 2 1 )
( 2 0 d 1 ^
1 2 1 d 0 J
C 2,0
__________ d 1 -1 __________c
( d 1 - d 0 )( sh ( 2 0 % ) - ch ( 2 0 % )) 2,4
Таким образом, при ax < a < a ( % ) каждому значению a соответствует два значения % . Например, для £ = 0.125, ^ = 1 при
a = 0.3 получаем £ (0.3) = 0.5664 и £ (0.3) = 4.695 . Для сравнения на рис. 3 и 4 приведены распределения искомых функций при этих значениях параметров.
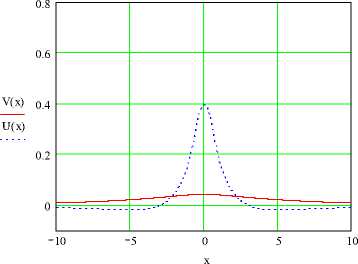
Рис. 3. Функции V ( x ), U ( x ) при
£ = 0.125, a = 1, £ = 0.5664
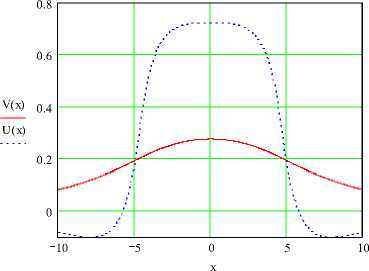
Рис. 4. Функции V ( x ), и ( x ) при £ = 0.125, A = 1, £ = 4.695
Для определения параметров соотношения (1.4) необходимо найти значение величины S . Решим эту задачу в общем случае.
S = J ( u ( x ) + V ( x ) ) dx = -да
= (1 + a 4 J V ( x ) dx - A 4 £ - 2 J V "( x ) dx . -да -да
В силу непрерывности функции V '( x ) второе слагаемое в этом выражении обращается в 0. Тогда, из соображений симметрии, можно ограничиться вычислением интеграла да £ да
J V ( x ) dx = J V ( x ) dx + J V ( x ) dx = C2 £
0 0 £
Откуда
S = 2 ( 1 + A - 1 ) c 24 £ = 2 £ . (3.14)
Таким образом, a = a0 + 2a£(a); (3.15)
и из данного выражения, задав a 0< a , можно определить соответствующую величину a . С другой стороны, при заданных значениях паров a 0, a значение величины a определяется как решение трансцендентного уравнения (3.15), которое может не иметь решения или имеет одно или два решения.
4. Решение задачи II
Нетрудно показать, что учет краевых условий в этом случае позволяет, не нарушая общности, записать решение при x е [ £ ,1] (область 3) в виде
V ( x ) = C30ch ( Л ( 1 - x )) + C31ch ( ^ ( 1 - x )) ,(4.1)
U ( x ) = a - 1 ( doC3;Och ( ^ 0 ( 1 — x )) + + d.C^ch ( ^ ( 1 - x )) )
(4.2)
Подстановка решений (2.10)–(2.11), (4.1), (4.2) в условия (3.2)–(3.5) дает уравнения вида
C 2,0 ch ( Л£ ) + C 21 ch Л ) + C 2,4 =
= C3,0 ch (Л0 (1 - £))+ C3,1 ch (Л, (1 - £)),()
d0C2fich ( ^£ ) + dC^ch ( ^£ ) + C2 4 =
= d 0 C 3,0 ch ( Л 0 ( 1 - £ )) + d 1 C 3,1 ch ( Л 1 ( 1 - £ )), (4.4)
Я 0 C 2,0 sh ( Л 0 £ ) + Л 1 C 2,1 sh ( Л 1 £ ) =
= Л0 C 3,0 ch (Л0 (1 - £))+Л1C 3,1 ch (Л1 (1 - £)),
Л d0 C2,0 sh Л) + Л1 d1C2,1 sh (Л£) =
= Л 0 d 0 C 3,0 ch ( A, ( 1 - £ )) + Л 1 d^ch ( Л 1 ( 1 - £ )).
Из уравнений (4.3)–(4.4) нетрудно выразить sh(Л0£) , c sh(Л£) . (4.7)
-
C 3,0 = - C 2,0 sh Л ( 1 - £ )) 31 = 21 sh ( Л 1 ( 1 - £ ))
Подставив соотношения (4.7) в уравнения (4.5)–(4.6), получаем
C 2.1 = - T - d T ( ch ( Л 1 £ ) + sh ( Л 1 £ ) cth ( Л 1 ( 1 - £ )))- 1 C 2,4 .
d j d
Используя свойства гиперболических сину- сов-косинусов и определение величин d , окончательно имеем
Откуда получаем свойство (3.14) S = 2 A .
Типичный вид решения задачи II представлен на рис. 6.
= _ a 2 sh ( Л о ( 1 - ^ ))
A2 - Л2 sh (Л0)
Л о sh ( Л 1 ( 1 - A ))
A2 - Л2 sh (A)
A2 sh ( Л о A )
A2 - Л2 sh (Ло)
= _ Л 0 sh ( Л 1 А )
A -Л2 sh(A)
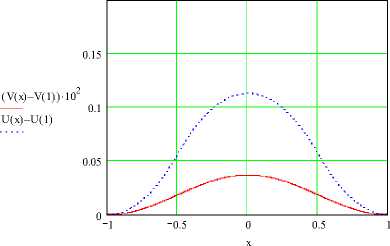
Рис. 6. Решение задачи II при s = о.125, ^ = 2 , A = о.5, a (Q.5) = Q.1667
Тогда из соотношения (3.6) находим a = ц 1 ( d о C 3,0 ch ( Л о ( 1 - A )) + d i C 3,1 ch ( A ( 1 - A>
Вид функции a = a ( A ) представлен на рис. 5. В данном случае, в отличие от функции в задаче I, она имеет монотонный характер.
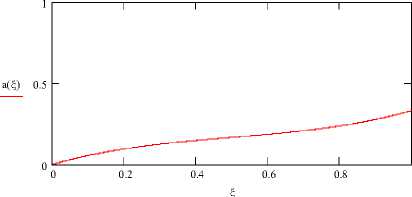
Рис. 5. Вид функции a ( A ) при s = 0.125, ^ = 2
Определим величину S . Для этого вычислим интеграл
1 A 1
J V ( x ) dx = j V ( x ) dx + J V ( x ) dx = C A .
оо a
Таким образом, сформулировав "обратную задачу" относительно исходных данных, удалось получить два нетривиальных стационарных решения РДС.
Список литературы Стационарные решения задач диффузии реакционной смеси
- Krischer K., Mikhailov A. Bifurcation to Travellin Spots in Reaction-Diffusion Systems//Physical Review Letters. 1994. V.73, №23. P.3165-3168.
- Русаков Л.С. Аналитическое решение задачи о течении реакционно-диффузионной бинарной смеси в вертикальном слое//III конференция-конкурс грантов аспирантов и молодых ученых механико-математичес-кого факультета Пермского государственного университета: сб. тез. науч. докладов конф. Пермь, 2008. С.60-63.


