Stationary solutions for the Cahn - Hilliard equation coupled with Neumann boundary conditions
Автор: Krasnyuk I.B., Taranets R.M., Chugunova M.
Рубрика: Математическое моделирование
Статья в выпуске: 2 т.9, 2016 года.
Бесплатный доступ
The structure of stationary states of the one-dimensional Cahn - Hilliard equation coupled with the Neumann boundary conditions has been studied. Here the free energy is given by a fourth order polynomial. The bifurcation diagram for existence and uniqueness of monotone solutions for this problem has been constructed. Namely, we find the length of the interval on which the solution monotonically increases or decreases and has one zero for some fixed values of physical parameters. Under the non-uniqueness we understand a possibility of existence of more than one monotone solutions for the same values of physical parameters.
The cahn - hilliard equation, neumann boundary conditions, steady states
Короткий адрес: https://sciup.org/147159372
IDR: 147159372 | УДК: 517.912 | DOI: 10.14529/mmp160206
Текст научной статьи Stationary solutions for the Cahn - Hilliard equation coupled with Neumann boundary conditions
We study the steady state solutions for the Cahn - Hilliard equation (see e.g. [2,4,7,8])
u t = ( —au + yu 3 — U xx ) xx , 0 < x < l, t > 0 ,
coupled with the Neumann boundary conditions ux
= u xxx
= 0 ,
x = 0 , l,
where a and y are some physical parameters. The authors of [2] have considered a structure of stationary solutions of problem (1) - (2) as a function of length l and mass m = f l u ( s ) ds. They have counted the total number of monotone solutions, depending on the parameter values of the problem. In [2] phase portraits of the problem have been constructed which describe the monotone solutions for a special stored-energy function f ( u ) + у( u‘ )2. wlrere e is a, small parameter. In this case, the function f‘ ( u ) has one negative minimum, one positive maximum, and f ( ±ro ) = ±ro.
In this paper, we study the following problem u" = -au + yu 3 — a, u‘ (0) = u‘ (l) = 0,
where a reflects influence of the average mass on qualitative behaviour of solutions: a is the main parameter of the problem because it is related to an interaction energy of the phase decomposition in a binary alloy; 7 is a parameter corresponding to thermodynamically stability of the system. In particular, a = eBT (1 — T), where Tc is the critical temperature of the phase transition for order-disorder in a disordered binary alloy, which can be measured during the cooling process of the alloy; Eint is the interaction energy between atoms of sorts A and B in the binary alloy. The energy functional corresponding to problem (3) can be written in the form
l
E ( u ( t )) = I Q( u ) 2 + f ( u )^ dx,
E (u (t )) = E (u (0)) ,
where the free energy f (u) is f (u) = 7 u4 - °u2 - au + C.
Note that, in the case a > 0 , be reduced to
7> 0.by the re-scaling u = - u(^Ox), problem (3) can u ‘‘ = —u + u3 — a, u ‘ (0) = u ‘(L) = 0,
where L = y OZ and a = a V Y 1 This case was studied in [2,7]. To the best of authors’ knowledge all other cases were not considered in a literature. Therefore, in this article we investigate the existence of nontrivial solutions of problem (3) for all possible values of these parameters. In particular, we study an interesting case when 7 < 0. It should be mentioned that the case 7 < 0 , a < 0 and |a| < a 0 := 4 JY^ leads to a non-uniqueness result (i.e. there exist two solutions with the same initial energy), depending on initial energy, but the solution of the problem is unique when |a| ^ a 0. Also we describe all possible dynamical scenarios for the parameter values.
Moreover, our results can be applied to the Izing model. For example, the Izing model free energy in the vicinity of the phase transition may be written as the following (see, e.g. [6])
f ( u ) = a + ru 2 + su 4 + O ( u 6) .
In order for the system to be thermodynamically stable, the parameter on the highest even power of the order parameter must be positive. In this case, we show that s > 0, hence the free energy is bounded. However, for the Neumann boundary value problem we can consider the case when the "open" system is thermodynamically unstable that corresponds to s < 0. For example, in the case s < 0, r > 0 and a G [0 , 2), a solution is not unique. On the phase plane uOu’, this phenomenon is illustrated by two loops with identical lengths of periods which are both symmetric with respect to the axis Ou. Thus, there are two smooth nontrivial solutions.
1. The Steady State Solutions for the Cahn - Hilliard Equation
In this section, we find the existence interval, L for a monotone solution by considering all possible values of the physical parameters. We proceed by examining all qualitatively different nine cases. Note that since all systems at hands are conservative they cannot have any attracting fixed points. Therefore their phase portraits can have only saddles and/or centers.
I.В. Krasnyuk, R.M. Taranets, M. Chugunova
-ЧП.
XXX 2-Ul
11 tt
XXXI
fl
ft tt
Xll^ ttt V tttt
TT ft tt
0- '
-1
2 xxx
4 4 4/
-2
tf T
ttt
I -■
У
/Mt
At
ttt
.ttt
tt tt
o-'
-1
Xittxxxvvxv XXXXXXXXXXX 44444444444
\Wt
XXft '
JMt ■ 44A4
Wit fttt ttt
ttt
ttt ttt
44 44
3 4 44
-2
-1
чг*,«'^«'*~\
tt tt tt tt
и
Fig 1. Phase diagram for the case a > 0 , y > 0 with a = 0 , 1 on the left and a = 1 on the right
-
1.1. Case a > 0 , y > 0
In this case, by the re-scaling u =
au(Vax), problem (3) can be reduced to u ‘‘ = —u + u3 — a, u ‘ (0) = u ‘ (L) = 0,
where L = д/ a/ and d = aVY* Integrating (6), we find that
( u ‘ )2 u 4 u 2 1
-
—---4 + — + au = p -. ( u‘ )2 = ^( u 4 — 2 u 2 — 4 au + 4 p ) .
Note that the equation u 3 — u — a = 0 has
-
• three real roots
2 z,2kn ф = jarcc0^3/^);
uk = —p cos( ф + -—) , k = 0 , 1 , 2 , з 3
provided that a 2 < 27 (two minimums and one maximum). Thus, we have two nontrivial u ˆ 4 u ˆ 2 u ˆ 4 u ˆ 2
solutions if —max + m2 + au max < p < —min + -^ + au min and the lengths of intervals, where the corresponding solution has only one zero, are
L 0 , 1 =
V2
u 2
/
u 1
dt
/t 4 — 2 t 2 — 4 d t + 4 p ’
u 4
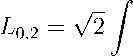
u 3
dt
/t 4 — 2 t 2 — 4 a t + 4 p
where u k are four real roots of the equation t 4 — 2 1 2 — 4 at + 4 p = 0 such that u 1 < u 2 < u ˆ 4 u ˆ 2
u3 < u4. We have only one nontrivial solution if p < —max + -л2ах + arzmax with the length of interval, where the solution has only one zero, given by u2
L 0 , 3 = V 2 j
dt
л/ 1 4 — 2 1 2 — 4 d t + 4 p1
u 1
ttttt
> х х 4 4 4 4
।
ttttt ttttt
u' O-.
ttttt tf ft t ttttt
444 4444 XV 4 4 4 4 4
2 tttt tttt
1 tttt
—
ttttt
-3
-2
t| tl
-1
о
и
V 4
/
4 4444
J 44444 . 44444 ■ 44444 144444
V/44444
«■
0-.
-1
ttt ttt
ttt
tttt tttt tttt
2 tttt
ttttt
-3
-2
-1
О
и
A V VI
/41 V4S /#4 i 4 4444 44444 Fig 2. Phase diagram for the case a > 0, y < 0 with a = 0,1 on the left and a = 1 on the right where uk are taco real roots of the equation t4 — 2t2 — 4dt + 4p = 0 such that u 1 < u2: • one real root a /12 1" \1 /3 a 012 - 1 )1 /3 27/ u min 2' W — 27) + C V T uˆ4 provided that a2> 27 (one minimum). Tims, we 1 iave a nontrivial solution it p < —m + uˆ2 2 + aumin with the length of interval, where the solution has only one zero, given by L 0 = / u2 dt /t4 — 2t2 — 4 a t + 4p, u1 where uk are two real roots of the equation t4— 2t2— 4dt + 4p = 0 such that u 1 < u2: • two real roots a a umin = 2( |)1 /3, ufl = — (|)1 /3 provided that a2= 27 (one minimum). Tims, we 1 iave a nontrivial solution if p < umin + aumin = 2(-2)2/3with the length of interval, where the solution has only one given by 4 umin 4 + zero, u2 L0 = /2 / dt = , J V t4 — 2t2 — 4 at + 4p u1 where uk are the two real roots of the equation t4— 2t2 + 4at — 4p = 0 such that u 1 < u2. Thus, if 0 < L < L0 then the corresponding solution of the problem has no zeros located on the interval (0, L). If kL0< L < (k + 1)L0, where k = 1, 2,..., then the solution lias exactly k zeros located 1.2. Case a > 0, y< 0 In this case, by the re-scaling u = . —au(/ax), problem (3) can be reduced to u ‘‘ = —u — u3 — a, u ‘ (0) = u ‘ (L) = 0, (П) I.В. Krasnyuk, R.M. Taranets, M. Chugunova where L = y^Z and d = aV-a• Integrating (11), we obtain (Ui, ‘ )2 Ut4 u2 „ 1 —--+ — + — + du = p -^ (u‘)2 = ^(—u4 — 2u2- 4du + 4p). Note that the equation u3 + u + d = 0 has only one real root „ ( d П2 Гx1/3 d /d2 1" x1/3 umax = W 2+VZ + 27) + I" 2 -V Т + 27/ for any d G R1 (one maximum). Thus, we have a nontrivial solution if p > umax + umax + dUmax with the length of interval, where the solution has only one zero, given by u2 L0 = V. dt /—t4 — 2t2 — 4 d t + 4 p p u1 where uk are two real roots of the equation t4 + 2t2 + 4dt — 4p = 0 such that u 1 < u2. For example, if d = 0 arid p > 0 then we have (u' )2 + (u2 + 1)2 = 1, where A2 = 4p+l, В4 = 4p + 1, and from (13) it follows that B2-1 1 В2 Г dt _ ~ Г dt A J /в4— (t2 +1)2 = J vci — 12)(i+к2Я’ -√B2-1 -1 where A= B2 A^B2 + 1 ’ k2 B2— 1 B2 + 1 G (0, 1). Let t = sin ф in integral (14). Then L0 = 2A π/2 dφ /1 + k2 sin2ф L0G (2.622A,nA). 1.3. Case a < 0, y > 0 In this case, by the re-scaling u = —au(V—ax), problem (3) can be reduced to u ‘‘ = u + u3 — d, u ‘ (0) = u ‘(L) = 0, (17) where L = V—a Z and d = — a \/—a • Integrating (17), we obtain (u, ‘)2 ? 14 ? 12 1 —2---4 — — + dU = p ^^ (u‘)2 = ^(u4 + 2u2— 4du + 4p). Note that the equation u3 + u — d = 0 has only one real root „ / d /d2 1" x1/3 d d2 Fx1/3 u min =(2 + VZ+27) +G — VT + 27t 444 444 trt 3 1444 4 2 111 I 444 -444 ttt ttt u' 0-' 44 V 144 ft tt trt ttttt ttttt u' -I 44/ 4 4yV ttttt Vt 1111 2 4 4 4 -3 4 4 4# 44 4 / -3 -2 -1 44444V 2-4444 4 V 444444 444444 i t/t t t rr tit 11 i 4444444V 4444444V 44444444 ttt 0-' Ht ttt ttt ttt ttt -I tttttttw^ 4444444/ ttt ttt ttt ttt ttt ttt Fig 3. Phase diagram for the case a < 0, y the right Al t t ; z^-*-*->-<-f->->->s\ 4 4 4 4 1ttt7 >-»->-♦->-►-►-»->'> у V 4 4 4 tttt/ л-*-*-*-*-*-*-*-*ч У V 4 4 4 ttttf i - 0-. tttt tttt tttt] tttt tttt 2 444 44/y ttt 44 4 4 -3 -2 -1 I -1 tttt1» ttttt -3 -2 I и Fig 4. Phase diagram for the case a < 0, y tt tt > 0 with a = 0,1 on the left and CT = 1 on u' ttt Г ttt» 2 tt t i - 0-. -1 ttt ttt ttfl tt tt tt tt tt ttt ttf ttt^a tttt -3 Zy -2 Л4444 > 4444 f 44 t44 4 4 4 4 Z4 Qitttt t/t tttt -1 о и i < 0 with a = 0, 1 on the left and a = 1 on the right for any a E R1 (one minimum). Thus, we 1 nwe a nontrivial solution If p > — umin — umn + aumin with the length of interval, where the solution has only one zero, given by L о = V2 u2 / dt //t4 + 212— 4 a t + 4 p p where uk are two real roots of the equation t4 + 212— 4at + 4p = 0 such that u 1 < u2. 1.4. Case a < 0, y< 0 In this case, by the re-scaling u = . -дu(V—ax), problem (3) can be reduced to u ‘‘ = u — u3 — ст, u ‘ (0) = u ‘ (L) = 0, I.В. Krasnyuk, R.M. Taranets, M. Chugunova where L = V-a l and d = — ^VY' Integrating (19), we find that (Ui ‘ )2 u4 u2 „ 1 —--+ —---^ + du = p ^, (u‘)2= ^(—u4+ 2u2— 4du + 4p). Note that the equation —u3+ u — d = 0 has • three real roots uk = —cos(ф + 2кп), k = 0,1, 2, ф = 1 arccos(3^d); V 3 3 32 provided that d2< 27 (two maximums and one minimum). Thus, we have two nontrivial solutions if umax — umax + dumax < p < umin — umi1 + dumin with the lengths of intervals, where the corresponding solution has only one zero, given by L 0,1 = u2 / u1 dt У—14+ 212— 4 d 1 + 4 p ’ u4 u3 dt У—14+ 212— 4 d 1 + 4p where uk are four real roots of the equation 14 — 212 + 4d 1 — 4p = 0 such that u 1 < u2 < u3 < u4. uˆ4 uˆ2 We have only one nontrivial solution if p > -^--min + dumin with the length of interval, where the solution has only one zero, given by L0,3 = u2 / u1 dt У—14+ 212— 4 d 1 + 4p ’ where uk are two real roots of the equation 14— 212+ 4d 1 — 4p = 0 such that u 1 < u2: • one real root ( d /d2 Г \1/3d /d2" 1 у /3 27/ umax = Г 2 + VT — 27) + 1— 2 — V "4" provided that d2> 27 (one maximum). Thus, лае have a, nontrivial solution If p > umax — uˆ2 -J2ax + dumax with the length of interval, where the solution has only one zero, given by u2 L0 = v2 / u1 dt У—14 + 212 — 4 d 1 + 4p ’ where uk are two real roots of the equation 14 — 212 + 4d 1 — 4p = 0 such that u 1 < u2: • two real roots umax —2(d)1/3, df. = (ф1/3 provided that d2= 27 (one maximum). Thus, лае have a, nontrivial solution If p > umax — 2 umax 2 + и umax given by —2()2/3with the length of interval, where the solution has only one zero, u2 L0 = V2 у u1 dt У—14+ 212— 4 d 1 + 4p1 14V 2 111 ЦК liny 11141 14444» 444441 44444 V T o-' — ini Ч 2 44 4 tj 444# -3 -3 -2 -1 о и ttt fit tft ttt tttt tifttttt tilt tttt tttt tttt tttt to ttt л ttt и ■' ttttf tttti 1 т T T ttt О Ш -1 ttt ttt tttt tttt .мин к ШЛ QtT nt t It I 4t\ th v >4U ttttt -3 -2 -1 ll /«4 4 4 44 i Fig 5. Phase diagram for the case a = 0, y > 0 with a = 0,1 on the left and for the case a = 0, y < 0 with a = 0, 1 on the right where uk are taco real roots of the equation t4 ^^^^^^^^^r 212 + 4at — 4p = 0 such that u 1 < u2- For example, if a = 0 arid p > 0 then we have where A12 4p+1 2 B4 = 4p + 1. L0 B2 A A2 + and from B2+1 ∫ √B4 √B2+1 dt (u 2 — 1)2= 1 B4 ’ (24) it follows that - 1)2 1f -1 dt V(1 - 12)(1 + k212) ’ where A= B2 aVb2— 1 ’ k2 B2 + 1 B2 - > 1. Let t = sin ф in integral (25). Then π/2 L о = 2 A dφ V1 + k2 sin2ф < π A. 1.5. Case a = 0, y = 0 If a = 0, y > 0, by the re-scaling u = u(/x), then problem (3) can be reduced to the one u ‘‘ = u3 — а, u ‘ (0) = u ‘(L) = 0, (28) where L = /^l and a = — T Integrating (28), we find that (u.‘)2 u* 1 —2---4 + au = p ^^ (u )2 = ^(u4— 4au + 4p). I.В. Krasnyuk, R.M. Taranets, M. Chugunova Thus, problem (28) has a nontrivial solution provided that p > 4d4/3, i. e. p > 4(^)4/3. The length of interval, where the solution has only one zero, is L0 - V2 u2 dt V t4- 4 dt + 4p1 u1 where uk are two real roots of the equation t4— 4dt + 4p — 0. If a — 0, y< 0, by the re-scaling u — d(V—Yx), then problem (3) can be reduced to u ‘‘ — —u3— d, u ‘ (0) — u ‘ (L) — 0, where L — V—Y land d — T Integrating (30), we find that (u ‘ )2 u4 1 —--+ — + du — p < > (u )2 — ^(—u4— 4du + 4p). Thus, problem (30) has a nontrivial solution provided that p > — 4d4/3, i. e. p > — 4(^)4/3. The length of interval, where the solution has only one zero, is L 0—V2 u2 dt V—t4— 4 dt + 4 p ’ u1 where uk are two real roots of the equation t4 + 4dt — 4p — 0. For example. if d — 0 and p > 0 then we have the сште (u' )2 u4 A2 +B4 ’ where A2 — 2p, B4 — 4p. Obviously, the length of interval, where the solution has only one zero, is B1 B2dt 2B dt B _ Д L B 2,622 L 0 —A J VBA—T4—A J VT—T* " 2AB( 4 ’ 2) ~2’622A—"YT • 1331 -B 0 where B(a^b) :— J xa- 1(1 — x)b-1dx is the loeta, function. 1.6. Case y — 0• a G R1 If a — 0• Y — 0 then problem (3) can be reduced to ■Vм — —di u‘ (0) — u‘ (l) — 0. This problem has the following solution u (x) — C V C G R1 aiid d — 0 • and it has no solutions if d — 0. I -ZZZA tttl tttfr л V X У V 3 - 2 - о-. -I 11 te уу у\ у у у v у УХУ тг т t Л УХ V -з -2 -1 О и ^у аЛу у IU V * 4 4. у у у у у i у у бууу i*у г Дг/г 44 4 4 4ii4 1 2 3 1 - X X X X XX УУУХХУ ти У У У У У У У »>'«-♦ Z/ rtttttt 0- -I - у 4 4 ill 44/4 444444 4»/ 444 44 /* ХУУУУ -2 - -з - -з -2 -1 I УУУ Fig 6. Phase diagram for the case a > 0, y = 0 with a = 0,1 on the left and for the case a < 0, y = 0 with a = 0, 1 on the right If a > 0, y = 0, by the re-scaling u = u(/ax), problem (3) can be reduced to u ‘‘ = —u — a, u ‘ (0) = u ‘ (L) = 0, where L = /al and a = a- This problem has the following solution πk u(x) = C cos(/ax) — a, l = —=, k E Z +, C E R1. α If a < 0, y = 0, by the re-scaling u = u(/—ax), problem (3) can be reduced to u ‘‘ = u — а, u ‘ (0) = u ‘(L) = 0, (36) where L = /—a l and a = — Д This problem has the following solution u (x) = a. For convenience, we summarize our existence results in the form of Table. 1.7. Example As shown in [3], the possible dimensionless function f (u,T) at hxed T can be written Tn 232 T — T0, ^332^ CT1 ( T ) f(u,T) = 4T0(1 — u ) + a to (u + 1) + foTln I to , where T0 is a, critical tnmperature. c is the heat capacity, a = 4^0 is dimensionless. I is the latent heat, f0 is a parameter with dimensions of energy density. Comparing (37) with our f (u). we hud that T T — 2 a (T — T0) 2 a (T0 — T) 1 = To ’“ = To, ’ a = TO ’ C = cT ln (T) + T+ 4“(T — T0>. f0 T0 / 4 T0 I.В. Krasnyuk, R.M. Taranets, M. Chugunova Table Conditions on the problem’s parameters for existence and non-existence of nontrivial solutions α σ γ p L0 > 0 2 4α3 σ < 27γ > 0 p C [pmin, pmax ) Yes (2 sol’s) > 0 2 4α3 σ < 27γ > 0 p < pmin Yes > 0 2 4α3 σ < 27γ > 0 p ≥ pmax No > 0 2 4α3 σ ≥ 27γ > 0 p < pmin Yes > 0 2 4α3 σ ≥27γ > 0 p ≥ pmin No > 0 R1 < 0 p > pmin Yes > 0 R1 < 0 p ≤ pmin No > 0 R1 = 0 R1 Yes (family sol’s) < 0 R1 > 0 p > pmin Yes < 0 R1 > 0 p ≤ pmin No < 0 2 4α3 σ < 27γ < 0 p C (pmin, pmax] Yes (2 sol’s) < 0 2 4α3 σ < 27γ < 0 p > pmax Yes < 0 2 4α3 σ < 27γ < 0 p ≤ pmin No < 0 2 4α3 σ ≥27γ < 0 p > pmin Yes < 0 2 4α3 σ ≥27γ < 0 p ≤ pmin No < 0 R1 = 0 R1 No = 0 R1 > 0 p> 3 (3 )*/3 Yes = 0 R1 > 0 p < 3 (' )*/3 No = 0 R1 < 0 p> -3(3)4/3 Yes = 0 R1 < 0 p < 3 (3 )*/3 No = 0 R1 = 0 R1 No For example, if 0 < T < T0 then a > 0, y > 0, and ст > 0. In this case, according to the paragraph 2.1, problem (3) has nontrivial solutions. On the other hand, if T > T0 and a < 2(TT-T0) then a > 0, y > 0, ст < 0 and we again have the existence of nontrivial solutions.
2 . The Steady States for General Free Energy In the previous section, we have studied the case when the free energy contains the linear term but it has no cubic term. Note that the presence of a linear term breaks down the symmetry of the free energy. Next, we will examine how the length of the existence interval can be effected by the cubic term. It is possible to introduce asymmetry in a phase diagram by adding odd powers to the free energy expansion so that f (u, T ) = a 0(T) + a 1(T ) u + a 2(T )2 + a 3(T )"3 + a 4(T )^ + O (u 5) • (dS) Note that the special case a 1(T) = a3(T) = 0 was introduced in [6, p. 19, (2.41)]. The authors assumed that a4(T) > 0 and a2(T) < 0. Then f(-,T) has maximum at u = 0 and minimum at -± = ±\j-a4• By definition, it is easy to verify that f (0, T) = a0(T) > 0 and f (-±,T) < 0 as a2 > 4a0a4 > 0. It means that there is a point -0 G (0, — OJ) such that f (±-0, T) = 0. Thus, we can calculate the minimal length as L0 -u0 dt Vt—u 0)(t2-ul) V a 4 -2 / -1 dt V(i — 12)(i —"Pty’ where u0 = A----a/a2 -4a0 a4, u 1 = A /---1--Ja2 — 4a0a4 a4 a4 a4 a4 k2 -0 G (0,1). (40) u1 Substituting the new variable t = sin ф into (39), we have L = 2ПЕ [n/2 a4u21 0 dφ V1 — k2 sin2ф Next, consider the ecpiation 1 „ 2(-' )2 = R (-) then u2 L - =^j u1 dz VW) ’ vdiere -i are real roots of R(-) = 0 such that - 1 < -2. Here R (z) = az4 + bz3 + cz2 + dz + e = a (z2 + pz + q)(z2 + p z + q') (43) where a, b, c, d, e, p, q, p, q' G R, a = 0, i. e. be + (ad — bc) q . p =-------1-’ p = a(2e — cq) be - adq ′e a(2e — cq) , q = —’ q = aq 1 c i c2— 4 ae A 2 . 2 ^ ±V a^) ’ c > 4ae' Note that (43) has four real roots -1,2 = 2 (—p ± Vp2 — 4q) ’ -з,4 = 2 (—p‘ ± V(p)2 — 4q‘) provided that p2 — 4q > 0 and (p‘)2 — 4q > 0. Assume that p = p'. By change of variables ^t±V ^ — v zt + 1 ’ z (t +1)2 dt I.В. Krasnyuk, R.M. Taranets, M. Chugunova in (42), we deduce that L 0 — µu2 +ν u2 u2+1 — A / 2 J Rr)P J u1 µu1 +ν u1 +1 dt V(1 + k 112)(1 + k2t2) 1 where A — µ -ν 2 a (v2 + pv + q)(v2 + p'v + q') Here, µ k—ц2 + pц + q k—ц2 + p' ц + q' 1 v2 + pv + q ’2v2 + p' v + q' and v can be found from equations p (ц + v) + 2( q + цv) — 0, p (ц + v) + 2(q' + цv) — 0, hence v— q′ - p- q± p′ - pq′ p′ - - p′q , ц p q′ - p- q∓ p′ - pq′ p′ - p′q . -p If (43) has four real roots then ki < 0. By change of variables t — (—k 1) 1/2 sin ф in (45), we deduce that φ2 L о = Ai φ1 dφ V1 — k3 sin2ф where A — -A - =, kз — 27 > 0, фi — arcsin ( ^ 1(^ui+v)) . k i k 1 V Ui + 1 / In particular, if (43) has only two real roots then k 1 < 0 and k2> 0 оr k 1 > 0 and k2< 0. Moreover, if a > 0 then the problem has no solutions therefore we have to consider the case a < 0 only. Ass nine that k 1 < 0. Then we olot ain (48) with k 3 < 0. In the case p — p'. by change of variables z — t — p in (42). we deduce that where u2 y/2 Г dz 0 2J ^RT) u1 p u2 -2 —A u1 p dt , у a(1 — k112)(1 —Z212) z 2y/2 V( p2 — 4q)(p2 - Z ^=^, k^ — 4 q') p2 - /X >0, k 2 — 4q —--— > 0. p2— 4q' By change of variables t — (k1) 1/2 sin ф in (49), we find that φ2 L о = M φˆ1 dφ \ja (1 — k3 sin2ф) where Z k3 = У > 0, фi = arcsin f Vki(ui — p/2) ) . k1 Next, we consider the special cases p2 = 4q оr (p')2 = 4q‘. For example, if (p‘)2 = 4q‘ then -p - Vp2-4q -p + Vp2-4q ( .p')2 R(u) = --2-----) (u--2-----) Г +2j • If a < 0 then two cases are possible: (i) - p′ 2 E —p — Vp2— 4 q I 2 ’ —p + Vp2-4q 2 )’ (ii) ( -p - Уp2— 4 q —p + Уp2— 4 q 2 ) In the first case (i), we find that L0 = to. In the second case (ii), we have (48). On the other hand, if a > 0 then the problem has no solution in the case (i) but for the case (ii) we have L0 = to. In particular, if p2 = 4q arid (p‘)2 = 4q then R (u) = a (u + p)2 (u+y. Obviously, if a < 0 then the problem has no nontrivial solutions but if a > 0 then L0 = to.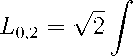
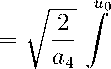
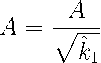
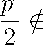
Список литературы Stationary solutions for the Cahn - Hilliard equation coupled with Neumann boundary conditions
- Cahn J.W., Hilliard J.E. Free Energy of a Nonuniform System, I. Interfacial Free Energy. The Journal of Chemical Physics, 1958, vol. 28, pp. 258-267. DOI: DOI: 10.1063/1.1744102
- Carr J., Gurtin M.E., Slemrod M. Structured Phase Transition on a Finite Interval. Archive for Rational Mechanics and Analysis, 1984, vol. 86, pp. 317-351. DOI: DOI: 10.1007/BF00280031
- Fife P.C., Penrose O. Interfaced Dynamics for Thermodinamically Consistent Phase-Field Models with Nonconcerved Order Parameter. Electronic Journal of Differential Equations, 1995, vol. 16, pp. 1-49.
- Grinfeld M., Novick-Cohen A. Counting Stationary Solutions of the Cahn -Hilliard Equation by Transversality Arguments. Proceedings of the Royal Society of Edinburgh: Section A Mathematics, 1995, vol. 125, no. 2, pp. 351-370. DOI: DOI: 10.1017/S0308210500028079
- Grinfeld M., Novick-Cohen A. The Viscous Cahn -Hilliard Equation: Morse Decomposition and Structure of the Global Attractor. Transactions of the American Mathematical Society 6, 1999, vol. 351, no. 6, pp. 2375-2406.
- Provatas N., Elder K. Phase-Field Methods in Materials Science and Engineering. Weinheim, Wiley-VCH, 2010. 312 p.
- Novick-Cohen A., Peletier L.A. Steady States of the One-Dimensional Cahn -Hilliard Equation. Proceeding of the Royal Society of Royal of Edinburg, 1993, vol. 123A, pp. 1071-1098. DOI: DOI: 10.1017/s0308210500029747
- Smoller J., Wasserman A. Global Bifurcation of Steady-State Solutions. Journal of Differential Equations, 1981, vol. 39, pp. 269-290. DOI: DOI: 10.1016/0022-0396(81)90077-2


