Статистический анализ динамики сырьевых показателей сахаропроизводящего комплекса

Прогнозирование основных показателей роста сахарной свеклы является важной задачей для осуществления эффективного управления сахаропроизводящим комплексом. Решение данной задачи позволяет предсказать не только количественные характеристики сырья, но и рационально выбрать время начала сезона производства по переработке сахарной свеклы. С учетом климатических условий России правильный выбор времени начала сезона производства является одним из важных факторов в получении максимального количества сахара [1]-[3].

Необходимо отслеживать динамику изменения двух основных показателей сахарной свеклы – средней массы свекловичного корня m кср и среднюю сахаристость корня s кср , и уметь прогнозировать их развитие с течением времени.

При построении прогнозных моделей необходимо учитывать следующие особенности:

• 1.    В ходе созревания свеклы измерение сырьевых показателей производится сырьевой лабораторией один раз в декаду.

• 2.    При построении прогнозной модели нельзя явным образом учесть все причины, влияющие на развитие сырьевых показателей.

С учетом данных особенностей наиболее оправданным будет применение статистических методов анализа временных рядов, единственным объясняющим параметром которых будет время.

Предлагается рассмотреть использование авторегрессионных и адаптивных методов прогнозирования временных рядов сырьевых показателей.

Модели прогнозирования массы и сахаристости свекловичного корня строились на реальных данных зоны свеклосеяния сахаропроизводящего комплекса Воронежской области для сезонов 2013 и 2014 годов. Рассматриваемый временной ряд значений сырьевых показателей содержал 6 значений (рисунки 1, 2).

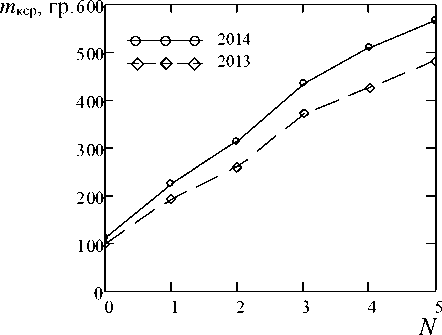
Рисунок 1. Временной ряд средней массы свекловичного корня

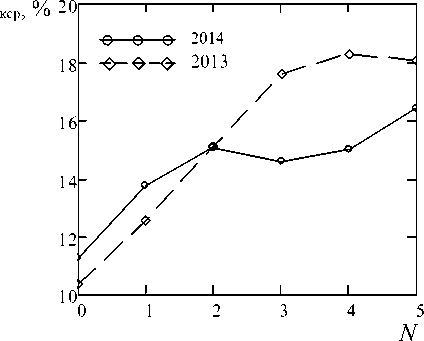
Рисунок 2. Временной ряд средней сахаристости свекловичного корня

Для построения модели авторегрессии была получена автокорреляционная функция временного ряда массы корня и сахаристости (рисунки 3, 4).

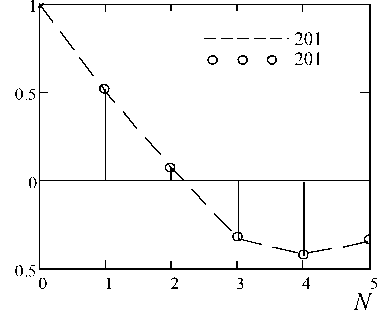
Рисунок 3. Автокорреляционные функции, соответствующие кривым роста 2013 и 2014 годов

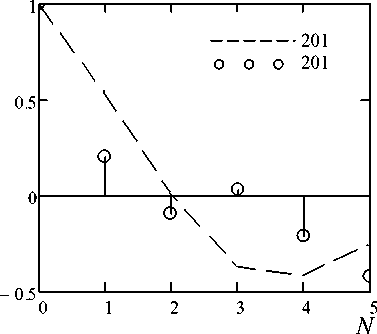
Рисунок 4. Автокорреляционные функции, соответствующие кривым роста 2013 и 2014 годов

Как видно из рисунка 1, поведение кривой роста сырьевых показателей определяется трендовой компонентой. Это также подтверждается графиком автокорреляционной функции, из которого видно, что наибольшим оказался коэффициент автокорреляции первого порядка.

Для прогнозирования сырьевых показателей были построены модели авторегрессии первого и второго порядка:

^KCp(t) = Pok + PlK^KCp(t-l);

^ KCp(t) = P ok ⁺ P lK ^ KCp(t-l) +

+ P2k^-KCp(t-2)'

Skcp(t) = Рос + P1c5KCp(t-1);

S kcp(t) = Р ос + P 1c⁵KCp(t-1) +

+ p2cSKCp(t-2)

где: ^ _KCp(_t) , S _KCp(_t) - прогнозируемые значения показателей массы свекловичного корня и сахаристости для временного значения ряда t ;

β nк , β nс – коэффициенты авторегрессии для временных рядов массы свекловичного корня и сахаристости соответственно.

Определение коэффициентов моделей авторегрессии β производилось с помощью метода наименьших квадратов [4]:

β = (XTX)-1XTY,            (5)

где X – матрица определяющих значений, Y – вектор зависимых значений. Расчёты производились с помощью математического пакета MathCAD. Результаты аппроксимации сырьевых показателей по моделям авторегрессии первого и второго порядка приведены на рисунках 5 и 6. Ниже приведены выражения с численными значениями коэффициентов, по которым производились расчеты для сезона 2013 года.

^ cp(t) = 130,782 + 0,874rn_Kcp(t - ₁₎; (6) rn_Kcp ( _t ) = 185,298 + 0,454m Kcp(t-i) +

+ 0,375mKcp(t-2);

^Kcp(t) = 8,989 + 0,429sKcp(t-i);

S Kcp(t) = 12,844 + 0,065s Kcp(t-i) +

+ 0,108sKcp(t-2);

Далее, записаны такие же выражения для сезона 2014 года.

^ Kcp(t) = 107,748 + 0,885m Kcp(t-i) ; (10) ^ Kcp(t) = 168,002 + 0,278m Kcp(t-i) +

+ 0,561m Kcp(t-2) ;       (11)

^ Kcp(t) = 5,945 + 0,702s Kcp(t-i) ; (12) ^ Kcp(t) = 6,469 + 1,159s Kcp(t-i) —

- 0,548s Kcp(t-2) .        (13)

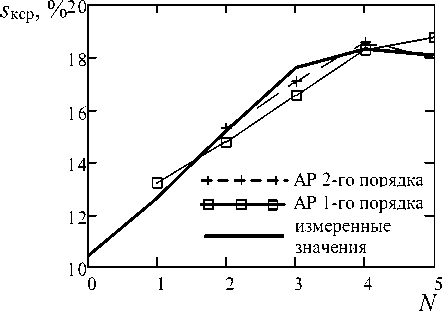
Рисунок 6. Авторегрессия 1 и 2 порядка для сахаристости. Сезон 2014 года

Авторегрессионная модель достаточно хорошо аппроксимирует кривую роста, вместе с тем существуют особенности по ее использованию в качестве прогнозной. Эти особенности проявляются в тех случаях, когда кривая роста претерпевает колебательные изменения, так, как это показано на рисунке 5. Недостаточность объема исходных данных не позволяет кривой на графике принять необходимый наклон, соответствующий истинной скорости изменения сырьевого показателя. С другой стороны, на рисунке 6 хорошо видно, что авторегрессия первого и второго порядка адекватно описывает изменение показателей. Точность прогноза будет определяться объемом измеренных данных.

С учетом более стабильного развития массы свекловичного корня, авто-регрессионная модель хорошо справляется с описанием поведения этой сырьевой характеристики (рисунки 7, 8). На графиках отображен прогноз на три точки вперед, рассчитанный с помощью авторегрессии первого и второго порядка.

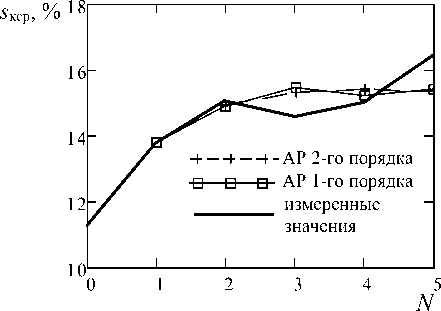
Рисунок 5. Авторегрессия 1 и 2 порядка для сахаристости. Сезон 2013 года

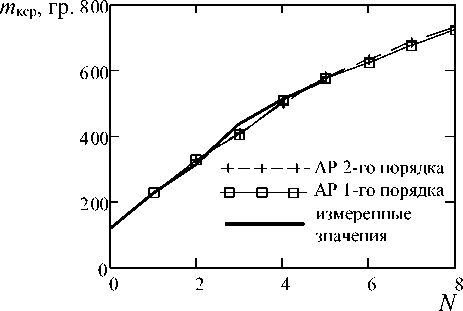
Рисунок 7. Прогноз с помощью модели авторегрессии 1 и 2 порядка массы свекловичного корня. Сезон 2013 года

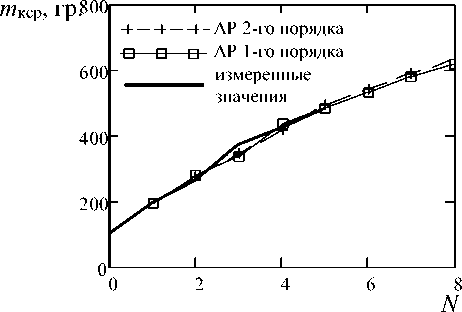
Рисунок 8. Прогноз с помощью модели авторегрессии 1 и 2 порядка массы свекловичного корня. Сезон 2014 года

Было рассмотрено построение прогноза сырьевых показателей на основе линейной модели Брауна. Эта модель относится к адаптивным моделям на основе метода скользящего среднего [5].

Суть линейного метода Брауна заключается в том, что первоначально выполняется оценка коэффициентов модели по N первым измеренным значениям, а затем, производится предсказание с учетом коэффициента γ, который определяет степень доверия к новым или предшествующим значениям. Далее происходит адаптация (поправка) коэффициентов модели с учетом разницы предсказанного и реального значения наблюдаемой величины по формулам [5]:

^a o(t) = ^a o(t-i) + ^a i(t-i) + (1 - Y²) ^e(t) , (14)

^a i(t) = ^ai(t-i) + ^{(1 -} Y^{2 )} 6 (t) , ⁽¹⁵⁾

где a o , a 1 - коэффициенты линейной модели предсказания y = a o + a 1 1 , t = 1,2, ..; e - ошибка прогноза; у — коэффициент дисконтирования данных, который определяется экспертом по серии расчетов.

Результаты расчетов по модели Брауна приведены на рисунках 9 и 10. На рисунке 9 показано сравнение прогнозных значений, выполненных для интервала адаптации длиной в три временных значения и коэффициенте дисконтирования γ = 0,7. Такая величина коэффициента свидетельствует о тесной взаимосвязи смежных измеренных значений массы свекловичного корня.

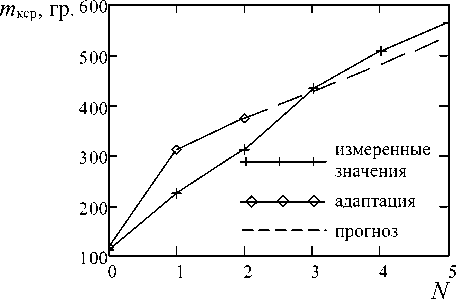
Рисунок 9. Прогноз массы свекловичного корня с помощью адаптивной модели. Сезон 2013 года

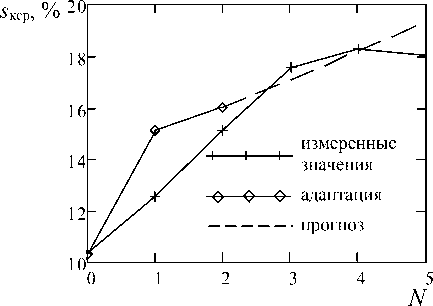
Рисунок 10. Прогноз сахаристости свекловичного корня с помощью адаптивной модели. Сезон 2014 года

На рисунке 10 показаны результаты прогнозирования сахаристости, для значений в сезоне 2014 года. Коэффициент γ = 0,7 также является пригодным для построения прогноза, как и для случая 2013 года.

Для построения прогноза сахаристости в 2013 году, коэффициент γ был определен равным 0,3, это легко объясняется поведением кривой роста (см. рисунок 2), где видно, что для правильного определения скорости увеличения сахаристости необходимо опираться на более ранние показатели.

Полученные результаты построения прогнозных моделей сырьевых показателей свидетельствуют о возможности их практического использования. Полученный результат во многом определяется навыками эксперта-прогнозиста, который должен правильно выбрать прогнозный метод, и с учетом этого определить параметры модели прогнозирования.