Стохастическая двумерная модель распространения загрязнения реки

Проблема охраны окружающей среды, а также задачи экологического мониторинга и долгосрочного прогнозирования являются важнейшими задачами науки в современном мире. Интенсивное развитие промышленности и связанное с этим увеличение промышленных выбросов, загрязняющих окружающую среду, уже стали ощутимыми для экологического равновесия многих регионов страны и мира. Промышленные выбросы приводят к угнетению жизни растительного животного мира (птиц, рыб, насекомых, полезных бактерий и др.) [1]. Проблемы окружающей среды, причинами которых является рост объема загрязнений, сбрасываемых в

(с) Полосков И. Е., 2016

Работа выполнена при частичной финансовой поддержке РФФИ (проект № 14-01-96019), а также Минобразования и пауки России (Задание № 2014/153).

естественные водные бассейны, разливы нефти требуют быстрой реакции с целью предотвращения дальнейшего ухудшения качества воды,а также загрязнения подземных вод и водоносных слоев.

В настоящее время при рассмотрении таких сложных процессов как течения, принято выделять детерминированную и вероятностную составляющие [2]. Детерминированная компонента полностью определяется гидродинамическими законами и гидрологией водоемов; вероятностная составляющая является результатом наложения случайных факторов и может быть оценена лишь путем статистической обработки массового материала наблюдений. При этом стохастические модели уже давно являются рабочим инструментом в задачах гидрологии [2-7].

При стационарном протекании транзитного потока струя загрязненной жидкости, поступая в него, распространяется по течению, постоянно перемешиваясь и разбавляясь в результате турбулентной диффузии [2]. Характерной особенностью турбулент- ных движений является наличие пульсации гидродинамических величин потока, которые по своей природе являются беспорядочными [1]. Важной задачей является оценка вероятностных характеристик потока, которая может быть получена при использовании различных моделей переноса загрязнений и, в том числе, с учетом запаздывания и наличия распределенных параметров.

• 1.    Постановка задачи

Рассмотрим следующую модель распространения попавшего в реку загрязнения:

dU ( x,y,t' ) ∂t

+1 ui+*1 Vi(t) ] ^{dU (} д_x ^y ^t ⁾ +

+ [ U2 + *₂ V>(t) ] ^W( X'y't ¹ = ∂y

= V1

d²U ( x,y,t) +    d²U ( x,y,t )

∂x2        2 ∂y2

-

- [ c + *3 V3(t)] U ( x,y,t ) , (1.1)

U ^(x,У^{, 0)} = U ^2(x,y^),         (1.2)

где U(x, y,t) > 0 - концентрация загрязняю-пщх веществ в точке (х, у) в момент времени t; ui, U2, vi, V2, c ~ положительные постоянные, представляющие собой неслучайные средние продольную и поперечную скорости водного потока, коэффициенты продольной и поперечной диффузии и консервативности вещества. Как и в других моделях, считаем, что для случайного поля U2(x,y) известны все необходимые числовые характеристики. Влияние случайных факторов в уравнении модели отражено присутствием слагаемых *1 Vi(t). *2 V2(t) 11 *3 V3(t). Г,де Vi(t) - независимые белые шумы с нулевыми средними и единичными интенсивностями, *i = const, дает массу загрязняющих веществ в момент времени t.

Основная задача исследования в данной работе состоит в построении и решении уравнений для функций mi(x,y,t) = E[U(x,y,t)\ , m2(xi,yi,x2,y2,t) =

= E [ U ( xi,yi,t ) U ( x2,y2,t )]

• - первых моментов концентрации, если известны значения этих функций в начальный момент времени

• 2.    Уравнения для первых моментов

mi(x,y) = E [U0(x,y)] = mi(x,y, 0), m2(xi,yi,x2,y2) =

= E [ U² ( xi,yi ) U0 ( x2,y2 ) ] =

= m2(xi,yi,x2,y2, 0), где E[...\ - символ математического ожидания .

Для вывода искомых уравнений воспользуемся схемой перехода от непрерывной к дискретной среде и обратно [8]. Для этого в области D = { ( x,y ) | x G R, 0 <  у <  L} (формально выберем сетку {xq,yr }: xq = qhx- yr = rhy- q = о. ±1. ±2..... r = 0.

• 1.    2..... N (hy = L/N) ii дискретизиру

ем уравнение (1.1) по переменным x и у, заменяя частные производные функции с их конечно-разностными аппроксимациями. В результате получим бесконечную систему стохастических дифференциальных уравнений (СДУ) для счетного числа случайных функции Uq_r ( t ) е белыми шумами Vi ( t ) ii = 1 , 2 , 3) на входе (метод прямых)

^Uqr = ^—[ ^{c +} *3 ^V3^(t) ] ^Uqr ^—

Uq +1 ,r ^- Uq - 1 ,r ^— (ui + *i Vi ^{(t )}) -----—--

2 h_x

Uq,r +1 ^- Uq,r - 1

• — U2 + *2 V2 ( t)\ -----—--+

2 hy

+ v i

^Uq+i,r ^{— 2 U}qr ^{+ U}q - i,r h ² _x

+

Uq,r +1

+ V2—--

^{— 2} Uqr ⁺ Uq,r - i

hy ²

(2.1)

Используя формулы Стратоновича [9], с учетом формулировки рассматриваемой проблемы и вида коэффициентов сноса и диффузии

-

c m 1 qr

-

u 1

m 1 ,q +1 ,r

-

m 1 ,q - 1 ,r

2 hx

-

-

a qr

N - 1 3

— fqr +2еее

i

j =1 k =1

-

bqrsp —

k =1

где

fqr —

-cuqr

^^^^^^^^г

∂g qrk

∂u ij

g ijk ^,

(2.2)

u 2

mi,q,r+1 - mi,q,r - 1

2 hy

+ V1 mA q+V

-

g qrk g spk ,

(2.3)

m 1 ,q,r +1

+ Vy-------

-

2 miqr + mi,q - 1,r h ² _x

2 miqr + U1,q,r - 1 ^hy ²

+

+

-U1

u q +1 ,r

^^^^^^^^г

u q - 1 ,r

2 hx

^^^^^г

u2

u q,r +1

^^^^^^^^г

u q,r - 1

2 hy

+

g qr 2 —

+ V1

u q +1 ,r

+ V2

^^^^^г

2 uqr

_h 2 _x

u q,r +1

gqrl —

^^^^^г

σ2

^^^^^г

-^i

u q,r +1

^^^^^v

+ ^uq - 1,r

+

² uqr + uqr - i

hy ²

,

u q +1 ,r

^^^^^г

u q - 1 ,r

2 hx

u q,r - 1

2 hy

,

,

gqr3 ^—

^^^^^г

σ3 u qr ^,

можно построить уравнение Фоккера-План-ка-Колмогорова (ФПК-уравнение) для совместной плотности вероятности p ( {Uq_r},t ) распределения случайных функций U_qr (t) следующего вида:

dP _— 1 V NT dt 2 2^ 2^

q,s r,p =1

∂ ² bqrsp p

∂uqr ∂usp

-

, ¹ ( ,2 mi,q+2,r

⁺ ф °i-----

2 m 1 ,q,r +2

⁺ ^ 2-------

-

2 miqr + mi,q - 2,r

-

4 h ^y _x

2 m i qr + m i ,q,r - y

⁴ hy

+

+

+ ^3 miqr ).

Переходя от дискретной схемы к непрерыв. ной, получаем уравнение для математического ожидания поля U ( x,y,t):

dmi ( x,y,t )

∂t

-

u 1

∂ ²

^{+ A}1 --

— Ao mi ( x,y,t )

dmi ( x,y,t )

∂x

^; mi ( x,y,t )

∂x ²

-

u 2

-

dmi ( x,y,t )

∂ ²

+ Ay —

∂y mi(x, y, t)

∂y ²

+

, (2.6)

^A o ^—

σ ²

— - c

2        ’

N - 1

- V V

∂ aqr p ∂uqr

(2.4)

Р ( {u..}, 0) — p 0 ( {u.} ) .

(2.5)

Заметим, что задавать начальную плотность p0 ( {u..} ) в применяемой, как и в общей [8], схеме исследования нет необходимости, так как ФПК-уравнение используется только как промежуточный инструмент получения уравнений для моментов.

Для построения уравнений относительно математических ожиданий miqr ( t ) — (U_qr ( t ) случайны.с функций U_qr ( t ) восполь зуемся аналогом формулы [9, с. 100]:

+ ∞ + ∞

m 1 qr

...

aqr

p^{( {} u.. ^{} ,t) d {}u .. ^{} —}

-∞ -∞

^A i ^{— v} i ⁺ “2 1 , m i ( x, y, 0)

Ay — V2 +

^— mi^(x,y⁾,

^σ 2 ²

2 ,

(2.7)

mi ( -w,y,t ) — mi (+ w,y,t ) — 0 ,

dm1 ( x, 0 ,t )     dm1 ( x,L,t )

∂y

∂y

= 0 .

(2.8)

(2.9)

Для вывода уравнения для начальных смешанных моментов

m2qrsp ( t ) — (Uqr ( t ) Usp ( t ) ) применим аналог формулы [9, стр. 100]:

+ ∞ + ∞

m y qrsp —

...

(aqr

usp

+ a_sp

uqr +

-∞ -∞

⁺ bqrsp ) ^{p( { u}.. ^{} ,t) d { u}.. ^{} —} Ii ⁺ I2 ⁺ I3,

^m2,q+i,rsp   ^m2,q - i,rsp

Ii —  cm2qrsp  ui          „ ,

2 hxi

- u2

m2 q,r +1 ,sp ^- m2 q,r - 1 ,sp

2 hyi

+

где у = 2 (а2 — с), а начальное и краевые

m2 ,q +1 ,rsp

+ ^v i---------

-

2 m2qrsp + m2,q-1,rsp , + hx1

условия примут форму

m2 q,r +1 ,sp

+ V2--------

-

2 m2qrsp + u2q,r-1,sp , + hy1

т2 ( Х1,У1,Х2,У2, 0) =

= m2 ( xi,yi,X2,y2 ) , (2.11)

1    2 ^m2,q+2,rsp

+ 2 Щ-----

-

^{2 m}2qrsp + ^m2,q - 2,rsp +

⁴ hX1

2 m2 q,r +2 ,sp

+ ^2 --------

-

^{2 m}2qrsp + ^m2q,r - 2,sp

^hS       +

+ CT2 m2qrsp j ,

m2(xi,yi,X2,y2,t)\        = x1=±∞

= m2(xi,yi,X2,y2,t) \         =0, (2.12)

x 2 = ±∞

I2 = - cm2q

rsp

-

+ V1

-

u1

-

m2 qr,s +1 ,p

u2

-

m2 qr,s - 1 ,p

2 hx2

-

m2 qrs,p +1

m2 qr,s +1 ,p

-

-

m2 qrs,p - 1

2 h y 2

+

^{2 m}2qrsp + ^mqr,s - 1,p

2 h _{x 2}

+

+ V2

m2 qrs,p +1

-

^{2 m}2qrsp + ^u2qrs,p - 1

h ² y 2

+

⁺ 2

2 m2 qr,s +2 ,p σ1

-

^{2 m}2qrsp + ^m2qr,s - 2,p

^{4 h} x 2

+

2 m2 qrs,p +2

⁺ ^2 --------

-

^{2 m}2qrsp + ^m2qrs,p - 2

^{4 h}y2

+

+ O3 m2qrsp ^ ,

I3 =

= ^a1

E

U q +1 ,r

-

U q - 1

2 h x i

,r

U s +1 ,p

-

U s - 1 ,p

2 hx2

]+

+ ^2 E[

U q,r +1

-

U q,r - 1

U s,p +1

-

U s,p - 1

2 h y 1

2 h y 2

+

⁺ CT3 m2qrsp.

Тогда уравнение для непрерывной среды будет иметь следующий вид:

∂m2

~tr = ^m ^{2 -}

-

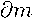
ui( ---2 +

∂m2       ∂m2 ∂m2

∂x2 ^{u 2} ∂y1 ∂y2

+ , J^ + 2 J^ + ¹ ∂x1 ∂x2     ² ∂y1 ∂y2

∂ ² m2   ∂ ² m2

^{+ A1}( ~вл~ ⁺ 'dxr Г

+A 2 (^+^dd_?), _Ш(1)

dm2(xi,yi,X2,y2,t) I dyi          \yi=0L

dm2 ( xi,yi,X2,y2,t ) I        = 0

dy2            \ y2=0,L

(2-13)

Полученные уравнения (2.6)-(2.13) представляют собой замкнутую систему детерминированных уравнений в частных производных относительно математического ожидания и второго начального смешанного момента случайного поля концентрации загрязнения.

3. Решение уравнений

Заметим, что линейные дифференциальные уравнения в частных производных (2.6) и (2.10) для первого и второго моментов разделились, имеют постоянные коэффициенты и, по крайней мере в частных случаях, могут быть решены точно.

Рассмотрим далее такой частный случай, а именно, предположим, что U2 = СТ2 = 0. Этот случай соответствует отсутствию наблюдаемого течения в реке в поперечном направлении. При U2 = а2 = 0 (A2 = V2) уравнение (2.6) примет следующую форму:

dmi ( x,y,t )

∂t

= Ao mi ( x,y,t ) — ui -------+

^{+ A} i

d ² mi ( x,y,t )

∂x ²

+ A2

d ² mi ( x,y,t )

∂y ²

(3.1)

Решение уравнения (3.1) будем искать в виде

ao ^(x,t) .

mi ^(x, y ^,t) = —2—⁺

+∞

+ '^ak ( x,t )

k=1

πk y L

(3.2)

Обратимся теперь к уравнению (2.10). С учетом U2 = а2 = 0 это уравнение будет иметь следующую форму:

Для определения функций ao, a1, а₂, ... подставим ряд (3.2) в указанное уравнение и приравняем коэффициенты при косинусах с одинаковыми аргументами, что позволяет записать следующие уравнения для искомых коэффициентов:

dao(x,t)

---dt--- = Ao ao ( x,t )

∂m		u 1	∂m 2	∂m 2 dx- ) +
- = ∂t	µ m 2 -		+ ∂x 1
2	∂ 2 m 2	+ Ai	/ d2m2 ∂x 2 1	∂ 2 m 2
+ ai	∂x 1 ∂x 2			1 dx-
	+ A- /		d2m2   d2m2 \ ∂y 12      ∂y 2 2

)+

. (3.7)

dao ( x,t )

-

+ A1

d²ao(x, t ) ∂x²

(3.3)

dak ( x,t )                     dak ( x,t ,

---dt ---= ^Ao ak^{(x,t) —} ui — dX --⁺

+ ^1 d²ak ( x ,t)

- A2 ( L ) ak(X’t)’ k = 1, 2,... (3.4)

Решение (3.3) имеет вид

^a o ⁼

+∞

У Hi ( x,t ; z ) ^10(z) dz,

(3.5)

-∞

где

H_i(x, t ; z) =

Решение этого уравнения с условиями

(2.11)-(2.13) будем искать в виде

a 00( x i , x 2 , t )

m2 ( xi,yi,X2,y2,t ) =------4--+

• 1    +^                nky_i

• +    2 2^a^m ( xi,X2,t ) cos ——+

k =1

+∞

1 v^               nsy₂

• ⁺    2 2^aois ( xi,X2,t ) cos ——+

s =1

+∞

πk y 1     πs y 2

• +     aiiks(Xi,X2,t) cos —— cos ——.

LL k,s =1

(3.8)

2 Дпсз t

exp c11 —

( x - z - c 2 t )² 4 ПС3 t

,

Для того чтобы найти коэффициенты aoo- aiok- aois- aiiks- подставим правую паств равенства (3.8) в уравнение (3.7) и приравняем коэффициенты при косинусах с одинаковыми аргументами, что ведет к следующим уравнениям для искомых коэффициентов ( k,s = 1, 2, ...):

Eio(z)

L

L J mi ( z,y ) dy, 0

ci = ^AO,     c2 = ui,      c3 = ^A1.

∂a 00 ∂t	∂a 00 = ц aoo  “i   dx	daoo \ + dx-
+ ^-	d^ + Ai ( ^	'■+^ \ ^

Подобным образом можно получить и решения уравнений (3.4):

∂a 10 k                 ∂a 10 k   ∂a 10 k

— = ^“^{iok —} “4 dx^ ⁺ J+

ak =

+∞

У Hi ( x,t ; z ) Eik (z) dz,

(3.6)

2 ∂ ² a 10 k

+ ^i

∂x 1 ∂x 2

∂ ² a 10 k ∂ ² a 10 k

^{+ A}M “axT ⁺ ~Xh=r)

-

-∞

где

πk ²

^{— A}2 [^ L) aiok , (3.10)

L

Eik^(z) = LL У mi ( z,y )

cos nkydy, L

Ci = A₀ — A2 (L^ )2.

c2 = ui,   c3 = ^A1.

∂a 01 s ∂t	= ^aoik — “i	/ daois + daois \ ∂x 1      ∂x 2	+
+ ^i2	d2aois + A ∂x 1 ∂x 2    1	/ d2aois + d2aois ∂x 21       ∂x 2 2	)—
	^^^	\ ( ns ^2 λ 2 L     a 01s ,	(3.11)

∂a11ks dt  = yaiiks

^^^^^.

∂a11ks   ∂a11ks up— + -ххг г

,   2 d²a_nks +

¹ ∂x 1 ∂x 2

∂ ² a 11 ks ∂ ² a 11 ks

⁺ М “aXf ⁺ ~мГ)

X ^2iiks(zi, z2) dzi dz2, (3.16) где

^2i0k ( zi,z2 )

^^^^^.

π ²

- ^A2 Ly) ^ k ⁺ s ^ allks- (3-12)

_ 4

= L2

LL

J J ^m2^(zi^,yi^,z2^,y2^{) x}

Решение уравнения (3.9) имеет вид

πk y 1

x cos —-— dyi dy2, L

+∞ +∞ аоо = / / H2(xi,X2,t; Z1,Z2)x

-∞-∞

X ^2oo(zi, Z2) dzi dz2, (3-13)

^20is ( zi,z2 )

_ 4

= L2

LL

J J ^m2^(zi^,yi^,z2^,y2 ) ^x

где

H2 ( xi,X2,t ; Z1, Z2 ) =

πs y 2

x cos —— dyi dy2, L

=------;--- exp c t

2 nt y/\K\       ¹

2 x ^T K ¹ x ),

^2iiks ( zi ,z2 ) =

LL

x = {xi - zi - C2 t, X2 - Z2 - C2 t}^T,

K =f: c] ■

= L2 J J m2^^zyyz^z2,y-2) ^x

πk y 1     πs y 2

x cos —-— cos —-— dy_i dy₂, LL

^2Oo ( zi,z2 ) =

LL

= L2 У ym0(zi,yi,Z2,y2) dyi dy2, ci = У, C2 = Ul, C3 = ^1, C4 = Al, где t - символ транспонирования.

Используя то же ядро H₂ ( x_i,x₂,t ; z_i,z₂), можно получить и решения уравнений (3.10)-(3.12):

причем для aiok- aoik- aiik кочетлиты C2- C3. C4 те же. Ч'то ч для aoo- а ci равна соответственно

У - A2 ( L )², У - A2 ( L )²,

У ^{- A}2 ( L ) ( к² + s² ).

Итак, решение поставленной задачи получено в терминах соотношений (3.2), (3.5), (3.2), (3.8), (3.13) (3.16).

a i0 k =

+∞ +∞

У У H2 ( xi,x2,t ; Zi,Z2 ) x

-∞-∞

X ^2i0k ( zi, Z2 ) dzi dz2, (3.14)

a 0i s =

+∞ +∞

У У H2 ( xi,x2,t ; zi,z2 ) x

-∞-∞

X ^20is(zi, z2) dzi dz2, (3.15)

Заключение

В работе сначала построены, а затем в приближенно аналитической форме получены решения уравнений для первого и второго моментов случайного поля загрязнения, распространяющегося по течению реки. Схема решения основана на применении функций Грина и разложений в ряды Фурье по косинусам.

+∞ +∞ aiiks =У У H2(xi, x2, t; zi, z2)x

-∞-∞