Стохастическая модель процесса гомогенизации молока с использованием цепи Маркова

DOI:

For cite

Процесс гомогенизации молока и жидких молочных продуктов используется для увеличения дисперсности жировой фазы, что позволяет исключить отстаивание жира во время хранения молока, замедляет окислительные процессы, дестабилизацию и подсбивание при интенсивном перемешивании и транспортировании. Под степенью гомогенизации понимают средний размер жировых шариков, степень устойчивой во времени однородности (гомогенности) в смысле отсутствия микроконцентрационных неоднородностей, образующихся при смешивании взаимно-нерастворимых веществ [1]. Также размер жировых шариков в сливках оказывает существенное влияние на процесс маслообразования и степень использования жира.

Для управления процессами гомогенизации молока необходимы математические модели процессов гомогенизации, которые связывают управляющие параметры с показателями качества процесса гомогенизации. В качестве управляющих параметров используются режимные параметры технологического процесса производства молока (расход, температура молока и т.д.) и конструктивные особенности оборудования (давление в гомогенизаторе, геометрия щелей гомогенизирующих головок и т.д.). Таким образом, использующиеся сегодня математические модели описывают связь гидродинамических режимов в зоне диспергирования со средней степенью гомогенизации на базе основных теорий диспергирования [2]. Эти модели дают возможность рассчитывать параметры оборудования, обеспечивающего оптимальные скорости потоков гомогенизируемой среды и соответствующих давлений в гомогенизаторах для достижения заданной степени гомогенизации [3, 4].

Не всегда связь между основными управляющими параметрами процесса гомогенизации и качеством осуществления этого процесса поддается корректной формализации. Иногда дополнительно требуется оценка массового или объемного распределения частиц в объёме исследуемой пробы, так как степень гомогенизации оценивает размер всех частиц в среднем и не всегда выявля- ет содержание малых концентраций крупных частиц в эмульсии, а также другие неоднородности.

В случае моделирования массового или объёмного распределения и сложной структуры связи с конструкцией один из возможных вариантов -использование стохастических моделей, основанных на предположении о вероятностях перехода жировых шариков из одной фракции в другую, характеризующихся некоторыми феноменологическими коэффициентами. В рамках таких моделей особый интерес представляют модели процесса на основе цепей Маркова [5]. Процесс гомогенизации в таком случае рассматривается как переход жировых шариков из одного состояния (нахождение в определенной фракции массового или объемного распределения) в другие (фракции, соответствующие меньшей массе или объему) .

Исходя из сказанного, предлагается следующая модель процесса гомогенизации. Под действием внешних факторов система может переходить из одного состояния в другое. Система принимает состояния, которые ассоциируются с количеством жировых шариков, соответствующих определенной массовой или объемной фракции. Дискретное конечное множество состояний в соответствии с принятой шкалой описывается множеством состояний в виде сл еду ющего множества X = { x 1 ,x 2 ,...,x,,...,x_N } , i = 1, N , где x -числовой диапазон количества жировых шариков в г -ой фракции.

При синтезе структуры модели приняты следующие допущения: процесс гомогенизации носит последовательный характер; интенсивность перехода из одного состояния в другое отражает интенсивность процесса гомогенизации и характеризуется величиной X ц , а скорость изменения вероятности обратного перехода равна нулю; процесс гомогенизации моделируется переходом из состояния Xi в X j , где j>i , при этом интенсивностью переходов X ,д пренебрегаем; состояние сист ем ы характеризуется вероятностью Р г , где i = 1, N , где N - количество фракций. При принятых допущениях граф состояний представлен на рисунке 1.

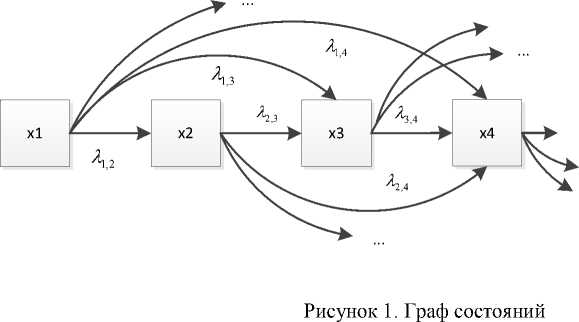
Таким образом, математическая модель процесса гомогенизации примет вид:

• —1^ = - ( ¹ + ^{1 +} ... ^{+ 1} 1, n ⁺ ... ^{+ 1} 1, n ) P ^{( p ) ;}

dp \ ,         ,                -                , / dP-p-=1,2 P( p)- dp

• ^- ( ^ 2,3 + Л 24 + ... + Я 2, n + ... + Я 2, n ) P ^{( p} ) ^;

dPdPp^ = 1 1, P ( p ) + 1 2, n P 2 ( p ) + ... + A ,- I, n P n - I ( p )

- ( ¹ , n + 1 ^{+ 1} , n + 2 ⁺ ... ^{+ 1} , N ) P n ^{( p ) ;}

-

dPdpp ) = 1 1, n P ( p ) + 1 2, n P 2 ( p ) + ... + A n , N P ( p ) + ...

⁺ 4 - 1, n^pn - 1 ( p ) ;

P ( 0 ) = P 0 , P 2 ( 0 ) = P 2,0 ,...,

P n ( 0 ) = P n ,0 ,..., P n ( 0 ) = P n ,0 ;

1,^ 0, i = 1 N , j = 1, N .

где p – давление гомогенизации.

Пусть плотности потоков 1 j постоянны, тогда, задаваясь матрицей интенсивностей прямых переходов λ и вероятностей состояний P :

Тогда решение получим в виде: N

^P ( p ) = exp⁽ p ^{L )} = Z P k ■ exp⁽ p ■ ^a k ) • P k , p > ⁰,⁽⁵⁾ k = 1

где a _k , p _k - собственные числа и вектора матрицы L , а вк - строки обратной матрицы L ^{- 1} .

Математическая модель реализована в интерактивной графической среде MathWorks Simulink™ [6]. Преобразование системы дифференциальных уравнений в структурную Simulink™ модель осуществлялось по методике, представленной в [7].

Для идентификации параметров модели использовались экспериментальные образцы молока, в которых изменение распределения жировых шариков осуществлялось гомогенизацией исходного образца на лабораторной установке гомогенизации научно-производственной лаборатории группы компаний «ЭФКО». Для исследований использовались давления 30, 60, 90, 120, 150, 180 МПа. Полученные после гомогенизации пробы исследовались с помощью цифрового микроскопа с увеличениями 100, 400, 600 крат. Параллельно делалось по 2 снимка, ввиду чего общее количество снимков составило 42 штуки. Пример микроснимка пробы молока представлен на рисунке 2.

С ¹ , ]-

- Z 1 , k k = 2

A ,2

!1^ n

_ A , N

P 2

.

.

.

... 0

■ Z 1 2, k

¹ 2, n

¹ 2, N

.

.

.

... 0

.

.

.

...

...

...

,(2)

[ P i ] =

... P n

...

,

N

^- Z ¹

... 0

¹ n , N

в матричном виде модель примет вид:

d P = L " ^P ,^P| dp

\ p = 0 = ^P 0 ,

N

где ^Л = (^Л 1 , ^Л 2,. .., ^л N ) T , Л i = Z ¹ j = i + 1

, j ,

X = ( 1 , j ) , i = 1, N , j = 1, N , L = ( X - diag ( Л ))

-

генератор цепи Маркова.

Рисунок 2. Микроснимок пробы молока

Для обработки микроснимков молока использовалось специальное программное обеспечение, которое для каждого снимка осуществляет последовательные преобразования с целью распознавания жировых шариков на снимках и расчет их геометрических параметров (площади), позволяющих рассчитать затем объем или массу, допуская сферическую форму шарика и соот(в3е)т-ствующую плотность [8, 9]. Распознанные на изображениях объекты классифицировались и распределялись по фракциям. Затем строились гистограммы распределения жировой фазы по площади проекции шарика на плоскость снимка, массе или объему. Результаты классификации по шести фракциям представлены в таблице 1.

Т а б л и ц а 1

Количество жировых шариков во фракциях

Номер фракции	Фракция, площадь, мкм2	Негом. молоко	30МПа	60МПа	90МПа	120МПа	150МПа	180МПа
P 6	3,5 : 79,5	306	656	1306	1441	2974	4195	3725
P 5	41,5 : 79,5	67	98	86	74	86	94	63
P 4	79,5 : 117,5	32	36	20	9	8	6	0
P 3	117,5 : 155,5	12	9	5	3	0	0	0
P 2	155,5 : 193,5	5	2	0	0	0	0	0
P 1	193,5 : 232	2	0	0	0	0	0	0

Для корректного использования аппарата сетей Маркова были нормированы, исходя из условия:

N

E p ( p ) = i,          (6)

=1

где N – количество фракций.

Для этого необходимо введение дополнительного коэффициента нормировки kнорм , для каждого образца, обеспечивающего выполнение равенства (6):

норм N

E p (p)

= 1

Нормированные значения представлены в таблице 2.

на который умножаются значения таблицы 1

Нормированные доли шариков во фракциях

Т а б л и ц а 2

Номер фракции	Фракция, площадь, мкм2	Негом. молоко	30МПа	60МПа	90МПа	120МПа	150МПа	180МПа
P 6	3,5 : 79,5	0,721698	0,818976	0,921665	0,94368	0,969361	0,976717	0,983369
P 5	41,5 : 79,5	0,158019	0,122347	0,060692	0,048461	0,028031	0,021886	0,016631
P 4	79,5 : 117,5	0,075472	0,044944	0,014114	0,005894	0,002608	0,001397	0
P 3	117,5 : 155,5	0,028302	0,011236	0,003529	0,001965	0	0	0
P 2	155,5 : 193,5	0,011792	0,002497	0	0	0	0	0
P 1	193,5 : 232	0,004717	0	0	0	0	0	0
коэффициент нормировки		0,002358	0,001248	0,000706	0,000655	0,000326	0,000233	0,000264

Для поиска значений параметров минимизировалось среднеквадратичное отклонение расчетных данных от экспериментальных по каждой фракции:

MN ₂

5 = EE ( j P.) эксп - j P.) рас" ) —— min,(8) j = 1 . = 1

где M , N – количество фракций и точек контроля при заданном давлении гомогенизации соответственно.

Для минимизации критерия (8) использовался метод оптимизации Pattern Search с методом поиска Latin Hypercube из библиотеки Global Optimization Toolbox MathWorks™. Результаты математического моделирования распределений представлены на рисунках 3, 4 и таблице 3. Погрешность расчетов составила в среднем по всем фракциям 0,88 % (относительной доли единицы), максимальная относительная погрешность составила 3,7% при давлении гомогенизации 30 МПа, что, видимо, обусловлено очень резким изменением свойств молока от первоначального по фракционному составу в начале процесса гомогенизации и отсутствием экспериментальных данных при давлениях гомогенизации ниже 30 МПа.

долевое распределение жировых шариков, 90 МПа

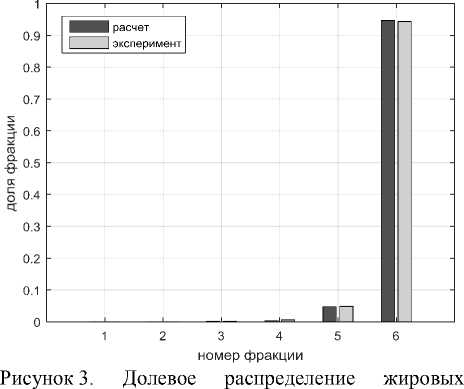
шариков, 90 МПа

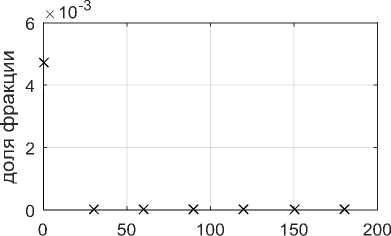
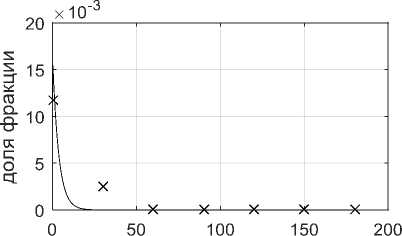
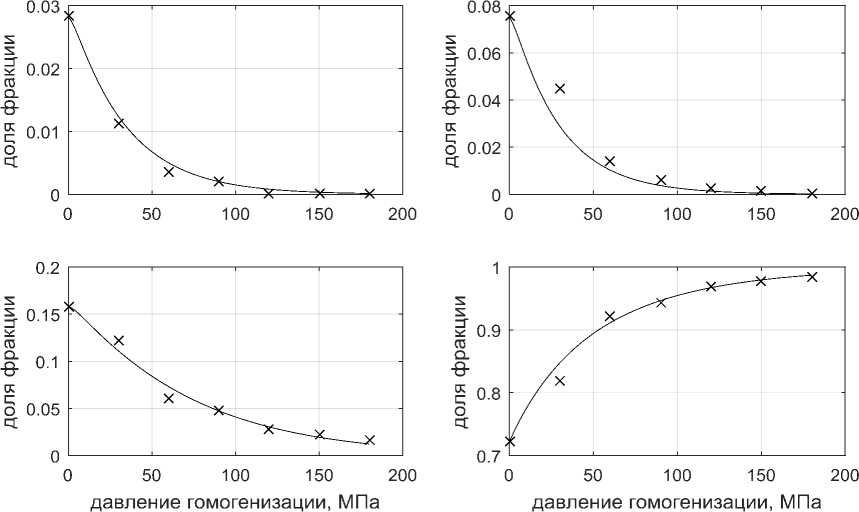
Рисунок 4. Результаты математического моделирования распределений

Рисунок 5. Р аспределение массовых долей фракций жировых шариков как функция давления гомогенизации

Т а б л и ц а 3

Параметры математической модели

Параметр	Значение	Параметр	Значение
λ 1,2	1,0486 ⋅ 107	λ 2,4	0,027566
λ 1,3	79,575	λ 3,4	0,013467
λ 1,4	1,9661 ⋅ 105	λ 1,5	0,051985
λ 2,3	0,036654	λ 1,6	0,00012538
λ 2,5	0,033678	λ 4,5	0,0026074
λ 2,6	0,042411	λ 4,6	0,039152
λ 3,5	0,012001	λ 5,6	0,013208
λ 3,6	0,0083473

Разработанная математическая модель позволяет оценить распределение массовых долей фракций жировых шариков как функцию давления гомогенизации (рисунок 5),

что дает более детальное представление о ходе процесса гомогенизации. При репрезентативном наборе экспериментальных данных параметры модели будут характеризовать интенсивность процесса разрушения конкретной фракции жировых шариков, что позволит более глубоко изучить особенность функцио- нирования технологического оборудования и проводить целенаправленное усовершенствование его конструкции и повышение его эффективности. Например, выяснить, как изменение конструктива влияет на разрушение каждой из фракций.