Structural parametric modelling of an information-analytical system
Бесплатный доступ
We develop a method for studying relations between interior and exterior characteristics of an information-analytical system. As interior characteristics, we use the balance estimates accounting for conflict interactions among the elements. We solve the problem on assuming that the interior and exterior characteristics of the system are related. We justify the expediency of using the least squares method to find an explicit functional dependence among the characteristics. We develop a method for calculating the functional dependence in the case of a matrix representation of the values of characteristics basing on pseudoinverse matrices. A numerical example illustrates how the proposed method works in the structure parametric modeling of an information-analytical system in an internal affairs department.
Information-analytical system, exterior and interior characteristics, balance estimates, least squares method
Короткий адрес: https://sciup.org/147159348
IDR: 147159348 | УДК: 519.8 | DOI: 10.14529/mmp160108
Текст научной статьи Structural parametric modelling of an information-analytical system
The operation and development of every organization require data collection, processing, and analysis. Modern information technology enables us to integrate this processes into one information-analytical system [1]. The design of this system, as well as its study and constant improvement, are possible with the use of mathematical modelling [2]. Assessing an information-analytical system (IAS) from the viewpoint of its inclusion into the organization itself, we must invariably conclude that it is necessary to consider both the variants of construction of the system and interior processes aiming at their optimization and the effectiveness of its application to management decisions.
Modelling the work of IAS and analyzing the variants of construction, which includes estimating the conflictness of the system, enable us to gather some empirical material and statistics [3]. The introduction, calculation, and study of exterior characteristics of the IAS (for instance, responsiveness, validity, accuracy, cost, and so on), whose collection depends primarily on the organization’s tasks, makes it possible to establish relations between interior and exterior characteristics.
IAS is a complicated system, important for the organization. This raises the problem of developing a balanced system possessing the desired exterior characteristics.
1. Formalization of the Prediction Problem
The approaches to estimating the interior states of the IAS as a system with elements in various relations (conflict, cooperation, and indifference) [4, 5] enables us to give comprehensive estimates based on the theory of conflicts. As estimates for the interior states of the IAS, [3] proposed to use the following seven characteristics of its elements:
M estimates how balanced the element is;
D k is the length of the shortest cycle containing the element;
S k is the length of the longest cycle containing the element;
V nm is the minimal weight of the cycles containing the element;
V nax is the maximal weight of the cycles containing the element;
B k is the minimal duration of the cycles containing the element;
M k is the maximal duration of the cycles containing the element.
Since for each element of the system we mean to calculate all seven characteristics, while the number n of elements of the system is determined only by the study goals, matrices provide a convenient representation. Denote by the matrix B^ of size 7 x n the collection of values of the interior characteristics of the i th variant of the system, for i = 1 , 2 ,... ,r.
In general, for exterior estimates we can use k characteristics. Denote by the matrix V ( i ) of size 1 xk the collection of exterior characteristics of the i th variant of the system. We should note that the calculation of exterior characteristics for each variant of the system can be a very laborious procedure requiring the involvement of a community of experts, as well as long processing and analysis of the results. For this reason, the number of variants under consideration is limited.
Thus, we can obtain two collections of characteristics (interior and exterior) corresponding to each inspected variant of the system:
{B^, V^),
(B^.
F^
).
On assuming that it is possible to determine and formalize the correspondence between interior and exterior characteristics, we can state the following problems:
Problem 1.
Given the desired exterior characteristics
V
des, define the values of interior characteristics and make conclusions on the possibility of constructing the corresponding variant (
r
+ 1) of the system.
Find
V
(
r
+1) :
E(BU n,V
(
r
+1)
) Л (V
(
r
+1) =
V
des
).
Problem 2. Given balanced values of interior characteristics Bdes, determine whether the variant under consideration satisfies the requirements of the exterior characteristics fold B(r+1) : 3(B(r+1),V(r+1)) Л (B(r+1) = Bdes).
2. Justification of a Method for Finding a Functional Dependence between the Characteristics The inspected variants of the system amount to a sample of observations in the collection of all possible variants; consequently, in order to solve the above problems, we can use one of the methods of applied statistics [6]. The main methods for constructing statistical estimates are: - the maximal likelihood method; - the method of moments; - the least squares method; - the method with weighted observations.
As applies to our problem, we can note that the maximal likelihood method has good properties (consistency, unbiasedness, efficiency) only for large samples, and so we cannot use it because
r
is small. The method of moments, convenient in practice, is applied only for the first approximation, and the resulting estimates are less effective than the maximal likelihood estimates. In addition, both methods mentioned above require certain assumptions on the distribution of the parameters being studied, which is impossible to apply to interior characteristics. The method with weighted observations relies on decreasing or increasing the volume of the sample, which can negatively affect the information contained in it. The least squares method, under quite general assumptions on the nature of random errors and the structure of the distribution function, enables us to obtain consistent, asymptotically unbiased, asymptotically normal, and asymptotically effective estimates. Thus, taking into account the specific features of the methods under consideration, we prefer the least squares method.
It is necessary to write down an equation whose left-hand side contains the available values of interior characteristics (the matrix
B
) and the required matrix
F,
multiplying by which we obtain the matrix in the right-hand side containing the values of exterior characteristics (the matrix
V);
that is,
BF
=
V.
(2)
The sizes of known matrices are:
B
is a 7
x n
matrix;
V
is a 1
x k
matrix.
Consequently,
F
cannot be the required matrix, because its size cannot be chosen so as to allow the matrix multiplication in the left-hand side. Thus, (2) must have a different form, for instance,
LBP = V T,(3) AA+ A = A.(5) By (5), we rearrange (4) as L = V Tp + B+,(6) £ (lSit - lSrT)) ^ min i, (s,t)
In order to solve (7), find the extremum of the function in the left-hand side. Requiring that its derivative with respect to the unknown
i
S
rt
+1)
vanish, we obtain
(E^
s it
- i
s
T’)2)
'
=
2
E
(7
it
- i
S
d1’)
(
-
-) = о
,
i,
(
s,t
)
E (
i
SГ
- i
Sit
) = о
,
i,
(
S,t
)
whence
E
i
S
r
+1)
=
E
i
S
i
)
•
s,t s,t
i,
S
S,t
)
r ■ I
S
r
+
1
)
r·
s,t
i,
S
S,t
)
=
E
i
S
it
■
i,
S
S,t
)
Finally,
(
r
+i)
i
S,t
=
-
E
i
Sit
. r
,
i,
S
S,t
)
Thus, we may conclude that the entries of
L
'r
+1
) satisfying (7) amount to the mean values of the corresponding entries of the tuple
L
'ii.
Accordingly, the values of exterior characteristics for (
r
+ 1) variants of the IAS are determined in terms of the values of interior characteristics as
V
r
+
1
=
(
l
S
r
+1)
в
t
r
+1)
p
)
T
,
while the required values of interior characteristics, in terms of the specified values of exterior characteristics as
B
r
+1
=
1)
)
+
V
T
P
+
,
Example
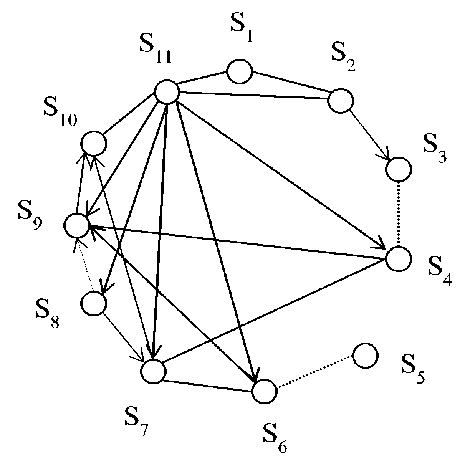
1. Consider an application of the proposed method for developing variants of IAS on a concrete example. A mathematical model of the IAS of an interior affairs department is represented [2] by a marked and weighted digraph
G
W
(see Figure).
Dotted lines show conflict relations, and solid lines show cooperative relations. Mutual relations in which
S
i
influences
S
j
a nd
S
j
also in fluences
S
i
are shown without arrows (edges of the digraph), and nonmutual relations in which
S
i
influences
S
j
are shown with arrows indicating the action (arcs of the digraph).
For
G
W
we calculated the values of interior characteristics (see Tab. 1). Tab. 2 shows the values of exterior characteristics.
The digraph G
w.
S1 is the server part, S2 is the block for processing the data of exterior
sources. S
3
is data, storage. S4 is the block of inquiries. S5 is the base of models. 8б is the block
controlling model experiments, S7 is the analysis block, S8 is the block of reference information, S9 is the plotting device, S1o is the decision maker, S11 is the block controlling the processes
Table 1 The values of interior characteristics
The vertices
s
1
s
2
s
3
s
4
s
5
s
6
s
7
s
8
s
9
s
10
s
11
M
+
0,57
0,4
0,14
0,63
1
0,83
0,75
0,6
0,68
0,67
0,71
D
k
2
2
2
2
2
2
2
4
2
2
2
S
k
9
9
9
9
2
9
9
6
9
9
9
V
min
0,077
0,077
0,077
0,022
0,3
0,072
0,022
0,022
0,022
0,022
0,022
V
max
1
1
0,32
0,8
0,3
1
1
0,3
0,8
1
1
B
k
3
3
12
2
5
3
2
7
3
2
2
M
k
23
23
23
23
5
23
23
22
23
23
23
Table 2 The values of exterior characteristics
Responsiveness, hours
Crime detection rate, %
Crime level, %
V(1)
1
15
60
Define the matrix
P
as
0
,
5
-
0
,
1
0
,
6
0
,
2
0
,
7
-
0
,
3
1
-
2
3
P
: =
5
5
5
-
3
2
1
0
,
1
0
,
2
0
,
3
0
,
8
0
,
5
0
,
2
Then in accordance with (6) we obtain
L
(1) = (0
,
73
,
0
,
29
, -
0
,
25
,
1
,
21
,
0
,
02
,
1
,
12
, -
1
,
05
, -
0
,
02
,
0
,
38
, -
1
,
26
, -
1
,
15)
Suppose that in the model G
w
we introduce an atIditional arc from 511 to s5 defining a cooperative relation. Tab. 3 presents the results of calculating interior characteristics and Tab. 4 shows the new values of exterior characteristics.
The values of interior characteristics The values of exterior characteristics Table 3
The vertices
s
1
S
2
S
3
S
4
s
5
s
6
s
7
s
8
s
9
s
10
s
11
M
+
0,57
0,4
0,14
0,57
0,2
0,62
0,65
0,6
0,59
0,57
0,62
D
k
2
2
2
2
2
2
2
4
2
2
2
S
k
9
9
9
7
9
9
9
6
9
9
9
V
min
0,077
0,077
0,077
0,022
0,072
0,072
0,022
0,022
0,022
0,022
0,022
^
imax
1
1
0,32
0,8
1
1
1
0,3
0,8
1
1
B
k
3
3
12
2
5
3
2
7
3
2
2
M
k
23
23
23
23
21
23
23
22
23
23
23
Table 4
Responsiveness, hours
Crime detection rate, %
Crime level, %
V
(2)
0,9
16
60
Then in accordance with (6) we obtain
L
(2) = (0
,
86
,
1
,
50
, -
0
,
11
, -
0
,
47
, -
0
,
89
,
0
,
42
, -
0
,
87
,
0
,
07
,
0
,
75
, -
0
,
57
, -
0
,
76)
Consider another variant of a structure-parametric change of the system. Suppose that, upon analyzing the results of the work of IAS, we managed, by restructuring it, to remove the conflict action
S
8
and
S
9, which corresponds to deleting the arc between
s
8 and
s
9. Tab. 5 shows the new values of interior characteristics.
Table 5
vertices
s
1
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
9
S
10
S
11
M
+
0,57
0,4
0,14
0,57
0,2
0,62
0,65
0,6
0,59
0,57
0,62
D
k
2
2
2
2
2
2
2
4
2
2
2
S
k
9
9
9
7
9
9
9
6
9
9
9
V
min
0,077
0,077
0,077
0,022
0,072
0,072
0,022
0,022
0,022
0,022
0,022
V
mmax
1
1
0,32
0,8
1
1
1
0,3
0,8
1
1
B
k
3
3
12
2
5
3
2
7
3
2
2
M
k
23
23
23
23
21
23
23
22
23
23
23
The values of exterior characteristics Table 6
Responsiveness, hours
Crime detection rate, %
Crime level, %
V
(3)
0,7
17
55
The values of interior characteristics Then in accordance with (6) we obtain
L
(3) = (1
,
05
, -
0
,
07
, -
0
,
35
,
0
,
76
, -
0
,
24
,
2
,
36
, -
1
,
24
,
0
,
13
,
0
,
46
, -
1
,
63
, -
1
,
37)
Basing on the resulting values of
L
(1)
, L
(2)
, L
(3), we find the matrix
L
necessary for solving problems 1 and 2 as
L
= (0
,
88
,
0
,
57
, -
0
,
24
,
0
,
5
, -
0
,
37
,
1
,
3
, -
1
,
05
,
0
,
06
,
0
,
67
, -
1
,
15
, -
1
,
09)
.
Then in the case of changing the model
G
W
we can predict the values of exterior characteristics of the IAS. For instance, remove the influence of the block of inquiries
s
4
on the analysis block
s
7; then the values of interior characteristics (see Tab. 7) enable us to find the exterior characteristics (see Tab. 8).
We conclude that this change of the system worsens the exterior characteristics, and consequently, reject removing the influence of s4 on s7. Similarly we can predict exterior estimates for other structure-parametric changes of the information-analytical system. Conclusion Relating the interior balance estimates for the system and its exterior characteristics, (9) and (10) both guarantee the developer the prediction of the general state of conflict of the interaction among interior elements to meet the specified effectiveness and determine how applicable the IAS is for solving the intended official tasks given the syntesized structure-parametric connections. In addition, it is possible to design the structure and determine the parameters of interaction among the elements of the IAS of an internal affairs department in the presence of external requirements concerning its effectiveness in official work. ш Table 7
The vertices
s
1
s
2
s
3
s
4
s
5
s
6
s
7
s
8
s
9
s
10
s
11
M
+
0,8
0,67
0,33
0,75
1
0,75
0,75
0,8
0,84
D
k
2
2
2
2
2
2
2
4
2
2
2
S
k
7
7
7
7
2
6
6
6
7
7
7
V
min
M 0,096
M 0,096
M
0,096
0
0
0
0
M 0,048
M
0,096
M
0,096
M
0,096
V
max
1
1
0,2
0,3
0,3
1
1
0,3
0,8
1
1
B
k
3
3
12
9
5
3
3
7
3
2
2
M
k
22
22
22
22
5
13
14
14
22
22
22
The values of exterior characteristics Table 8
Responsiveness, hours
Crime detection rate, %
Crime level, %
V
(3)
0,7
17
55
The values of interior characteristics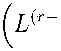
Список литературы Structural parametric modelling of an information-analytical system
- Пьянков, О.В. Информационно-аналитическая система: назначение, роль, свойства/О.В. Пьянков//Информационная безопасность регионов. -2014. -Т. 1, № 14. -С. 21-26.
- Пьянков, О.В. Математическое моделирование информационно-аналитической системы на основе теории конфликтов/О.В. Пьянков//Вестник Воронежского государственного технического университета. -2014. -Т. 10, № 1. -С. 75-79.
- Пьянков, О.В. Комплексная оценка сложной системы на основе теории конфликтов/О.В. Пьянков//Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. -2014. -№ 1. -С. 34-39.
- Меньших, В.В. Структурная адаптация систем управления/В.В. Меньших, В.В. Сысоев. -М.: Радиотехника, 2002.
- Men'shikh, V.V. Conflict Interactions in the Course of Synthesis of the Parameters of Control Actions in Multiple-Objective Control Systems/V.V. Men'shikh, V.V. Sysoev//Automatic Control and Computer Sciences. -2002. -V. 36, № 6. -P. 29-32.
- Айвазян, С.А. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное изд./С.А. Айвазян, И.С. Енюков, Л.Д. Мешалкин. -М.: Финансы и статистика, 1983.
- Гантмахер, Ф.Р. Теория матриц/Ф.Р. Гантмахер. -М.: ФИЗМАТЛИТ, 2004.


