Структура одномерных стоячих МГД-волн в дневной плазмосфере и на ее границе

Основные принципы, на которых основан предлагаемый здесь метод обработки записей колебательных процессов, были сформулированы в работе [Поляков, Потапов, 2001]. Под обработкой в данном случае подразумевается определенная последовательность программно реализованных численных процедур, которые служат для преобразования исходной записи сигнала. Примером может служить любой метод цифровой фильтрации или метод спектрального анализа, когда исходный сигнал преобразуется в зависимость спектральной функции от частоты. В предлагаемом методе конечным продуктом преобразования являются корреляционные функции флуктуаций амплитуды и фазы (КФАФ) обрабатываемого сигнала. В работах [Поляков, 2010 а , б ] этот метод был весьма успешно использован для исследования структуры стоячих сейсмических волн в оболочках Земли.

Рассмотрим участок почти монохроматических колебаний, которые содержат малые по величине случайные изменения амплитуды и фазы. В этом случае спектральная линия участка имеет небольшой разброс по частоте, а на записи каждое отдельное колебание по своей форме, амплитуде и периоду немного отличается от всех остальных. Среди колебаний естественного происхождения так выглядят, например, регулярные геомагнитные пульсации Pc1 и Pg, которые могут иногда сохранять этот колебательный режим в течение нескольких часов. Согласно работе [Гудзенко, 1961], подобные колебания можно считать периодически нестационарным случайным процессом, для которого справедливо обобщение эргодической теоремы. Это означает, что по всем отдельным колебаниям, которые входят в состав участка записи, мы можем определить одно среднее колебание, которое периодически повторяется от начала до конца участка. Кроме того, при определении авто- и кросскорреляционных функций случайных изменений амплитуды и фазы мы можем использовать усреднение по ансамблю реализаций отдельных колебаний на участке записи. Именно в таком способе определения корреляционных функций заключается главная особенность предлагаемого здесь метода обработки, которая отличает его от всех прочих методов. Другой особенностью является использование алгоритма практического определения среднего колебания, предложенного в работе [Гудзенко, 1962]. Этот алгоритм был положен в основу компьютерной программы, созданной при выполнении исследований в работах [Поляков, Потапов, 2001; Polyakov, Potapov, 2003]. Порядок выполнения процедур обработки и их основные алгоритмы подробно описаны в указанных работах. Поэтому здесь просто кратко перечислены основные этапы обработки.

Исходным является временной ряд цифровых отсчетов x ( t_i ), соответствующий интервалу записи колебательного процесса. После предварительной обработки (устранение выбросов, фильтрация и т. д.) каждое значение x ( t_i ) и время t_i нормируется соответственно средней амплитудой и средним периодом колебаний в интервале. Для каждого отсчета определяется производная y ( t i )= dx / dt , и точки x ( t i ), y ( t i ) наносятся на фазовую плоскость прямоугольных координат ( x , y ). Каждое отдельное колебание на этой плоскости образует замкнутую траекторию (цикл), при малых флуктуациях не слишком отличающуюся от окружности единичного радиуса. Среднее колебание или средний цикл определяется методом последовательных приближений, алгоритм которого подробно описан в [Гудзенко, 1962]. После этой процедуры для всех точек x ( t i ), y ( t i ) исходных циклов определяется фаза среднего колебания Θ i и отклонение вдоль направления нормали от среднего цикла n (Θ i ). Тангенциальные отклонения точек определяются соотношением γ(Θ i )=Θ i –t i . Физически фаза среднего колебания

О = tot = 2п t, где to = 2п - средняя частота с учетом нормировки времени. Нормальные и тангенциальные отклонения n и y соответствуют случайным флуктуациям амплитуды и фазы колебаний. Полученные таким образом значения зависимостей n(0i), y(0i) и их производных по времени dn /dt(0 i), dу/dt(0 i) позволяют определить для них кросс- и автокорреляционные функции. Конечным продуктом перечисленных процедур обработки являются не сами эти функции, а их алгебраические комбинации, определяемые по формулам

G ( О , т ) = (у ( О ) у ( О - т)) ( n ( О ) n ( О - т )) -

• - (у ( О ) n ( О - т )) ^ n ( О ) y ( О - т )),

G 1 ^{( О} , ^{т )} = 0 ' ^{( О )} У ^{( О - т )}) (у ^{( О )} n ^{( О - т}Н^-

• - ( n ( О ) n ( О - т )) (у ( О ) у ( О - т )),

G ₂ ( О , т ) = - (у ( О ) у ( О - т)} (у ( О ) n ( О - т )) +

+ (у (О) n (О - т)} (у (О)у (О - т)), где точка над символом означает производную по фазе 0, угловые скобки - усреднение по ансамблю отдельных колебаний, т - сдвиг фазы. Зависимость этих функций от фазы 0 по определению является периодической, поэтому ее можно представить в виде ряда Фурье, коэффициенты которого зависят только от т. Конечным продуктом обработки являются коэффициенты нулевой гармоники ряда Фурье, которые совпадают со средними по фазе значениями каждой из функций. Эти зависящие от τ средние для простоты, не меняя особо смысла, будем называть корреляционными функциями флуктуаций амплитуды и фазы (КФАФ).

По результатам работ [Поляков, Потапов, 2001; Поляков, 2010а, б] оказалось, что эти функции обладают очень любопытным и полезным для их дальнейшего использования свойством. Для колебаний в любой из точек внутри резонатора или волновода зависимости КФАФ от т имеют вид последовательности максимумов (пиков), следующих друг за другом через равные интервалы.

В работе [Поляков, Потапов 2001] рассмотрена модель простейшего одномерного резонатора с «закрепленными» концами, колебания в котором возбуждаются волной «вынуждающей силы». Для колебаний в точке, находящейся вблизи одного из концов, удалось получить аналитические соотношения для КФАФ в приближении, когда частота источника не сильно отличается от одной из собственных частот резонатора. Оказалось, что зависимость КФАФ от т определяется рядами гармонических функций (синус или косинус кратного аргумента), х = (to( / to)т, где to, О| - частоты источника и первой гармоники резонатора. Суммирование производится по номерам гармоник. Результатом суммирования являются чередующиеся через равные интервалы пики, а положение пика на оси т определяется условием для аргумента x=2п к:

т_к = 2 п к —,                                (2)

ω где к - номер пика. Интервал между двумя соседними пиками

ω

^А = ^т к + 1 ^-т к = ^{2 п}— •                         <31

ω

Перечисленные свойства КФАФ напоминают принцип действия дифракционной решетки. Действительно, угловое распределение интенсивности света после прохождения через дифракционную решетку также определяется рядами гармонических функций кратного аргумента. Отличие состоит только в том, что суммирование производится по номерам не гармоник, а щелей решетки. Из условия, накладываемого на аргумент этих функций, следует известное условие для углового положения пика интенсивности, совершенно аналогичное условию (2). Получается, что пики зависимостей КФАФ от т являются аналогом спектральных линий дифракционной решетки.

Обнаруженное сходство вызывает естественное желание попытаться использовать метод КФАФ так же, как используется дифракционная решетка, т. е. для измерений. На входе программы обработки мы имеем запись колебаний в точке резонатора, а на выходе получаем последовательность пиков (линий) на зависимостях КФАФ от τ. По этим пикам можно напрямую измерить интервал А . Частота to совпадает со средней частотой на исходном участке записи колебаний. Соотношение (3) дает возможность косвенного измерения to 1 . Таким образом, если дифракционная решетка предназначена для определения длины волны света, то с помощью метода КФАФ мы можем экспериментально измерять частоту первой гармоники резонатора.

Результаты модельного численного эксперимента

Рассмотрим более реалистичную для геомагнитных пульсаций модель, основанную на уравнениях МГД для плоского слоя при однородной плотности плазмы и постоянного магнитного поля , направленного вдоль оси OZ:

+ 8^ = V 2    + V 2    , д t2      д t        дz2       дx2

д2bx + 5dbL = (  д2bx _ (  д2bz dt2      dt        дz2       дxдz ’ где bx, bz - компоненты возмущения магнитного поля, V- альфвеновская скорость, 5 - декремент затухания.

Резонатором будем считать прямоугольник со сторонами l_x , l_z вдоль осей OX и OZ соответственно. Граничные условия соответствуют «закрепленным» концам:

bx (0, z) = bx (lx, z) = bz (lx, z) = 0, bx (x, 0) = bx (x, lz) = bz (x, 0) = bz (x, lz) = 0.

Источником, возбуждающим волны в резонаторе, будем считать колебания b_z- компоненты на стороне, расположенной на оси OZ:

b_z (0, z ) = f ( z , t ) = sin( kz ) [ sin( to t ) + F ( t ) ] (5) при

0 < z < 1г, где ω и k – частота и волновое число колебаний в источнике, F(t) – функция, определяемая случайным временным процессом. Наличие случайной функции в источнике необходимо по той причине, что без нее временные флуктуации амплитуды и фазы колебаний в любых точках резонатора равны нулю. Для простоты в качестве F(t) нами был выбран обычный белый шум с гауссовским распределением, который при решении уравнений задавался генератором случайных чисел.

Соотношения (4), (5) представляют собой самые простые волновые уравнения из физики плазмы, дополненные простейшими граничными условиями. Поэтому их решения нельзя считать электродинамическими, т. е. они не могут описывать никакой реальный физический объект. В данной работе (4), (5) играют роль модели обычного, в определенном смысле произвольного, резонатора для МГД-волн. Мы моделируем сигналы при значениях параметров, которыми можно управлять. Конечной целью является обработка этих сигналов методом КФАФ для выявления закономерностей, связанных с пиками корреляционных функций.

Для численного решения была использована явная разностная схема ([Аки, Ричардс, 1983] метод конечных разностей) и соответствующая этой схеме последовательность алгоритмов вычислений. Задавая шаг пространственно-временной сетки h и значения параметров l_x , l_z , V , δ, ω, k , мы в результате вычислений получаем временные зависимости для компонент возмущения магнитного поля b_x ( t ) и b_z ( t ) в любой точке резонатора.

На рис. 1 приведен пример зависимостей от τ всех функций (1) для b x -компоненты в точке, расположенной вблизи одного из закрепленных концов резонатора. Видно, что, как и в случае с одномерным резонатором, эти зависимости представляют собой периодическую последовательность пиков или разрывов (для функции G ₁). При этом интервал между двумя соседними пиками

A = 2п^ = 2п —, (6) п V to, z где ω1z – частота первой гармоники альфвеновской стоячей волны.

Эта и остальные подобные формулы для интервала A получены в данной работе эмпирически. Вначале численно получаем решение b_x ( t ) в заданной точке. Затем для этого сигнала методом КФАФ получаем зависимости функций (1) от τ. Изменяя поочередно значения параметров модели и источника, отслеживаем связанные с ними изменения интервала между пиками A и определяем правую часть в соотношении (6).

Колебания b z -компоненты возмущения магнитного поля в модели плоского слоя обусловлены стоячими БМЗ-волнами. Для них эмпирическая формула для интервала между пиками A имеет вид

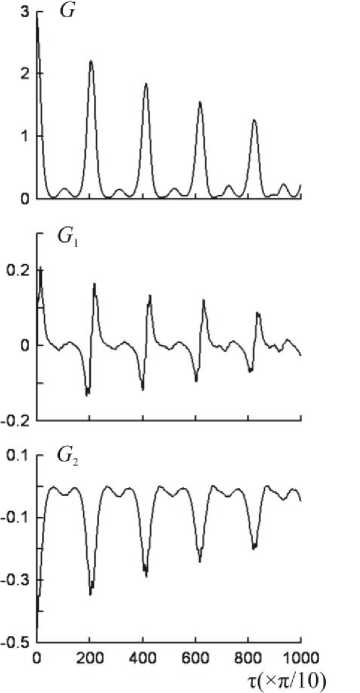
Рис. 1 . Пример зависимости всех КФАФ от фазового сдвига τ для колебаний b_x -компоненты возмущения магнитного поля в модели плоского слоя.

A = 2п^ = 2п —, (7) п V to1 x где ω1x – частота первой гармоники одномерной стоячей волны вдоль оси OX. Если источник – функцию f(z, t) в (5) – перенести на смежную сторону резонатора, расположенную вдоль оси OX, заменив при этом z на x, то аналогичная эмпирическая формула будет иметь вид

A = 2п—z- = 2п—, (8) п V to, z где ω1z – частота первой гармоники одномерной стоячей волны вдоль оси OZ. Получается, что для таких изотропных волн в двумерном резонаторе интервал между соседними пиками КФАФ может определяться только двумя частотами, каждая из которых соответствует стоячей волне вдоль одной из координатных осей.

Рассмотрим ситуацию, когда резонатор вдоль координаты x разделен на две области с разными значениями альфвеновской скорости V 1 и V 2 (рис. 2, б ). В пределах каждой области скорости одинаковы во всех точках. Координату границы между областями обозначим l_{x 1}. Положение источника задается соотношением (5). Это означает, что интервал между пиками A должен определяться частотой ю 1 _х одномерной стоячей волны вдоль координаты x . На рис. 2, а приведены зависимости G (τ) при различных соотношениях между скоростями V ₁ и V ₂ для колебаний

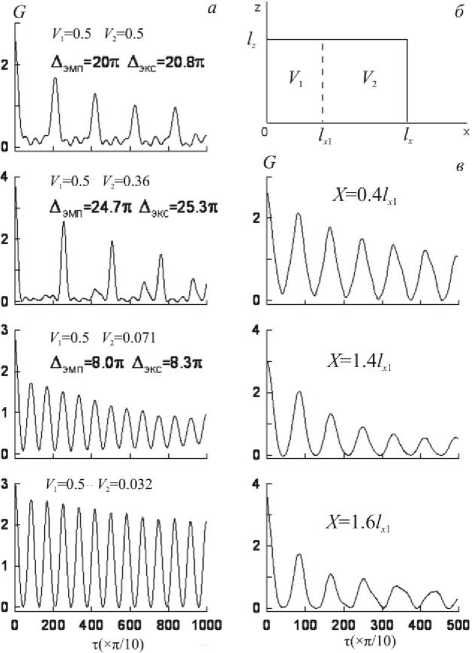
Рис. 2 . Зависимость КФАФ от τ в случае неоднородной модели стоячих БМЗ-волн: функция G (т) при различных значениях альфвеновской скорости первой и второй области ( а ); схема модели резонатора ( б ); функция G (т) для колебаний в точках с разными координатами ( в ).

b z -компоненты в точке, расположенной внутри первой области. Для верхней панели скорости обеих областей одинаковы. Такая ситуация полностью соответствует рассмотренному выше случаю однородного резонатора. Поэтому интервал А _экс, экспериментально измеренный по положению пиков на графике, практически точно совпадает с интервалом А _эмп, вычисленным по эмпирической формуле (7) с подстановкой всех заданных параметров модели. На следующей панели скорость V 2 в 1.4 раза меньше скорости V 1 . Интервал А _экс заметно увеличивается, при этом эмпирическая формула для него имеет вид

А = 2п— = 2 п T x , (9) ® 1 х T

Т — 7 I lx 1 I lx   lx 1 I

T 1      ^{2      +}            ,

1 x

V ^V 1        V 2    )

где Т - период колебаний bz-компоненты в точке наблюдения. Период первой гармоники T1 x равен времени пробега волны (туда и обратно) через обе области вдоль координаты x. Получается, что в данном случае частота первой гармоники ю1 x соответствует стоячей волне, запертой между внешними границами первой и второй областей резонатора. На следующей панели скорость V2 снова уменьшается относительно V1, но уже в 7 раз. При этом видно, что интервал Аэкс не увеличивается, а резко уменьшается. Более того, при еще большем уменьшении скорости V2 (самая нижняя панель) этот интервал вообще остается без изменения. Эмпирическое соотношение для этих двух случаев имеет вид (9) при условии

• 1.    = 2 ^{1x 1}.

^{1 x} V

Получается, что ю 1 _x в этом случае является частотой первой гармоники стоячей волны, запертой только в первой области. Очевидно, что переход в значениях А от одной стоячей волны к другой обусловлен увеличением коэффициента отражения на границе между областями. Это свойство КФАФ позволяет сделать важный вывод. Если в реальном магнитосферном резонаторе вдоль одной из координат число точек отражения больше двух, интервал А будет определяться частотой первой гармоники таких стоячих волн, которые запираются между двумя точками поворота при всех возможных комбинациях этих пар.

На рис. 2, в приведены зависимости G (т) для случая со значениями скоростей V 1 =0.5 и V 2 =0.071, когда интервал А определяется стоячей волной только в первой области. Они отличаются друг от друга тем, что получены для колебаний в точках с разными координатами x . Верхняя панель соответствует точке, расположенной внутри первой области. Для двух других зависимостей точка наблюдения находится за пределами этой области. Отчетливо видно, что интервал А во всех случаях имеет одинаковое значение, несмотря на то, что на нижней панели пики заметно искажены. Получается, что по значениям интервала А можно обнаружить одномерную стоячую волну даже в том случае, если точка наблюдения колебаний находится на существенном расстоянии от одной из границ за пределами той области, где локализована эта волна.

В магнитосфере вследствие немонотонного распределения скорости вдоль радиальной координаты альфвеновские волны могут быть заперты не только вдоль, но и поперек магнитного поля. При этом область существования таких стоячих волн можно считать двумерным резонатором альфвеновских волн. В работе [Гульельми, Поляков, 1983] было показано, что учет малой поперечной дисперсии дает возможность определения положения таких резонаторов вдоль радиальной координаты. В работе [Леонович, Мазур, 1987] один из них был обнаружен на внешней кромке плазмопаузы в окрестности максимума альфвеновской скорости.

С учетом поперечной дисперсии дисперсионное уравнение альфвеновских волн имеет вид ю2 = kz V 2(1 + S2 kx2). (10)

Масштаб поперечной дисперсии S в области с холодной плазмой внутри плазмосферы определяется электронной инерционной (скиновой) длиной, а в области с горячей плазмой кольцевого тока - ларморовским радиусом протонов.

Этому уравнению соответствует уравнение в частных производных для bx-компоненты возмущения магнитного поля. Так же как для модели плоского слоя, резонатор будем считать прямоугольным с размерами lx, lz с аналогичными граничными усло- виями. Для колебаний в таком резонаторе альфве-новских волн полученная эмпирическим путем формула для интервала между соседними пиками КФАФ имеет вид

ωll       ωA = 2п--= 2п , п VSm     rojx

где m – номер гармоники стоячей волны вдоль направления магнитного поля. В отличие от всех прочих рассмотренных типов волн правая часть в (11) определяется более сложной комбинацией параметров и зависит от целого числа m , которое может принимать бесконечное число разных значений.

Собственная частота прямоугольного однородного резонатора альфвеновских волн получается, если в (10) заменить k x и k z на собственные значения π/ l x и π/ l z :

п2m2 2п п2 m2 п2n2 ro- = V — + V S — z zx

Второе слагаемое в правой части определяет частоту стоячей волны поперек направления магнитного поля. Частота первой гармоники этой волны по поперечному номеру n

ro = VSm--.

• ¹    ^ l x l z

Интересно, что, хотя соотношение (11) получено эмпирически, в знаменателе правой части по комбинации параметров оказалась точно такая же частота.

Во всех без исключения рассмотренных выше случаях эмпирическое соотношение для интервала между соседними пиками КФАФ имеет одинаковый, универсальный вид (3). При этом ω1 в знаменателе правой части является частотой первой гармоники одной из одномерных стоячих МГД-волн любого типа между двумя из всех возможных точек поворота внутри резонатора или волновода. Именно эту частоту можно измерять с помощью предлагаемого в данной работе метода обработки сигналов.

В заключение этого раздела рассмотрим влияние неоднородности скорости вдоль направления стоячей волны. Будем считать, что в модели плоского слоя (4), (5) зависимость альфвеновской скорости от координаты вдоль постоянного магнитного поля имеет вид

V ²( z ) = V ₀ ² +в ( z - l z /2)². (12)

При такой параболической зависимости минимальное значение скорости V 0 будет в центре магнитной линии, а максимальное V (0) – на ее краях.

В однородном случае для стоячей волны bx-компоненты получается соотношение (6). По этой формуле с учетом (12) эмпирически можно определить частоту ω1z, или, вернее, то, что находится в знаменателе правой части. На рис. 3 крестиками отмечена эта частота при различных отношениях скоростей V(0) и V0. Здесь же приведены собственные частоты первой и второй гармоник для стоячей волны вдоль координаты z. Для нормировки использована частота ω1 первой гармоники при V(0)=V0. Отчетливо видно, что крестики совпадают с тре- угольниками, а не с кружками. Это означает, что эмпирическая формула для интервала Δ при неоднородной скорости (12) должна иметь вид

A = 2 п

ω ro2z /2

где ω 2 z – частота второй гармоники.

Полученное соотношение позволяет сделать важное обобщение формулы для интервала Δ . Оказывается, что при параболической зависимости скорости (12) все собственные частоты становятся эквидистантными, начиная со второго номера гармоники. При этом значение ω_{2 z} /2 совпадает с разностью частоты двух соседних гармоник. В случаях с однородной скоростью собственные частоты эквидистантны с первого номера и частота первой гармоники в знаменателе правой части (6), (7), (8), (9) и (11) также совпадает с разностью частот двух соседних гармоник. Очевидно, что в общем случае при произвольной зависимости волновой скорости от координаты вдоль направления стоячей волны соотношение для интервала между пиками должно иметь вид

A = 2 п

ω

ГО + 1 ^-ro ,

где i – номер гармоники, начиная с которого собственные частоты стоячей волны ω _i становятся эквидистантными или почти эквидистантными.

Использование метода КФАФ для обработки записей геомагнитных пульсаций

В этом разделе попытаемся применить метод КФАФ для обработки реальных, а не моделированных записей геомагнитных пульсаций. Для анализа были выбраны записи северо-южной компоненты возмущения геомагнитного поля на станциях Борок (L=2.9) и Монды (L=2.2) в течение одного часа от 9 ^h до 10 ^h UT 10.04.00. Шаг оцифровки обеих записей составляет 0.1 с. Поле магнитосферы в это время характеризуется средним уровнем возмущенности с индексом K _p=3. Обе точки наблюдения возмущений

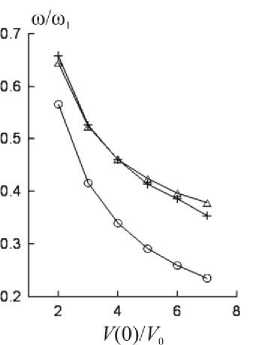
Рис. 3 . Влияние продольной неоднородности скорости на значение интервала между соседними пиками КФАФ. Кружки о - частота первой гармоники; треугольники A -частота второй гармоники, деленная на 2; крестики + – частота, измеряемая методом КФАФ.

при этом находятся на освещенной стороне внутри плазмосферы.

Первый этап обработки заключается в узкополосной фильтрации исходного сигнала. Для этого использовался немного модифицированный для наших целей фильтр Марме [Marmet, 1979]. Всего было использовано 20 различных фильтров, которые отличаются друг от друга значением центральной частоты полосы пропускания. Период колебаний с этой частотой лежит в диапазоне 0.6–5.4 с.

После фильтрации вся часовая запись разбивается на отдельные участки, вмещающие 30–40 отдельных колебаний. Для каждого такого участка записи почти монохроматических колебаний компьютерная программа метода КФАФ выдает зависимости корреляционных функций G , G 1 и G 2 от сдвига фазы τ.

Первые же опыты обработки по указанной схеме позволили обнаружить любопытную особенность. Оказалось, что для некоторых участков указанные корреляционные функции по характеру зависимости от τ сильно похожи на те, которые получаются для колебаний в модели плоского слоя. На рис. 4, а , б приведены примеры таких зависимостей для двух случаев. В каждом из них указано название станции, время начала участка колебаний, отчитываемое от начала часовой записи и средний период колебаний. Все три функции безразмерны, а сдвиг фазы τ с учетом масштабного коэффициента измеряется в радианах. На рис. 4, в для сравнения приведены те же функции, полученные для альфвеновских колебаний в модели плоского слоя из предыдущего раздела данной работы. Сравнение графиков обнаруживает их абсолютное подобие. Действительно, функция G (τ) на рис. 4, а , б так же как и на рис. 4, в , имеет вид периодической последовательности пиков. При этом в обоих случаях между главными пиками наблюдаются небольшие по высоте дополнительные пики. Функции G 1 (τ) для реальных колебаний, так же как и для моделированных, имеют вид последовательностей разрывов, или резких скачков от отрицательных значений к положительным. Функция G ₂(τ) на всех без исключения графиках имеет вид последовательности пиков, перевернутых вниз. Для реальных колебаний это особенно хорошо заметно на рис. 4, а .

Очевидно, что такое четкое подобие функций невозможно объяснить простым случайным совпадением, поскольку для каждого участка реальных колебаний не одна, а сразу три функции оказываются подобны теоретическим. Для данного исследования это подобие следует считать важным экспериментальным результатом, поскольку оно указывает на то, что интервал между соседними пиками Δ для геомагнитных пульсаций, так же как и для моделированных колебаний, должен определяться соотношением (3). Из него получается более удобная формула для периода первой гармоники одномерных стоячих волн

T = ^Δ T .

2π

Интервал между соседними пиками Δ удобнее всего измерить по графику G(τ) (рис. 4, а, б), период T колебаний после фильтрации совпадает с периодом колебаний с центральной частотой полосы пропускания, следовательно, по этой формуле мы можем косвенно измерить период T1.

Следует отметить, что для реальных стоячих волн в системе ионосфера–магнитосфера скорость Альфвена может быть сильно неоднородна. При этом, согласно (13), период T ₁ должен соответствовать разности двух соседних собственных частот. В данной работе этот период мы будем считать периодом первой гармоники только лишь для того, чтобы он имел простой физический смысл.

Вся дальнейшая обработка записей возмущения магнитного поля была направлена на измерения периодов T 1 по указанной схеме. В результате по записи ст. Борок было получено примерно 1500 измерений, а по записи ст. Монды – 1600. Этого оказалось вполне достаточно, для того чтобы построить функции распределения значений T ₁ для каждой станции. Графики этих функций представлены на рис. 5. По оси ординат отложено число измерений N , которое приходится на то или иное значение T ₁, период (ось абсцисс) измеряется в секундах. Из сравнения рис. 5, а и б следует прежде всего, что в обоих случаях наблюдается одинаковая последовательность максимумов (пиков). Каждому такому пику на распределениях присвоен соответствующий номер.

При интерпретации полученных результатов необходимо иметь в виду, что, согласно выводам предыдущего раздела, каждому максимуму распределения должна соответствовать своя одномерная стоячая волна в магнитосфере, причем она может быть как альфвеновской, так и БМЗ-волной. Станция наблюдения колебаний должна при этом находиться внутри или где-то поблизости от того места, где эта волна локализована. В данном случае речь идет о стоячих волнах в дневной плазмосфере. Попытаемся выяснить, каким именно стоячим волнам соответствует каждый из пиков полученных распределений. Очевидно, что как минимум один из них должен быть обусловлен альфвеновской стоячей волной вдоль направления магнитного поля. При этом на разных L-оболочках эти пики должны иметь разные значения периода T ₁, т. е. на рис. 5, а и б они должны быть сдвинуты друг относительно друга. Чтобы сдвиги были лучше видны, проведены вертикальные штриховые линии. Сдвинутыми оказываются сразу три пика с номерами 2, 3 и 4. Величина сдвига для всех пиков примерно одинакова и составляет 2.2 с.

Сдвиг для этих трех пиков означает, что каждый из них должен быть обусловлен именно продольной альфвеновской волной. Наличие этих пиков легко объяснить, если учесть немонотонность изменения альфвеновской скорости вдоль направления магнитного поля. При этом все пространство вдоль поля между проводящими слоями в сопряженных ионосферах можно условно разделить на три области. Две из них называются ионосферными альфвеновскими резонаторами (ИАР) [Поляков, Рапопорт, 1981] и располагаются на концах магнитной линии в промежутках между максимумом альфвеновской скорости на высоте 800 км и проводящим слоем ионосферы.

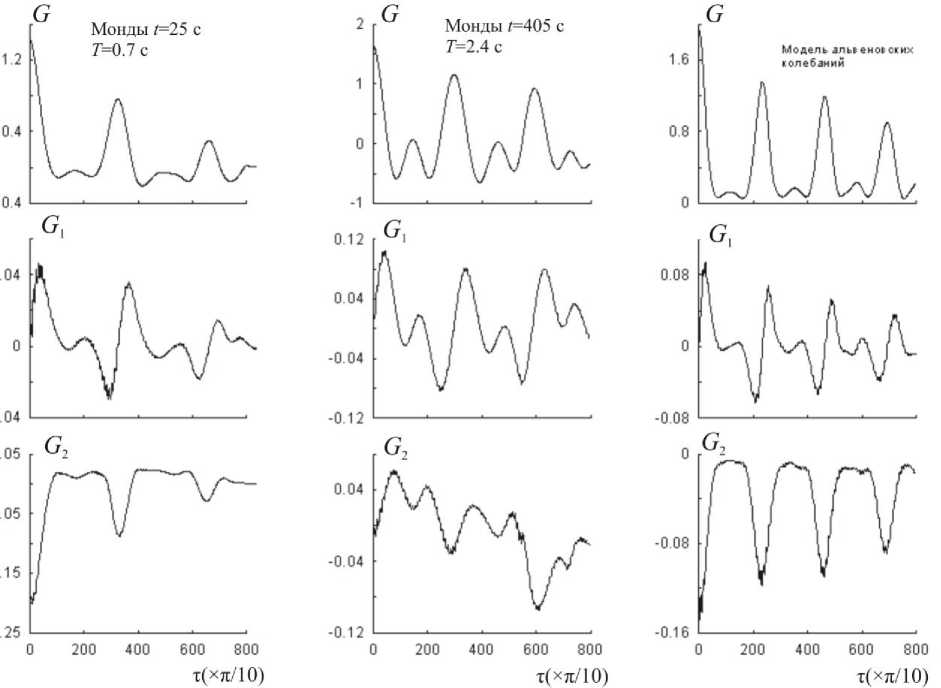
Рис. 4 . Примеры зависимостей КФАФ от τ для участков фильтрованных записей геомагнитных возмущений на станции Монды ( а , б); для альфвеновских колебаний в МГД-модели плоского слоя ( в ).

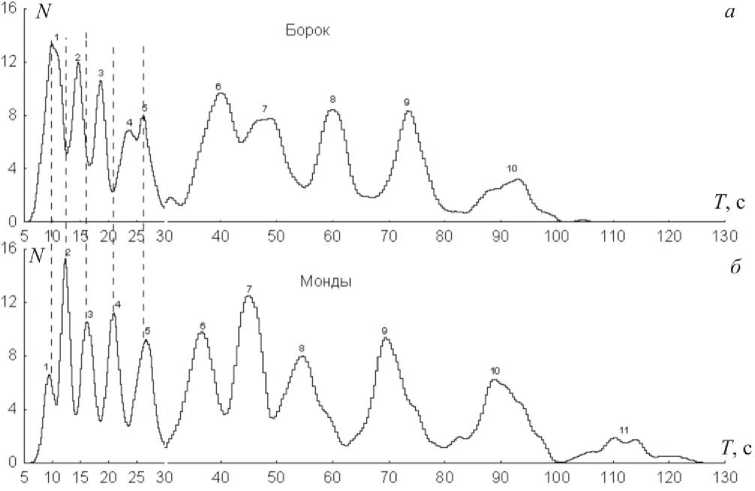
Рис. 5 . Функции распределения периода первой гармоники одномерной стоячей волны для станций Борок ( а ) и Монды ( б ).

Между максимумами скорости в сопряженных ионосферах расположена третья магнитосферная область. Граница между двумя областями является точкой поворота для продольных альфвеновских волн. В этом случае, как было показано в первой части, должно наблюдаться несколько характерных значений периода T1, каждое из которых соответ- ствует стоячей волне между двумя такими точками при всех возможных комбинациях этих пар. Очевидно, что пик 2 на обоих распределениях соответствует стоячей волне на магнитосферном участке. Значение T1 для него определяется временем пробега между внешними границами ИАР в сопряженных ионосферах. Пик 3 соответствует стоячей волне между проводящим слоем ионосферы и максимумом альфвеновской скорости в сопряженной ионосфере. Период T1 при этом определяется суммой времени пробега магнитосферного участка и времени пробега одного ИАР. Пик 4 соответствует стоячей волне между двумя проводящими слоями, и его период равен сумме времени пробега на магнитосферном участке и времени пробега двух ИАР.

Разность значений T ₁ для пиков 2, 3 и для пиков 3, 4 должна совпадать с периодом первой гармоники стоячей волны в ионосферном альфвеновском резонаторе. На рис. 5 эта разность примерно одинакова для обеих пар пиков и для обоих распределений и составляет 4.3 с. В работе [Поляков, Рапопорт, 1981] период первой гармоники собственных частот ИАР, полученный теоретически для характерных параметров ионосферы, имеет почти то же значение 5 с.

Для интерпретации пиков 1 и 5 важным обстоятельством является тот факт, что каждый не имеет сдвига на распределениях станций Борок и Монды, что отчетливо наблюдается по вертикальным штриховым линиям. Это должно означать, что пики 1 и 5 обусловлены не альфвеновскими, а стоячими БМЗ-волнами. Пространственная структура, в которой внутри плазмосферы могут возникать такие волны, впервые была обнаружена в работе [Гульельми, 1972] и получила название магнитозвукового канала под сводом плазмосферы. Как было показано в первой части данной работы, этот канал должен давать такие значения периода T ₁, которые соответствуют периоду первой гармоники каждой из одномерных стоячих волн. Согласно [Гульельми, 1972], период первой гармоники стоячей волны поперек магнитного поля в радиальном направлении соответствует нижнему пределу частотного диапазона канала и имеет значение 10 с. Это хорошо согласуется с периодом T 1 =10 c пика 1 для обоих распределений на рис. 5, значит, пик 1 обусловлен стоячей волной радиального направления. В работе [Гульельми, 1972] приведены изолинии распределения альфвеновской скорости дневной плазмосферы в меридиональной плоскости. Хорошо видно, что размер канала в радиальном направлении примерно в три раза меньше его размера вдоль направления магнитного поля. Если считать, что период T ₁ определяется временем пробега между точками поворота, то его значение для радиального направления также должно быть в три раза меньше, чем для направления вдоль магнитного поля. На рис. 2 для обоих распределений отношение периодов T 1 пика 5 и пика 1 составляет примерно 2,7, т. е. неплохо соответствует указанному соотношению. Это значит, что пик 5 соответствует одномерной стоячей волне вдоль направления магнитного поля.

Главным отличительным признаком остальных пиков являются большие значения периодов T ₁. Это требует слишком большого расстояния между точками поворота для обычных стоячих МГД-волн при тех значениях альфвеновской скорости, которые характерны для плазмосферы. Кроме того, пиков слишком много, чтобы можно было пытаться интерпретировать их обычными альфвеновскими и стоячими БМЗ-волнами.

Наиболее подходящим объяснением для пиков с номерами 6–11 является их связь с поперечной стоячей альфвеновской волной вдоль радиального направления. Как было уже упомянуто в первой части, такие стоячие волны могут быть локализованы на внешней кромке плазмопаузы в окрестности максимума альфвеновской скорости. Для таких стоячих волн для периодов T ₁, которые в данной работе измеряются методом КФАФ, имеет место соотношение

T=Δ T=lT1z , (14) 2π πSm где T1z – период первой гармоники вдоль магнитного поля или время пробега вдоль поля с альфвеновской скоростью (туда и обратно) между точками поворота, m – номер гармоники продольной стоячей волны, l – расстояние между точками поворота в поперечном радиальном направлении, S – масштаб поперечной дисперсии, который в данном случае совпадает с ларморовским радиусом протонов кольцевого тока. Эта формула позволяет без особых противоречий объяснить наличие пиков 6–11. Действительно, как было уже показано выше, период T1z может принимать три разных значения, значит для каждого номера m гармоники в соотношении (14) должны иметь место три пика, аналогичные пикам 2, 3 и 4 продольных стоячих альфвеновских волн на L-оболочках ст. Борок и ст. Монды. При этом интервал между соседними пиками в тройке должен быть одинаковым и определяться временем пробега волны в ионосферном альфвеновском резонаторе. Очевидно, что одной такой тройкой с m=2 являются пики с номерами 6, 7 и 8, поскольку интервалы между пиками 6, 7 и 7, 8 почти совпадают. Остальные пики с номерами 9, 10 и 11 образуют вторую тройку с m=1. Это подтверждается тем обстоятельством, что на обоих распределениях отношение периодов T1 для 9 и 6, для 10 и 7, и даже для 11 и 8 на рис. 5, б каждый раз оказывается равным 2.

Кроме того, соотношение (14) позволяет прояснить вопрос, связанный с большими значениями T 1 пиков с номерами 6–11. Очевидно, что эта особенность является прямым следствием наличия множителя l / s . Ларморовский радиус протонов кольцевого тока s должен быть равен нескольким десяткам километров. Поперечный размер резонатора l – это толщина плазмопаузы, которая составляет примерно 600 км, значит по порядку величины l / s ≈ 20. Для сравнения рассмотрим отношение периодов T ₁ пиков 2 и 9. Для пика 2 период T ₁ определяется временем пробега с альфвеновской скоростью магнитосферного участка на оболочке с L ≈ 2.5. Для пика 9 период T 1 z – это то же самое время, только для оболочки плазмопаузы. Для грубой оценки эти периоды можно считать одинаковыми. Из соотношения (14) с учетом того, что для пика 9 m =1, получаем l / s ≈ π T ₁₉/ T ₁₂. Для обоих графиков рис. 5 отношение периодов T 19 и T 12 девятого и второго пиков составляет примерно 7. В результате получается точно такая же оценка l / s ≈ 7π ≈ 20.

История изучения резонаторов и волноводов МГД-волн в плазмосфере насчитывает уже сорок лет. Об этом свидетельствует, например, дата выхода работы [Гульельми, 1972]. За это время существование перечисленных выше резонаторов и волноводов не один раз подтверждалось как теоретически, так и экспериментально. Поэтому для наших исследований плазмосферу можно считать своего рода эталонным объектом. Тот факт, что пики распределений на рис. 5 совершенно непротиворечиво интерпретируются известными стоячими волнами, должен убедительно подтверждать достоверность результатов, которые получаются с помощью метода КФАФ.

Заключение

Перечислим основные результаты.

• 1.    Для объемного резонатора изотропных волн в отличие от одномерного резонатора интервал Δ , определяемый методом КФАФ, определяется частотой первой гармоники каждой из одномерных стоячих волн в отдельности. Если вдоль одного из направлений имеют место не две, а несколько возможных точек поворота, то интервал Δ для этого направления определяется частотами каждой из стоячих волн при разных комбинациях двух таких точек.

• 2.    Для поперечных стоячих альфвеновских волн интервал Δ оказался зависимым от номера гармоники вдоль постоянного магнитного поля. Это значит, что он может принимать не одно, а бесконечное множество разных значений.

• 3.    Метод КФАФ впервые был использован для обработки реальных записей геомагнитных возмущений. Для записей станций Борок и Монды в качестве конечного продукта метода получены распределения периодов Т 1 .

• 4.    Оказалось, что все характерные значения этих периодов полностью соответствуют известным стоячим МГД-волнам в плазмосфере и на ее границе.