Структуризация и формализация как инструменты создания эффективной инновационной среды обучения взрослых

В настоящей работе мы предлагаем инновационный подход к созданию интеллектуальной среды для обучения и переобучения взрослых, названный нами эквивалентностно-группо-вым подходом. Он основан на использовании математической теории бинарных отношений [2] и теории и практики педагогических измерений [1]. Этот комплексный подход является оригинальным синтезом индивидуального и группового подходов в методологии андраго-гики, при этом опирается на современные технологии контекстного и компетентностного подходов [4, 5] к обучению взрослых.

Необходимость исследования процесса обучения и особенно переобучения взрослых обусловливается тем, что проблемы, связанные с этим процессом, хотя и являются далеко не новыми для человечества, приобрели в последние 20— 30 лет особую актуальность в мире, в том числе в России. Это, очевидно, объясняется тем, что в последние 50 лет резко ускорился процесс преобразований в мире во всех сферах жизнедеятельности человеческого общества. Большие массы населения, прежде всего взрослого, вовлеченные в эти процессы, меняют, чаще всего вынужденно, свой образ жизни, привычки, области деятельности.

Поэтому в некоторых странах, например, в Германии, США, Финляндии, раньше других осознавших масштабность и глубину этого процесса, стали уделять проблемам обучения взрослых повышенное внимание как в теоретическом, так и прикладном плане.

Этот процесс обучения взрослых (для отличия от обучения детей и подростков) еще в первой половине XIX века получил свое название — андрагогика. В мире существует достаточно обширная литература по вопросам андрагогики. Фундаментальной работой в этой области является книга американского специалиста М. Ноулза «Современная практика образования взрослых. Андрагогика против педагогики», изданная в 1970 году [3]. В ней изложены основные принципы обучения взрослых, сформулированные на основе анализа и обобщения имеющийся практики.

Этот труд не решает всех проблем андраго-гики. Так, с нашей точки зрения, актуальной проблемой андрагогики является проблема формализации некоторых положений современной теории андрагогики с целью развития известных или отыскания новых подходов к обучению и, особенно, переобучению взрослых.

Здесь под структуризацией какого-либо яв- ления или процесса мы понимаем выделение в этом явлении или процессе таких сторон, которые можно рассматривать как некоторые узнаваемые объекты, допускающие формальное описание. Формализация любого процесса или какой-либо теории на подходящем языке (в идеале, логико-математическая схематизация с использованием соответствующего математического аппарата) представляет собой более или менее «удачную» модель этого процесса (теории) или какой-то его (ее) отдельной стороны. Если модель действительно «удачна», то она позволяет раскрыть суть исследуемого процесса (теории) или его (ее) отдельных сторон. Это приводит к более осмысленному и четкому представлению о процессе (теории) и, одновременно, открывает пути для его (ее) более глубокого исследования. В частности, при удачном выборе способа формализации процесса выяснить причинно-следственные связи внутри этого процесса, оценить влияние тех или иных факторов (как внешних, так и внутренних) на ход процесса и, в конечном итоге, рассчитать его эффективность (в заданном смысле).

Поэтому, если для изучаемого нами процесса — процесса обучения взрослых, найти (сконструировать) некую формальную (лучше всего, математическую) модель, более или менее адекватную, в рамках достаточно разработанной теории, то это должно привести к новому знанию в существующей теории обучения. И, следовательно, оказаться полезным для развития общей теории обучения.

В данной работе и рассматривается такой подход к структуризации и формализации процесса обучения взрослых, основанный на математической теории бинарных отношений [2].

Остановимся сначала на более детальном рассмотрении процесса обучения взрослых и введем необходимые понятия. Будем изучать этот процесс (для большей конкретизации) как процесс профессионального переобучения «взрослого» специалиста, вызванного сменой требований к его компетенциям из-за изменения внешней среды. Предполагается, что процесс переобучения осуществляется в соответствующей интеллектуальной обучающей среде.

Любой процесс переобучения специалистов, естественно, начинается с ранжирования (классификации) специалистов по нескольким информативным признакам (параметрам). Как правило, эти параметры должны иметь интегральный характер для более или менее комплексной и объективной оценки каждого специалиста в индивидуальном порядке.

В настоящей статье мы рассмотрим классификацию специалистов на основе трех параметров:

• 1)    реальная степень компетентности специалиста в заданной области;

• 2)    уровень фундаментального и специального образования;

• 3)    способность к обучению и мотивация.

Нам представляется, что эти три признака в совокупности позволяют объективно оценить возможности специалиста к переобучению и адекватно определить программу его переобучения.

Задача классификации специалистов по каждому из указанных признаков формализуется как задача определения отношений на множестве переобучаемых специалистов. Для изучения отношений между объектами из некоторого абстрактного множества в математике применяется теория бинарных отношений.

Зададим множество всех специалистов, которые проходят профессиональное переобучение в заданной интеллектуальной среде, и обозначим его через S . В дальнейшем будем называть элементы (специалистов) данного множества объектами. Рассмотрим прямое произведение множества S на себя, то есть S * S . По определению прямого произведения множеств оно состоит из всех упорядоченных пар объектов ( s₁ , s 2 ), где объекты s₁ и s 2 принадлежат множеству S, то есть s 1 ϵ S и s 2 ϵ S .

Согласно теории бинарных отношений, любое подмножество из прямого произведения S * S является бинарным отношением между объектами множества S . Бинарное отношение (то есть подмножество) на множестве S * S можно задать либо простым перечислением его элементов, либо явным указанием некоторого свойства, связывающего объекты s₁ и s₂ из S .

Воспользуемся вторым способом задания бинарного отношения. В качестве такого свойства возьмем сначала первый параметр классификации специалистов, указанный выше, а именно степень профессиональной компетентности специалиста в начальный момент переобучения. Зададим бинарное отношение таким образом: упорядоченная пара объектов (– специалистов) ( s 1 , s 2 ) принадлежит бинарному отношению, если объекты s 1 и s 2 обладают «одинаковой» компетентностью в начальный момент переобучения.

Обозначим это бинарное отношение через K . Покажем, что определенное нами бинарное отношение K на прямом произведении S * S обладает свойствами рефлексивности, симметричности и транзитивности.

В самом деле, бинарное отношение K рефлексивно, так как для любого объекта s из S пара ( s , s ), очевидно, принадлежит K , т. е. ( s , s ) ϵ K (это означает, что специалист сравнивается с самим собой).

Далее, бинарное отношение K является симметричным отношением, так как для любых объектов s₁ и s 2 из S из того, что пара ( s 1 , s 2 ) принадлежит K следует, что пара ( s 2 , s 1 ) также принадлежит K (в самом деле, если s 1 и s 2 обладают одинаковой компетентностью, то этот факт не зависит от порядка выбора этих объектов).

И последнее: бинарное отношение K является транзитивным, потому что для любых трех объектов s 1 _, s 2 и s 3 из S из того, что пары ( s 1 , s 2 ) и ( s 2 , s 3 ) принадлежат K , вытекает, что и пара ( s 1 , s 3 ) принадлежит K (т. е. если s 1 и s 2 имеют одинаковую компетенцию, а также s 2 и s 3 обладают одинаковой компетенцией, то, конечно, s 1 и s 3 имеют тот же уровень компетентности).

Согласно теории бинарных отношений любое бинарное отношение, обладающее всеми тремя свойствами: рефлексивностью, симметричностью и транзитивностью, является отношением эквивалентности. Отношение эквивалентности является одним из самых фундаментальных понятий во всей математике, так как это отношение, определенное на некотором множестве объектов M , порождает разбиение этого множества на классы эквивалентности.

Теория бинарных отношений подтверждает полученный нами результат. Известно, что если M — произвольное множество объектов, то любое бинарное отношение R на прямом произведении M * M ,задаваемое равенством объектов в том или ином смысле, то есть

R = { ( a, b ): a, b ∈ M , a = b };

всегда является отношением эквивалентности.

Данный результат важен в том смысле, что рассматриваемое отношение эквивалентности K вызывает разбиение множества S на классы эквивалентности таким образом, что каждый объект s из S попадает в один и только один класс. Другими словами, каждый класс содержит только эквивалентные (равносильные) в заданном смысле объекты. Поэтому они и называются классами эквивалентности.

Итак, введенное нами бинарное отноше- ние K с необходимостью разбивает все множество S обучаемых специалистов на непересека-ющиеся классы. В содержательном смысле это означает разбиение на классы, содержащие специалистов с одинаковым уровнем компетенции.

Но теория не отвечает на вопрос, как это разбиение осуществляется. На практике такое разбиение можно осуществить таким образом: выбираются некоторые критерии «эквивалентности» объектов (определяемые природой самих объектов и изучаемых отношений между ними) и в соответствии с ними и проводят разбиение всего исходного множества S на не-пересекающиеся подмножества.

Оказывается, что в соответствии с теорией бинарных отношений любое разбиение множества S на непересекающиеся подмножества порождает отношение эквивалентности на множестве S * S . Возникает принципиальный вопрос: как осуществить такое разбиение исходного множества S, чтобы порождаемое им отношение эквивалентности совпадало с заданным бинарным отношением K ?

Этот вопрос связан с проблемой градации специалистов по уровню их компетентности: как оценить уровень компетентности специалиста, сколько должно быть классов эквивалентности и каковы должны быть их границы?

Оценивание уровня компетентности специалиста зависит от многих факторов, среди которых есть и случайные факторы, поэтому решение этой проблемы, естественно, должно опираться на статистические и вероятностные методы.

Один из возможных подходов состоит в следующем: представим компетентность специалиста с номером i как n — мерный вектор ( xi , xi ,…, xi ), где xi_{k —} уровень компетентности i -го специалиста по критерию k ( i = 1, …, | S |; k = 1, …, n ). Здесь | S | — мощность данного множества S специалистов. Для этого надо сначала поставить и решить задачу о выборе набора критериев для оценки компетентности специалиста данного профиля ( V₁ , V₂ ,…, V_n ). Задача объективной оценки уровня специалиста, по существу, многокритериальна и, следовательно, является достаточно сложной. Здесь неизбежны дополнительные исследования.

В частности, к этой задаче можно подойти с позиции дискриминантного анализа. Этот раздел математической статистики содержит статистические методы решения задачи дискриминации (различения) объектов. Такие методы на основе полученных результатов наблюдения или изучения объекта позволяют определить, к какой из нескольких возможных групп объектов принадлежит исследуемый объект. Здесь предполагается, что этот объект случайным образом выбирается из одной из групп. В настоящей работе будем предполагать, что эта проблема решена.

Дальше возникает вопрос о числе классов эквивалентности, на которое нужно разбить исходное множество S специалистов. С нашей точки зрения, это число можно выбирать произвольно, исходя только из принципа целесообразности. В качестве первого приближения можно взять 4–5 классов эквивалентности (то есть 4–5 уровней градации компетентности специалиста). Эти числа вообще являются общепринятыми в мировой практике при той или иной градации профессионального мастерства (в науке, в образовании, в спорте и т. п.). Вводя, например, 4 уровня градации компетентности, можно условно изобразить соответствующее разбиение множества S на классы эквивалентности на рис. 1.

Обучение, естественно, должно быть организовано так, чтобы за разумное время осуществлялся переход от исходного уровня (таким может быть любой из 4-х уровней) к более высокому уровню. В зависимости от целей обучения такое повышение компетенции может ограничиться достижением определенного уровня (например, уровня 3, а не обязательно уровня 4).

Сам непосредственный процесс обучения или переобучения специалистов должен стро-

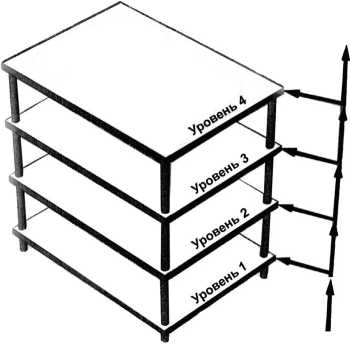
Рис.1. Многослойная инфографическая модель формирования уровней обучения иться, по нашему мнению, на основе современных инновационных технологий контекстного и компетентностного подходов.

Рассмотрим теперь другое бинарное отношение на прямом произведении S * S , где, как и ранее, S — множество обучаемых специалистов. Это бинарное отношение Q зададим с помощью свойства: для любых двух объектов s 1 и s 2 из S пара ( s 1 , s 2 ) принадлежит Q , если s 1 и s 2 обладают «одинаковым» уровнем «интегрального интеллекта».

Под этой характеристикой будем понимать вектор, компоненты которого показывают уровни фундаментального и специального образования специалиста.

Из теории бинарных отношении сразу следует, что введенное нами бинарное отношение Q (так же, как и отношение K ) является отношением эквивалентности. Поэтому, поступая как и ранее, мы получаем разбиение множества S обучаемых специалистов, например, на 4 класса эквивалентности. Эти классы не обязаны совпадать с соответствующими классами эквивалентности по первому признаку разбиения, рассмотренному ранее.

Введем теперь третье бинарное отношение на прямом произведении S * S . Новое бинарное отношение L определим свойством: для любых двух объектов s 1 и s 2 из S пара ( s 1 , s 2 ) принадлежит L , если s 1 и s 2 имеют «одинаковые» способности и мотивацию к обучению.

В силу вышесказанного, это бинарное отношение L также является отношением эквивалентности и порождает новое разбиение множества S обучаемых специалистов на несколько классов эквивалентности (будем исходить из того, что таких классов всего 4). И это новое разбиение множества S не обязано совпадать с двумя предыдущими разбиениями.

По нашему мнению, целесообразно провести дополнительное исследование для выяснения того, насколько сильно скоррелированы между собой эти разбиения по трем приведенным признакам. Если такая «сильная» корреляция имеет место (что мы и предполагаем), то процесс переобучения специалистов существенно упрощается, а следовательно, и удешевляется.

Процесс переобучения специалистов строится на индивидуальном подходе и требует соответствующей настройки интеллектуальной обучающей среды. Это приводит с неизбежностью к большим затратам времени и сил, но далеко не всегда дает ожидаемый результат.

Если наша гипотеза о «сильной» корреляции между тремя изучаемыми разбиениями окажется подтвержденной, то можно ограничиться только 4–5 типовыми настройками интеллектуальной обучающей среды (на каждый класс эквивалент ности разбиения) с достаточно хорошей эффек тивностью переобучения. Такой подход, по су ществу, является квазииндивидуальным.