Структурная модель разрушения минерального агрегата

Горная порода – агрегат, состоящий из кристаллических и аморфных минералов, жидкой и газообразной фазы [1]. Минералы встречаются в основном в виде кристаллов и зерен неправильной формы, поликристаллических масс.

Одной из важнейших характеристик, влияющей на все процессы механического поведения минералов, является трещиноватость – плоский разрыв сплошности среды, в том числе заполненный другим материалом. Агрегаты минералов могут иметь внутрикри-сталлические дефекты размером 10-9 – 10-5 м – трещины первого порядка; трещины между кристаллами порядка 0,1 мм – трещины второго порядка; тектонические трещины отрыва и скалывания – трещины третьего порядка около 1 см и более.

Пористость также оказывает сильное влияние на деформацию и прочность горных

*Работа выполнена при финансовой поддержке аналитической ведомственной целевой программы "Развитие научного потенциала высшей школы" (проект 2.1.2/5135).

пород. Поры бывают субкапиллярные (диаметр пустот менее 10-7 м), капиллярные (10-7 – 10-4 м), сверхкапиллярные (более 10-4 м), форма и размеры пор могут быть самыми различными. На величину пористости существенно влияет взаимное расположение зерен. Под действием давления пористость снижается, происходит выжимание газов из породы, взаимное перемещение частиц (укладка), разрушение структуры и зерен породы.

В последнее время проводятся широкие исследования внутреннего механизма деформирования горных пород – развитие физики горных пород (рентгенография, электронная микроскопия) и теории трещинообразования. Экспериментально установлено, что деформирование горных пород определяется закрытием внутренних микротрещин и пор, деформированием минерального скелета, образованием и раскрытием микротрещин. Деформация горных пород как минеральных агрегатов определяется деформацией минеральных зерен и межзеренных границ, их размерами, контактами, ориентацией [2].

Разрушение горных пород начинается обычно по границам минеральных зерен. Начало образования трещин наблюдается при уровне нагрузок меньше предела мгновенной прочно- сти и соответствует пределу длительной прочности пород на одноосное сжатие. Механизмы зарождения, развития и ветвления микротрещин, образования макротрещин определяются локальными свойствами микрообъема. Поэтому особый интерес представляет установление критериев образования и развития микротрещин на уровне минеральных зерен.

Существуют различные подходы к построению структурных моделей различных материалов (в частности, горных пород) – используются методы механики композиционных материалов [3], учета влияния микронеоднородностей на локальные напряжения и их релаксацию [4], статистические методы [5], теория протекания [6], теория фракталов [7], анализ структурных сдвиговых механизмов [8], метод подвижных клеточных автоматов [9].

В данной статье развивается подход, основанный на анализе условий вязкопластического деформирования межзеренных границ минерального агрегата, предложен новый критерий формирования макротрещины в представительном элементе геоматериала, в качестве примера применения модели дана оценка предела прочности образцов сильвинита.

• 2.    Одноосное сжатие

Пусть геоматериал состоит из зерен неправильной формы с разнообразно ориентированными гранями и межзеренным пространством, называемым контактом. Характерная длина грани контакта l , а h – его толщина. Показатели механических свойств контактов на порядок ниже соответствующих характеристик зерен, поэтому полагаем, что зерна деформируются упруго, а контакты испытывают вязкопластическую деформацию.

Пусть начало вязкопластического деформирования контакта связано с выполнением условия, аналогичного критерию Кулона τ_α = τ ₀ + k σ_α ,          (1)

где τ_α , σ_α – касательное и нормальное напряжение на контакте, расположенном под углом α к оси x ; τ – сцепление; k = tg ϕ ; ϕ – угол внутреннего трения.

Рассмотрим одноосное сжатие представительного элемента геоматериала, содержащего достаточно много зерен и контактов (рис. 1), в направлении оси y .

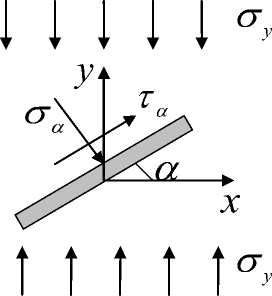
Рис. 1. Схема одноосного сжатия отдельного контакта минерального агрегата

Нормальное и касательное напряжения на контакте выражаются как

σ_α = σ _y cos² α , τ_α = (1/ 2) σ _y sin 2 α .    (2)

Тогда критерий (1) преобразуется к виду

σ ′ _yf ( α ) = 1 , f ( α ) = cos² α ( tg α - k ), (3)

где σ ′ _y = σ _y / τ ₀ .

При заданном параметре k с ростом безразмерной нагрузки σ′ вязкопластическая деформация начнется на контакте, расположенном под некоторым критическим углом α* ,  доставляющим максимум функции f (α) . Зависимость критического угла начала вязкопластического деформирования α* от угла внутреннего трения является линейной:

α ^* = π /4 + ϕ /2 .          (4)

Зависимость критического угла α ^* от параметра k показана на рис. 2.

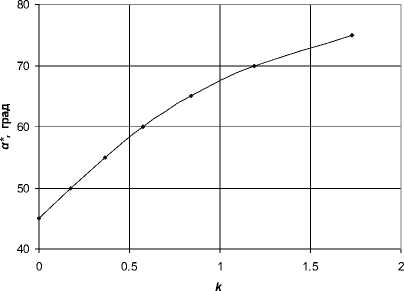
Рис. 2. Зависимость критического угла начала вязкопластического деформирования (разрушения) контакта от параметра k

Предполагается, что при выполнении условия (1) или (3) на контакте возникает скольжение одного берега контакта относительно другого, причем максимально возможное относительное перемещение Δ u ^m , определяемое присутствием жестких окружающих зерен, будет пропорционально толщине контакта:

Δ u τ ^m = λ h ,             (5)

где λ – параметр, отражающий геометрию (форму) зерна.

С помощью проекций перемещения Δ u _τ ^m на оси координат Δ u ^m = Δ u^m cos α ^* и Δ u^m = Δ u^m sin α ^* можно ввести максимальные неупругие деформации, вызванные скольжением вдоль контакта:

ε ^m = Δ u^m / l = λ ( h / l )cos α ^*,

ε ^m =Δ u^m / l = λ ( h / l )sin α ^* .     (6)

Поскольку речь идет о вязкопластическом деформировании, то эти максимально возможные неупругие деформации, обусловленные относительным смещением границ контакта, достигаются в течение некоторого времени, т.е. деформирование осуществляется с конечной скоростью, например по закону

ё = kp« - ^x), гьр = kpёт -ё),          (7)

где ε ^p , ε ^p – текущие неупругие деформации области контакта.

При заданном уровне нагрузки σ ′ _y уравнения (7) интегрируются:

ε _x ^p = ε _x ^m (1 - exp( - k_pt )) ,

ε y^p = ε y^m (1 - exp( - kpt )),         (8)

где t – время.

Решение (8) отражает этап ограниченной ползучести для отдельно взятого контакта.

• 3.    Критерий образования макротрещины

Если уровень нагрузки σ ′ значительный, то условие (1) или (3) будет выполняться уже для контактов с различной ориентацией в некотором интервале углов Δ α = α - α , включающем предельный угол α ^* .

Введем плотность распределения контактов по углу ориентации n ( α ) так, что dN = n ( α ) d α – количество контактов, попавших в интервал углов d α . Пусть условие

(1) или (3) выполнилось для всех контактов с ориентацией углов, лежащих в интервале (α ,α ) . Тогда количество контактов, распо- ложенных в этом интервале углов, определяется

α ₂

так: N = ∫ n ( α ) d α , причем каждый из них α ₁

вносит свой вклад в неупругие деформации: α ₂

ε ^m = ∫ ( ∆ u^m / l ) n ( α )cos α d α , α ₁

α ₂

ε ^m = ∫ ( ∆ u^m / l ) n ( α ) sin α d α .     (9)

α ₁

В выражениях (9) величина относительного скольжения и длина контакта в общем случае также зависят от угла ориентации. Ограничимся здесь более простым вариантом полагая их постоянными. Более того, будем полагать равномерным распределение количества контактов по углу n(α) = n = const , тогда получим простые соотношения εm = λn(h/l)(sin α - sinα ) , εm = λn(h/l)(cosα -cosα ).   (10)

Согласно (9) предельная неупругая деформация представительного элемента определяется геометрией (длиной и шириной) контакта, функцией плотности распределения контактов по углу, структурным параметром, величиной углового сектора, в котором контакты испытывают неупругую деформацию (зависит от уровня нагрузки, механических свойств контакта).

При увеличении уровня внешней нагрузки σ ′ _y , если на соседних контактах, ориентированных произвольным образом, будут реализованы условия течения (3), области неупругого деформирования могут объединиться в виде ломаной линии (поверхности) – макротрещины, это может привести к разрушению представительного элемента. При неупорядоченном (хаотичном) расположении граней зерен (контактов) вероятность возникновения трещины возрастает с увеличением интервала углов ( α , α ) , для которых выполняется критерий (3). Поэтому в качестве критерия разрушения (образования макротрещины) примем следующее условие:

Δ α = α ₂ - α ₁ =Δ α _max,      (11)

где Δαmax– предельное значение интервала углов.

Зависимость диапазона углов, в котором выполняется условие начала вязкопластического деформирования, от уровня безразмерной нагрузки показана на рис. 3. Чем больше угол внутреннего трения, тем меньше диапазон углов (меньше количество контактов) при заданном уровне нагрузки, где выполняется условие (3).

Зависимость уровня нагрузки, при котором возникает макротрещина, от угла внутреннего трения для заданных значений предельного значения интервала углов ( Δ α _max = 20 ° – кривая 1, 30 ° – кривая 2) показана на рис. 4.

σ y

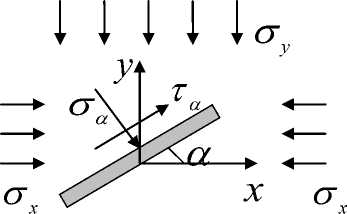
Рис. 5. Схема двухосного сжатия отдельного контакта минерального агрегата

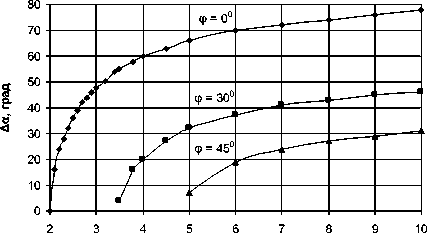
Рис. 3. Зависимость диапазона углов, в котором выполняется критерий (3), от уровня относительной нагрузки σ ′

4. Двухосное сжатие

Рассмотрим двухосное сжатие представительного элемента геоматериала (рис. 5).

Нормальное и касательное напряжения на контакте определяются так:

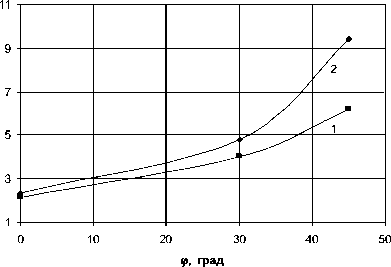
Рис. 4. Зависимость относительной нагрузки σ ′ , вызывающей образование макротрещины, от угла внутреннего трения для двух значений предельного интервала углов

σ = σ cos² α + σ sin² α ,

α y            x

τ_α = ¹ ( σ _y - σ _x )sin2 α       (12)

Условие Кулона (1) запишется в форме σ ′ _y [ (1 - λ _x )(sin2 α - k cos2 α ) - k (1 + λ _x ) ] = 1 , (13) где λ _x = σ _x / σ _y – коэффициент уровня боковой нагрузки.

Критерий (13) выполнится с ростом нагрузки σ ′ первоначально для некоторого угла α ^* , который, как и для одноосного сжатия, связан с углом внутреннего трения ϕ зависимостью (4).

При условии k = 0 критерий (13) дает следующее выражение для напряжения, приводящего к появлению первоначальных неупругих сдвиговых деформаций на контакте под углом α ^* = π /4 :

σ ′ y = 2/(1 - λ x ) .               (14)

Условие появления первых сдвигов на кон-

тактах под углом α ^* , определяемым выражением (4), в общем случае записывается в форме

σ ′ y

2cos ϕ

1 - λ _x - (1 + λ _x )sin ϕ

Зависимость а' (A x ) для различных углов внутреннего трения ф показана на рис. 6.

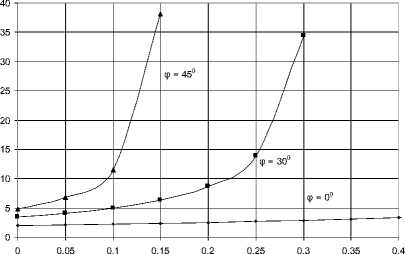
Рис. 6. Зависимость относительной нагрузки σ ′ , необходимой для появления неупругих деформаций на контакте, от коэффициента уровня боковой нагрузки λ _x

Итак, если при условии k = 0 напряжение а у неограниченно возрастает при коэффициенте A ^ 1 (формула (14)), то для ненулевых углов внутреннего трения это происходит значительно раньше. Величина а У ^ да при A x = 1/3 (для ф = 30°), A x = 0,17 (для ф = 45°).

Таким образом, при двухосном напряженном состоянии для появления неупругих деформаций на контактах (тем более для разрушения представительного элемента) необходимы значительные нагрузки, так как даже небольшое боковое давление при ненулевых углах внутреннего трения оказывает значительное влияние на критерий (15). При напряженном состоянии, близком к объемному напряженному состоянию, условия появления неупругих деформаций в представительном элементе минерального агрегата могут вообще не реализоваться. В действительности наблюдается объемная ползучесть, обусловленная прежде всего наличием пористости.

• 5.    Оценка предела прочности образцов сильвинита с помощью структурной модели

Рассмотрим применение полученных соотношений к сжатию образцов геоматериала различной геометрии h / d . Авторами [10] при решении упругой задачи были получены средние по образцу относительные показате- ли напряженного состояния, которые применительно к данной задаче можно записать в виде

{а = 0,425 - 0,36 • ( h / d) + 0,075 • ( h / d )², (ay) = 1,325 - 0,30 • ( h / d ) + 0,075 • ( h / d )² (16)

Из выражения (16) можно оценить средний коэффициент уровня боковой нагрузки A = ( a У ( a) Для различной геометрии: A_x = 0,0048 ( h / d = 2); A_x = 0,127 ( h / d = 1); A _x = 0,221 ( h / d = 0,5). Теперь, применяя формулу (15), получим для угла внутреннего трения ф = 30° величины относительного сжимающего напряжения, требуемого для появления неупругой деформации по всему объему образца: а у = 3,52 ( h / d = 2); а у = 5,60 ( h / d = 1); а у = 10,28 ( h / d = 0,5).

В работе [11] получено значение предела текучести при сдвиге межзеренных границ в сильвините с помощью прибора NanoTest-600 т = 2,5-4,0 МПа. Тогда абсолютные значения сжимающего напряжения, приводящего к неупругим деформациям образца сильвинита, определяются как а _у = 8,8-14,1 МПа ( h / d = 2); а _у = 14,0-22,4 МПа ( h / d = 1); а _у = 25,7-41,1 МПа ( h / d = 0,5).

Отметим, что при этих напряжениях происходит неупругое деформирование образца в большом объеме, сравнимом с размерами самого образца. Переход в неупругий режим в локальных областях осуществляется при значительно более низких напряжениях (менее 2-3 МПа) - это показывают эксперименты по сжатию-разгрузке образцов.

Полученные значения хорошо коррелируют с величинами предела прочности при сжатии образцов сильвинита а пр [12]. Из модели следует, что величина а'_у очень чувствительна к значению угла внутреннего трения ф материала контакта (межзеренной границы).

Кроме того, следует отметить, что в качестве оценки бокового давления в представительном элементе использовалась процедура усреднения напряженного состояния в целом по образцу.

• 5.    Заключение

Представлена структурная модель отдельного межзеренного контакта минерального агрегата, позволяющая сформулировать простые условия возникновения неупругого деформирования контакта и перехода к появлению макротрещины – разрушению представительного элемента. Показано, что предельные нагрузки, приводящие к разрушению представительного элемента, определяются геометрией (длиной и шириной) контакта, функцией плотности распределения контактов по углу, структурным параметром, углом внутреннего трения материала контакта.

Развитие данной модели предполагает переход к рассмотрению общего пространственного случая, а также локальных напряжений на контакте.

В заключение автор выражает искреннюю благодарность профессору С.А.Кон-стантиновой за обсуждение постановки задачи и результатов исследований.