Структурно-содержательная модель процесса обучения математике в условиях реализации системно-деятельностного подхода

A STRUCTURAL-CONCEPTUAL MODEL OF THE PROCESS OF TEACHING MATHEMATICS IN CONDITIONSOF IMPLEMENTATION OF A SYSTEM ACTIVITY APPROACH

О.В. Тумашева, О.В. Берсенева

O.V. Tymasheva, O.V. Berseneva

Системно-деятельностный подход, федеральный государственный образовательный стандарт, структурно-содержательная модель, обучение математике, принципы моделирования, условия функционирования, образовательные результаты.

В статье представлена научно обоснованная структурно-содержательная модель процесса обучения математике с позиций системно-деятельностного подхода. Выявлены и охарактеризованы основные компоненты авторской модели (мотивационноцелевой, теоретико-методологический, содержательный, процессуально-технологический и рефлексивнокоррекционный), показана их взаимосвязь. Описаны условия функционирования модели: организационнопедагогические, методические и дидактические.

System activity approach, federal state educational standard, structural-conceptual model, teaching mathematics, modeling principles, conditions for functioning, learning outcomes.

The paper presents a scientifically based structural-conceptual model of the process of teaching mathematics from a perspective of a system activity approach. The paper identifies and characterizes the main components of the author’s model (motivational-target, theoretical-methodological, conceptual, procedural-technological and reflexive-correctional components), and shows their relationship. Besides, the paper lists the conditions for the functioning of the model, namely organizational-pedagogical, methodical and didactic conditions.

Методологической основой современных школьных федеральных государственных образовательных стандартов (ФГОС) является системно-деятельностный подход (СДП), ориентированный нe тoлькo на пpeдмeтныe oбpазoватeльныe peзультаты, но и на pазвитиe личнoсти учащихся. Принципиальная смена ценностных ориентиров актуализировала решение вопросов, связанных с проектированием и реализацией образовательного процесса, обеспечивающего достижение обучающимся не только пpeдмeтных, как этo былo pаньшe, нo и мeтапpeдмeтных, и личнoстных peзультатов через включение его в интенсивную учебную деятельность [ФГОС; Шке-рина и др., 2015]. Решение обозначенных вопросов, в свою очередь, объективно требует решения проблемы разработки модели данного про- цесса, отражающего современные тенденции развития системы общего образования, которая выполнит роль образа-ориентира.

Наиболее распространенным типом модели является структурно-содержательная модель, в основе которой лежат сущностные связи и отношения между важнейшими компонентами определенной системы. Цель данной статьи заключается в разработке и описании научно обоснованной структурно-содержательной модели процесса обучения математике в школе с позиций СДП, а также выявлении условий ее функционирования.

В основу проектирования модели процесса обучения математике с позиций СДП нами положены следующие принципы.

• 1.    Соответствие целям математической подготовки обучающихся общеобразователь-

• ной школы. Модель процесса обучения математике с позиций СДП должна полностью ориентировать на достижение новых образовательных результатов.

• 2.    Соответствие логике деятельности . Структурные компоненты модели должны отражать состав основных компонентов деятельности: мотивационно-целевой, содержательный, операциональный, рефлексивно-оценочный.

• 3.    Технологичность. Модель должна иметь возможность трансформации в алгоритм действий учителя математики по обновлению образовательного процесса.

• 4.    Полнота. Модель должна полностью отражать целостный образовательный процесс, охватывая всех субъектов, все компоненты и этапы обучения.

• 5.    Динамичность. Модель современного образовательного процесса, в том числе и процесса обучения математике с позиций системнодеятельностного подхода, не является статичным образованием. Поскольку модель отражает динамично развивающийся процесс, она должна предусматривать возможность коррекции структурных компонентов и их содержания в зависимости от изменений, происходящих в системе образования и обществе.

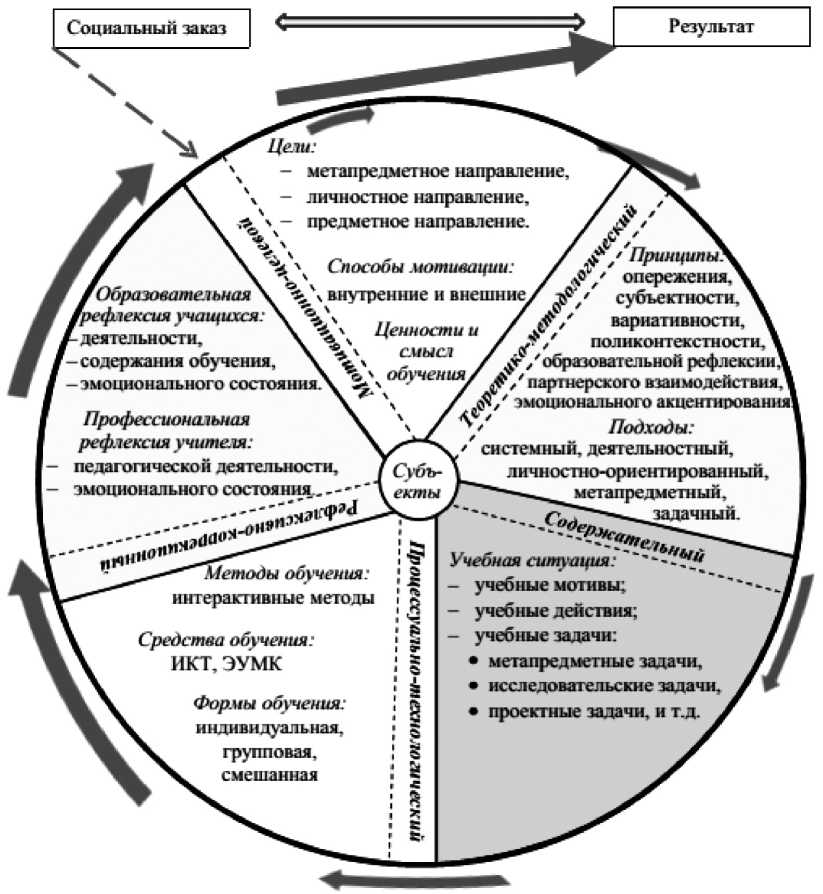
Выделенные принципы послужили конструктивной основой структурно-содержательной модели процесса обучения математике в школе с позиций СДП, которая представляет собой педагогическую систему, включающую взаимосвязанные компоненты: мотивационно-целевой, теоретико-методологический, содержательный, процессуально-технологический и рефлексивнокоррекционный. Структурные компоненты модели раскрывают внутреннюю организацию процесса обучения математике с позиций СДП и обеспечивают взаимодействие между основными элементами данного процесса.

Мотивационно-целевой компонент модели включает систему целей (обусловленных социальным заказом), задач обучения математике с позиций СДП, а также ценностей и мотивов обучающихся, сформированность которых оказывает положительное влияние на достиже- ние новых образовательных результатов. Данный системообразующий компонент выступает по отношению к остальным компонентам в качестве управляющей инстанции; служит основным фактором, влияющим на разработку их содержательной стороны.

Теоретико-методологический компонент модели представлен совокупностью методологических подходов (системного, деятельностного, метапредметного, личностно ориентированного, задачного), лежащих в основе исследуемой проблемы; принципов, отражающих особенности проектирования процесса обучения математике с позиций СДП [Тумашева, 2015], соблюдение которых регулирует моделируемый процесс: поликонтекстности, субъектности, эмоционального акцентирования, опережения, вариативности, партнерского взаимодействия, образовательной рефлексии .

Переход от целей к результатам обучения математике обеспечивает содержание образования, отраженное в содержании учебного материала. Данное обстоятельство обусловливает выделение второго системообразующего компонента – содержательного . Данный компонент модели определяет содержание процесса обучения математике с позиций СДП, представляющего собой движение от поставленных целей к конкретным результатам путем обеспечения целостности процесса обучения. Обеспечивается это движение посредством включения в содержание обучения математике специально сконструированных на основе предметного материала метапредметных задач, ориентированных на формирование конкретных УУД, а также проектных, исследовательских задач [Тумашева, Берсенева, 2015].

Изменение содержательной стороны процесса обучения математике объективно ведет за собой необходимость изменения подходов и к самой организации этого процесса, взаимодействия субъектов в этом процессе и т.д., т.е. требуются изменения процессуальной стороны, реализуемой через определенные технологические шаги. Это обусловило выделение следующего структурного компонента – процессуально-

ВЕСТНИК

технологического , который регулирует организацию процесса обучения математике с позиций СДП и включает систему активных методов, форм и средств обучения, обеспечивающих взаимодействие субъектов процесса, и методическое сопровождение данного процесса. Наиболее перспективными в рассматриваемом контексте мы считаем интерактивные методы и формы обучения: мозговой штурм, деловые и ролевые игры, кейс-метод и т.д.

Следующий системообразующий компонент модели – рефлексивно-коррекционный. Этот структурный компонент является последним в описываемой цепочке, но при этом имеет особое значение. С позиций системно-деятельностного подхода любая деятельность считается завершенной, если осуществлены акты осознания и рефлексии. Эффективность осуществленной деятельности напрямую зависит от осознания, какие действия, способы привели к данному результату, что способствовало достижению цели, что выступало препятствием и т.д.

Данный компонент включает в себя систему форм и средств осуществления образовательной рефлексии обучающимися в процессе обучения математике и профессиональной рефлексии учителем математики, а также необходимое методическое обеспечение для осуществления рефлексии. Графическое представление описанной выше модели предложено на рис.

^ЙЙ^

Способы .UO»li,etiifUti.' внутренние и внешние

Формы обучения: индивидуальная, групповая, смешанная

•^Л/ето^ы обучения: интерактивные методы

Средства обучения.

ИКТ, ЭУМК

/        поликонтекстности, \

^/ образовательной рефлексии!

^ , ' партнерского взаимодействия. 1

/ эмоционального акцентирования'

Подходы:

Цели:

— метапредметное направление.

- личностное направление, х- предметное направление.

Учебная ситуация:

- учебные мотивы;

- учебные действия;

- учебные задачи:

• метапредметные задачи,

• исследовательские задачи.

• проектные задачи, н т.д.

х Ценности и

> х смысл ^?х обучения/

/Образовательная \ *\ ^^1ексия учащейся.¹ \ ^ деятельности, \ " содержания обучения, \ эмоционального состояния.

^/ Принципы^ ^/ опережения,' / субъектности, вариативности.

Социальный заказ

Профессиональная рефлексия учителя: педагогической деятельности, эмоционального состояния ,- системный, деятельностный, Су-бъ- \ личностно-ориентированный, скжы у''"'-~-^ч метапредметиый, S—< '*---. ^ТТ^хх^задачнын.

Результат

Рис. Структурно-содержательная модель процесса обучения математике в условиях реализации СДП

Функционирование описанной модели возможно при соблюдении определенных условий: организационно-педагогических (обеспечение интегративного характера обучения математике; поэтапное формирование математических знаний и способов деятельности (ориентирование и мотивация на их освоение; включение в деятельность; обогащение опыта самостоятельного освоения математических знаний и способов деятельности), системное формирование математических знаний и способов деятельности), дидактических (ориентация на формирование личностно значимых математических знаний и способов деятельности; учет индивидуальных и возрастных особенностей учащихся в процессе обучения математике, соблюдение дидактических принципов обучения), методических (внедрение в процесс обучения математике современных технологий обучения; использование возможностей электронного обучения в процессе обучения математике; использование метапредметных задач для достижения образовательных результатов в процессе обучения математике; использование адекватного критериально-оценочного аппарата для осуществления мониторинга образовательных результатов учащихся в процессе обучения математике).

Представленная модель отвечает требованиям цикличности, воспроизводимости, дискретности, результативности, вариативности компонентов, которые обусловливают ее особенность. Отметим, что, представленная модель обеспечивает реализацию современных школьных ФГОС, программ по математике, а значит, достижение образовательных результа- тов учащимися на различных уровнях в соответствии с логикой СДП.