Светящийся столб градиента температура в воздухе

Введение.

“Появляясь в воздухе при замерзании водяных капелек, ледяные кристаллы принимают обыкновенно одну из трех форм шестисторонних правильных призм: призмы, в которых длина очень велика по сравнению с их сечением; это (фиг.Ана черт. 1) — всем известные ледяные иголочки, в морозные зимние дни массами реющие в самых нижних слоях атмосферы. Падая свободно в воздухе, такие иголочки располагаются длинной осью вертикально. Плоскости этих кристаллов, которые кружась, постепенно опускаются на землю, большую часть времени ориентированы параллельно поверхности. На восходе или закате, луч зрения наблюдателя может проходить через эту самую плоскость, и каждый кристалл может вести как миниатюрная линза, преломляющая солнечный свет.

Световой , или солнечный , столб представляет собой вертикальную полосу света, тянущуюся отсолнцаво время заката или восхода. Явление вызывается шестиугольными плоскими либо столбовидными ледяными кристаллами. Подвешенные в воздухе плоские кристаллы вызывают солнечные столбы, если солнце находится на высоте 6 градусов над горизонтом, либо позади него, столбовидные — если солнце находится на высоте 20 градусов надгоризонтом. Кристаллы стремятся занять горизонтальную позицию при падении в воздухе, и вид светового столба зависит от их взаимного расположения.” ( Калужский государственный педагогический, университет им. К.Э. Циолковского, Кафедра физики, Оптические явления в атмосфере, Калуга, 2009 )

Мне было трудно представить себе, что поголовно все кристаллы заняли абсолютно горизонтальную позицию при падении в воздухе.

Я ехал в Нягань из Тюмени. На машине, зимой, поздно вечером. В машине был наружный датчик температуры. На вершине горки было -38,50С, в низине до -41,50С. Таким образом, в воздухе имело место градиент направления температуры с увеличением высоты.

А сейчас рассмотрим результат градиента температуры в воздухе. Термодинамика в атмосфере.

В термодинамике существует формула:

P*V = m * RT.

ц

Преобразуем формулу (1) в другой форме:

Pm

=      * R.(2)

T

Окончательно переформулируем в виде:

р =  Ср ----, где р - плотн., Ср - Const.(3)

В обычной погоде, справедливы формулы зависимости давления и температуры от высоты:

P(h)=Po(1 - C*h) T(h)=To(1 - C*h) ,где h - высота от земли

В этом случае, можно полагать такую зависимость плотности от высоты (что здесь справедливо на какую-то высоту):

р(к) ~ Const(5)

Когда же температура растёт с высотой, т.е. T(h)=T₀(1 + C_T*h) , то зависимость плотности от высоты будет падать (даже и быстрее чем давление):

рф) = ро (1 - C*h)(6)

Рассмотрим об отражении и преломлении в атмосфере при имеющем градиенте плотности.

Отражение и преломление.

Как указывается в справочнике относительным покозателем преломления n₂₁ второй среды относительно первой называется отношение фазовых скоростей света v 1 и v₂ соответственно в первой и второй средах:

v1

n21 =          =         ,(7)

v2

где n 1 и n₂ - абсолютные показатели преломления первой и второй сред.

Имеет место справедливости формулы Френеля:

sin а

= (8)

sin в

Коэффициент отражения s-поляризация sin2(a - в)

Rs =-----2 (9)

sin ( а + в )

Коэффициент пропускания s -поляризация

TS = 1 - RS(10)

Коэффициент отражения p -поляризация

R P

tg2(a - в)

tg²( a + в )

Коэффициент пропускания p-поляризация sin2a* sin2p

Tp =___________________ sin2(a + P)*sin2(a -p)

В важном частном случае нормального падения света исчезает разница в коэффициентах отражения и пропускания для p - и s -поляризованных волн.

Для нормального падения:

Коэффициент отражения

R s   = I

n 0 – n 1

n 0 + n 1

I

Коэффициент пропускания

4n 0 n 1

T s =--------2-

(n 0 + n 1 )²

“(Mirage, Luftspiehelung) — атмосферическое явление, благодаря которому при известных обстоятельствах делаются в какой-либо местности видными предметы, действительное местонахождение которых вдали от места их наблюдения зрителем. Оно объясняется полным отражением лучей на границе двух слоев воздуха, имеющих различные температуры, если луч света падает с очень сильным наклоном на граничную плоскость.

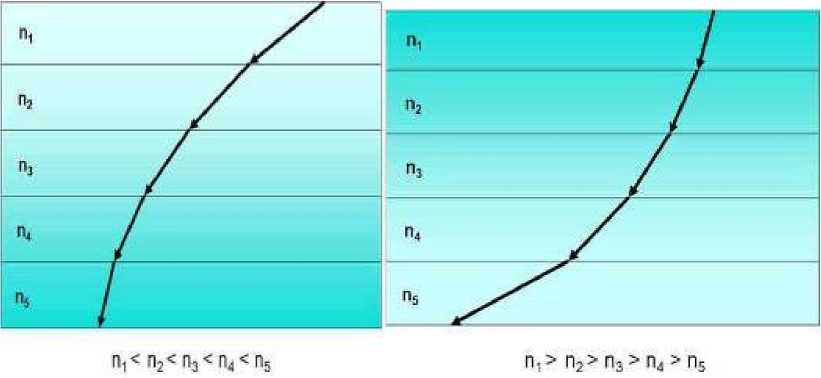
Рис. 1. А. Б.

Если зритель и отдаленный предмет находятся на лишь немного повышенных точках и между ними лежит сильно нагретая солнцем песчаная почва, сообщающая свою теплоту ближайшим слоям воздуха и тем нагревающая их сильнее слоев, выше расположенных, зритель видит предмет в его действительном положении при посредстве лучей, прямо от предмета идущих к нему, и во-вторых, в перевернутом положении, при посредстве лучей, сначала идущих от предмета книзу, потом, при встрече с более теплыми и поэтому более редкими слоями воздуха, подвергающихся отражению и идущих к глазу наблюдателя, видящего предмет как бы отраженным в воде. Это объяснение дал еще Монж в "M é moires de l'Institut d'Egypte". Если сильно нагретый теплый слой не внизу, но вверху наблюдателя и наблюдаемого предмета, находящихся в более плотном холодном слое, — может также получиться явление миража, но только по направлению кверху.” ( Калужский государственный педагогический, университет им. К.Э. Циолковского, Кафедра физики, Оптические явления в атмосфере, Калуга, 2009 )

Пусть, два таких слоёв с различными температурами с одной границей.

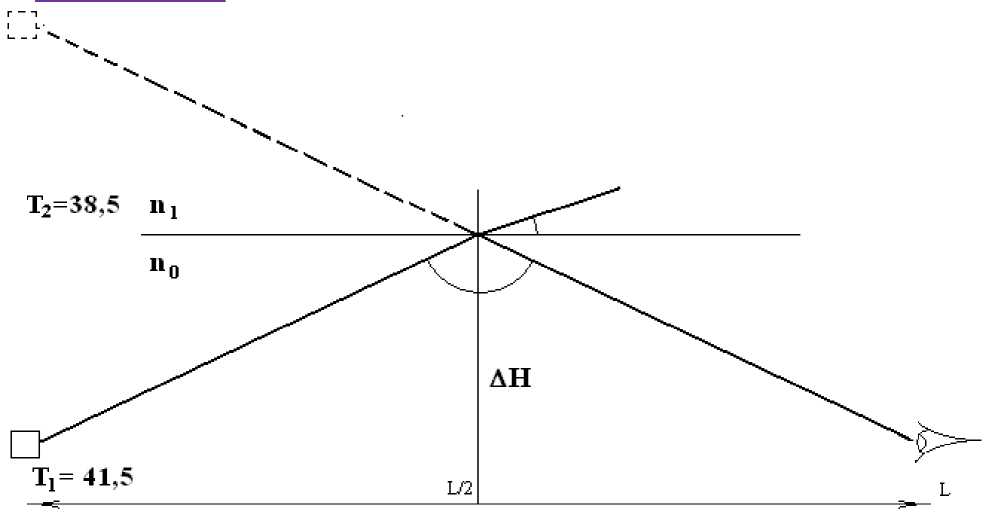
Рис.1

R 1   =  |

n 0 – n 1

n 0 + n 1

|

T 1

4n 0 n 1

(n 0 + n 1 )²

Теперь, пусть две границы на три слоя.

R 1

R 2

2 n 0 – n 1

n 0 + n 1

n 1 – n 2

n 1 + n 2

T 1

T 2

4n 0 n 1 (n 0 + n 1 )²

4n 1 n 2 (n 1 + n 2 )²

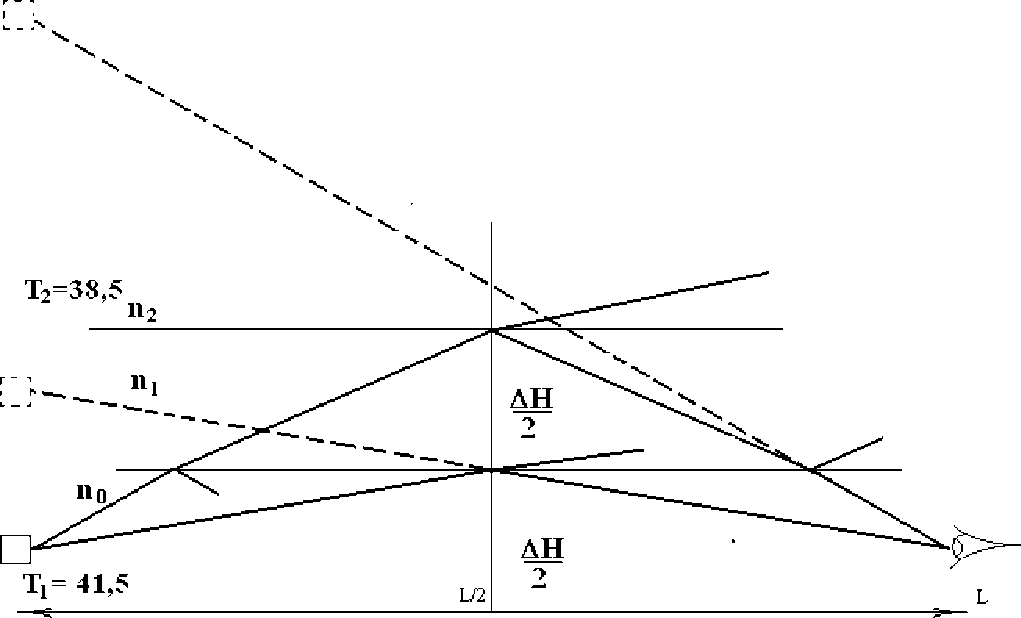
А теперь куча таких границ.

R 1   =	n 0 – n 1        2                        4n 0 n 1 |                       |                     T 1   =                   2 n 0 + n 1                                 (n 0 + n 1 )2
R 2   =	n 1 – n 2        2                        4n 1 n 2 2                         2 n 1 + n 2                                (n 1 + n 2 )
R 3   =	n 2 – n 3        2                        4 n 2 n 3                      (17) |                       |                     T 3   = n 2 + n 3                                (n 2 + n 3 )2
… …	…          …     …
R k =	n k-1 – n k        2                         4 n k-1 n k |                     |                    T k =                   2 n k-1 + n k                               (n k-1 + n k )

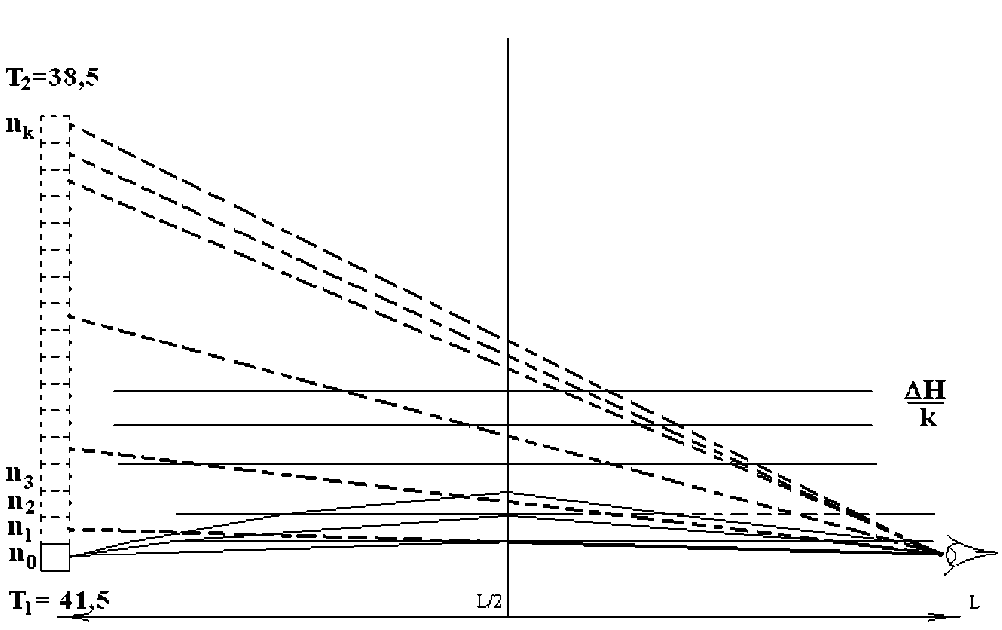
Выбираем такие слои, когда n i = n_o A _o i . Тогда

R i   =   |

n0A0i 1 - n0A0i        । n0A0i 1 + n0A0i

T i

^{4 n}0 ^A 0i ^{1 n}0 ^A 0i (n o A oi ¹ + n o A oi )²

т.е., сократив всё, получаем:

1 - A o

R i   =  |        1 + A _o       ।

T i

4 A o (1 + A o ) 2

Далее, если продолжить, то можно допустить удвоение слоёв. При этом, если светимость отражений уменьшится вдвое, но теперь и отражений тоже будет вдвое больше, т.е. будут накладываться друг не друга. Таким образом, в пределе, при каком-то градиенте, получается видимый световой столб, не имеющий расширения, а просто затухающий с высотой.

Видел над факелами и фонарями световой столб в сильный мороз.

Из всех фоток про световые столбы, на котором видны звёзды в небе, в указанном нет никакого смысла говорить о явлении, которое вызывается шестиугольными плоскими либо столбовидными ледяными кристаллами. Очевидно, что имеет смысл исключительное значение градиента плотности (или градиента скорости света в среде).

Заключение.

Разумеется, что высказанное об этой моей статье о градиенте температуры, не самым лучшим, в силе о моей инвалидности. По крайней мере, эта статья явно недостаточна. У меня вообще всё очень плохо пишется. Но ведь найдётся хоть кто-нибудь, кто либо разгромит эту статью (ткнув пальцем в конкретной формуле на конкретное значение), либо будет более обширно и грамотно её использовать.