Свободное движение пятиточечной стержневой большой орбитальной космической системы цепочечной структуры в транспортирующей системе координат

Особенностью поведения космических систем рассматриваемого вида является хаотический характер вращательных движений стержней в механической системе с большим числом степеней свободы. На параметры этого движения определяющее влияние оказывают массы точек, длины стержней, нелинейность гравитационного поля и дифференциальных уравнений движения системы и, естественно, начальные условия при численном моделировании.

В работе [4, 5] авторами построена математическая модель динамики пятиточечной стержневой большой орбитальной космической системы (БОКС).

Исследование 5-массовой БОКС в транспортирующей системе координат

Предполагается, что рассматриваемая система состоит из n + 1 материальных точек,

соединенных шарнирно-последовательно в цепочку n невесомыми стержнями.

Система совершает свободное движение в орбитальной плоскости под действием центральной ньютоновской силы. Для изучения динамики БОКС при численном моделировании принято:

• –    массы материальных точек (шарниров) одинаковы и равны m , количество точек – пять;

• –    длины четырех стержней одинаковы и равны l (при этом 4 1 <<  H , где H - начальная высота точки M ₁ над поверхностью Земли);

  – для анализа относительного движения введена подвижная поступательно движущаяся система координат M ₁ xy – транспортирующая система координат (ТСК) [1–3];

• –    начало ТСК совпадает с опорной точкой О , в качестве которой принята первая точка M ₁ пятиточечной БОКС;

• –    начальная скорость опорной точки соответствует ее местной круговой скорости

  ^u 0 =

  
  

  у M

  
  

  \ R 3 + H

  
  

где R ₃ – радиус Земли;

• –    начальные абсолютные угловые скорости всех стержней нулевые, т.е. БОКС в начальный момент движется мгновенно-поступательно;

• –    оси Ox и Oy транспортирующей системы координат в начальный момент совпадают с осями орбитальной системы координат опорной точки, т.е. ось Ox направлена по местной горизонтали против вектора скорости опорной точки, а ось Oy по местной вертикали;

  – в начальном положении пять точек БОКС расположены на дуге полуокружности в первой четверти ТСК, первая точка – опорная находится в начале координат, пятая – на оси Oy (рис. 1);

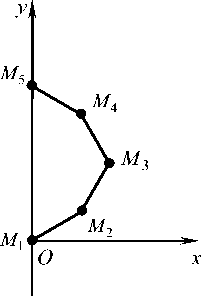
Рис. 1. Начальное положение БОКС в ТСК

• –    время свободного движения БОКС соответствует двум оборотам системы вокруг опорной точки, что соответствует одному обороту вокруг гравитационного центра.

Результаты исследования приведены на рис. 2, 3, где показаны 25 положений точек системы в ТСК через равные (473 с) промежутки времени на первом (рис. 2) и втором (рис. 3) оборотах БОКС относительно опорной точки. Спиральной линией с угловыми точками возврата отмечены угловые положения первого стержня БОКС, соединяющего первую (опорную) и вторую точки цепочки. Угловые точки на спирали соответствуют обращению в ноль угловой скорости первого стержня и, соответственно, изменению направления вращения его в абсолютном пространстве. Всего таких изменений на рассмотренном интервале времени – восемь:

первые два на первом обороте БОКС, следующие шесть – на втором.

Траектория пятой, концевой, точки цепочки отмечена стрелочками. Эта траектория, если судить по полярному углу пятой точки относительно первой, является незамкнутой. Расстояние r _1,5 между этими точками в течение первого оборота меняется от r max « 4 1 до

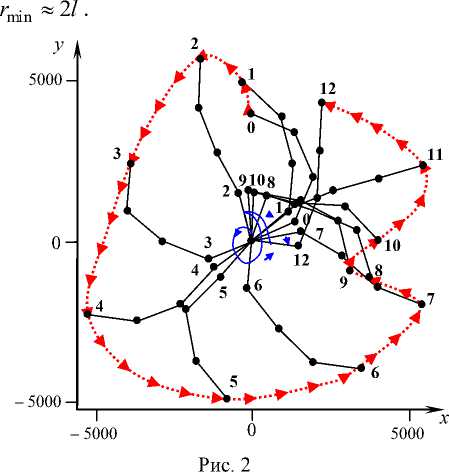
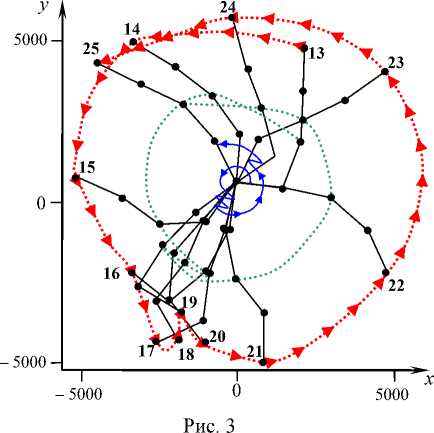
Конечное состояние БОКС при 1 12 = 5676 с на первом обороте (рис. 2) соответствует начальном t ₁₃ на втором обороте (рис. 3). Траектория пятой точки на втором обороте при t e [ t 13 , 1 ₂₅ ] , 1 ₂₅ = 2 t 13 является замкнутой, с "перекрытием" полярного угла пятой точки Av 5 ~ 0,4 п , v 5 = 2 n + Av 5 .

На траектории пятой точки от момента 116 = 7095 с до момента 121 = 9460 с происходит смена знака касательного ускорения: от убывания при t e[t16, t18 ] к возрастанию при d^ s  л t е^8, t2 J,   при этом ---5 < 0 при dt t е [t18, t19] •

Траектория средней точки m ₃ цепочки на рис. 3 отмечена зелеными точечками. Угол «перекрытия» на этой траектории, определяемый конечным и начальным положением точки m 3 , А^ з « 0,5 п , ^ з = 2 п + А^ з . Обратное движение точки m ₃ определяется условием d ^ ---— < 0 и происходит при t е [6₇, 6 ₉].

dt                                ⁷

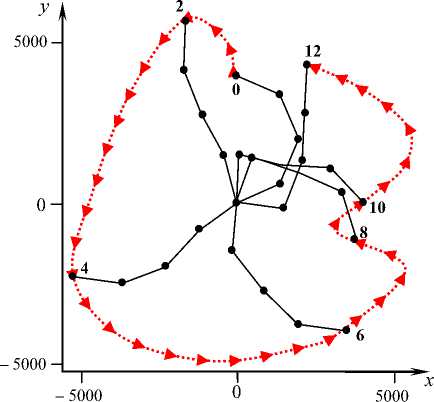
Рис. 4

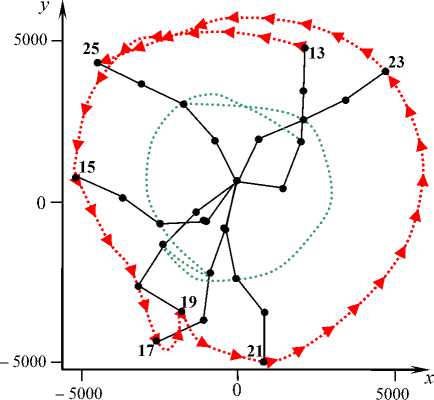
Рис. 5

Картина движения БОКС, представленная на рис. 2, 3 с шагом A t = 473 с, повторена на рис. 4, 5 с шагом A t = 946 с. При этом более отчетливо отслеживается динамика изменения формы цепочки стержневой пятиточечной БОКС.

Заключение

Математическая модель БОКС цепочечной структуры, описанная в данной работе, может быть использована для дальнейшего анализа больших космических систем.

Исследование движения 5-массовой системы проводилось численно с применением пакета Mathematica в предположении равных длин стержней, равных масс точек, мгновеннопоступательного начального состояния системы в плоском центральном гравитационном поле. Приведено описание последовательных состояний системы в транспортирующей системе координат на промежутке двух оборотов системы вокруг опорной точки.

Создана визуализация движения 5-массовой системы.