Свойства интегрируемости NC10-многообразий

DOI:

В данной работе мы продолжаем изучение геометрии NC ₁₀-многообразий, начатое в работах [3–5]. Интерес к этому классу многообразий вызван тем фактом, что этот класс многообразий обобщает хорошо изученный класс косимплектических многообразий. Более того, они обобщают класс точнейше косимплектических многообразий. В данной статье мы исследуем свойства интегрируемости данной структуры, что составляет основную цель статьи.

Пусть М – гладкое почти контактное метрическое многообразие (коротко, AC -многообразие), размерности 2 n + 1, X ( M ) - C “ -модуль гладких векторных полей на многообразии М. В дальнейшем все многообразия, тензорные поля и т. п. объекты предполагаются гладкими класса C “ .

Определение 1 [3]. AC -структура, характеризуемая тождеством

V x ( ф ) Y + V y ( Ф ) X = ^ V x ( п ) Ф Y +

+ ^ V _Y ( п ) Ф X + n ( X К _Y ^ + n ( Y К X£ X , Y е X ( M ),

называется NC ₁₀ -структурой . AC -многообразие, снабженное NC ₁₀-структурой, называется NC ₁₀- многообразием .

Полная группа структурных уравнений NC ₁₀-структуры на пространстве присоединенной G -структуры имеет вид [3]:

• 1)    d ю = F ab ю a л ю ^b + F ab to a л ю _b ;

• 2)    d ю a = - 0 a л ю ^b + C a ю_b л ю _c + F a ю _b л ю ;

• ³⁾    d ^ю a = ⁰ a ^{л ю} b ⁺ C abc ^ю b ^{л ю} c ⁺ F ab ^ю b ^{л ю} ;

  
  

• 4)    d 0 b + 0 a л 0 b = ( A ad - 2 C ad^b C hbc - F ad F bc ) ю ^c л ю _d ,

  где

  
  

  С abc

  

  —

  
  
  
  

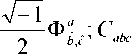
• ¹    fTi a ■ /^babc ]    abcbc , ^л __         , ababc   ^л ,

• ^{— ф} b , c ; ^C     = C ; C [ abc ] = C abc ; ^C = C abc ;

F“^b = 7— 1 Ф 0 ,; F_ah = — Т ^ 1ф 0 ₆; F^ab + F^ba = 0; F_ah + F_ha = 0; _{a ˆ} b    ab                a,b                             ab ba

j ^ad _ j^{[ a}d ^] _ TT dbcbc _ Tdad_r _ _n A bc ]    A bc     °; ^Fad^{C F} C dbc ° ^.

Тождество F^adC_dbc = 0 называется первым фундаментальным тождеством NC ₁₀-структуры; тождество A bd C ^ ] _d = 2 C^adhC_hb [ _cC gf ] _d - вторым фундаментальным тождеством ; тождество A bdc F dg ] = F^adF_b [ c F d g ] - третьим фундаментальным тождеством [4; 5].

Предложение 1 [3]. NC ₁₀-структура является: 1) точнейше косимплектической тогда и только тогда, когда второй структурный тензор равен нулю, то есть F = 0; 2) структурой класса C ₁₀ тогда и только тогда, когда первый структурный тензор равен нулю, то есть C^abc = C_abc = 0; 3) косимплектической структурой тогда и только тогда, когда C^abc = C_abc = 0, F^ab = F_ab = 0.

Поскольку to = to⁰ = n * ( n ) , где п - естественная проекция пространства присоединенной G -структуры на многообразие М , то из (2:1) следует, что контактная форма NC ₁₀-структуры замкнута тогда и только тогда, когда F^ab = F_ab = 0, то есть когда, согласно Предложения 1, NC ₁₀-структура является точнейше косимплектической. Так как всякое точнейшее косимп-лектическое многообразие локально эквивалентно произведению приближенно келерова многообразия на вещественную прямую [2], то доказана следующая теорема.

Теорема 1. NC ₁₀-многообразие имеет замкнутую контактную форму тогда и только тогда, когда она является точнейше косимплектическим многообразием, то есть когда локально эквивалентно произведению приближенно келерова многообразия на вещественную прямую. Если многообразие односвязно, то указанные локальные эквивалентности можно выбрать глобальными.

Напомним [2], что компоненты тензора Нейенхейса

N ф (X, Y) = 1 {ф2 [X, Y ] + [фX, ф Y ] — ф[фX, Y ] — ф[X, ф Y ]} на пространстве присоединенной G-структуры имеют следующий вид:

Определение 2 [2]. Почти контактная метрическая структура называется интегрируемой, если N = 0.

Теорема 2. Интегрируемая NC ₁₀-структура является косимплектической структурой.

Доказательство. Пусть NC ₁₀-структура является интегрируемой, тогда из определения 2 и (4) следует, что F ab = F a = 0, C^abc = C_abc = 0. Тогда, согласно Предложения 1, NC ₁₀-структура является косимплектической структурой. ^

Поскольку всякое косимплектическое многообразие локально эквивалентно произведению келерова многообразия на вещественную прямую [2], то предыдущую теорему можно сформулировать в следующем виде.

Теорема 3. Интегрируемая NC ₁₀-структура локально эквивалентно произведению келеро-ва многообразия на вещественную прямую. Если многообразие односвязно, то указанные локальные эквивалентности можно выбрать глобальными.

Известно [5], что задание тензора Нейенхейса равносильно заданию четырех тензоров N ⁽¹⁾, N ⁽²⁾, N ⁽³⁾, N ⁽⁴⁾, а именно:

N ^{( 1 )} ( X , Y ) = N ( X , Y ) + 2 d n ( X , Y £; N ^{( 2 )} ( X , Y ) = ( L _{ф х} п X Y ) - ( L ф y n )( X ) ;

N ^{( 3 )}( X ) = ( L , ФХ X ); N ^{( 4 )}( X ) = ( L ^( X ); X , Y g X ( M ) ,                   (5)

где L_X – производная Ли в направлении векторного поля X .

Вычислим компоненты этих тензоров на пространстве присоединенной G -структуры.

Учитывая, что ю = ю⁰ = п * ( п ) , где п - естественная проекция пространства присоединенной G -структуры на многообразие М , а также то обстоятельство, что на пространстве присоединенной G -структуры ^ a = ^ a = 0, с⁰ = 1 , согласно (2:1) находим, что на этом пространстве:

• 1)    ( d п 8 ^ ) aa = ( d n 8 ^ ) aa = 0; 2) ( d n 8 ^ t = F_ab ; 3) ( d n 8 ^ ) 0 ь = F^ab ;

• 4)    ( d n 8 $ _b = ( d n 8 ^ = 0; 5) ( d П 8 ^ ) 0 . = ( d n 8 $ 0 = 0;                          (6)

• 6)    ( d n 8 ^ ) 0 a = ( d n 8 ^ ) 00 = 0; 7) ( d n 8 ^ ) 00 = 0.

С учетом соотношений (4) и (6) получим, что на пространстве присоединенной G -структуры тензор N ^{( 1 )} ( X , Y ) = N ( X , Y ) + 2 d n ( X , Y ) ^ имеет следующие компоненты:

Из теорем 2–4 имеем следующую теорему.

Теорема 5. Пусть 5 = ( ^,n, Ф , g = (у}) — AC -структура. Тогда следующие утверждения эквивалентны:

• 1)    5 = ( ^,п, Ф , g = (у)) — интегрируемая NC 10 - структура;

• 2)    5 = ( ^,п, Ф , g = (•,•) ) — нормальная NC ₁₀-структура;

• 3)    5 = ( ^,n, Ф , g = (у}) — косимплектическая структура.

Теперь вычислим компоненты тензора N ^{( 2 )} ( X , Y ) = ( L _Ф X n )( Y ) — ( L _Ф Y n )( X ) , где L X — производная Ли в направлении векторного поля X .

Определение 4 [2]. Пусть М - гладкое многообразие; Х - векторное поле на М ; { F t } -соответствующая ему локальная однопараметрическая группа диффеоморфизмов многообразия; Т - тензорное поле типа ( r , 5 ) на М . Производной Ли тензорного поля Т в направлении векторного поля Х называется тензорное поле L X T на М , в каждой точке p е M определяемое формулой

• ⁽ L X T ) - = Й; (⁽ F - ■ ) * ^T« - ) — ^T- > •                               (8)

Оператор L _x : T ( M ) ^ T ( M ) , сопоставляющий тензорному полю T е T ( M ) тензорное поле L X T , называется оператором дифференцирования Ли в направлении векторного поля Х .

Оператор дифференцирования Ли обладает следующими свойствами [2]:

• 1)    оператор L_X является дифференцированием тензорной алгебры T ( M ) многообразия, сохраняющим тип тензоров и перестановочным с операторами свертки;

• 2)    L x f = X ( f ) , V f е C “ ( M ) ;

• 3)    L X Y = [ X , Y ], X , Y е X ( M ) .

Замечательным обстоятельством является то, что перечисленные свойства оператора дифференцирования Ли однозначно определяют этот оператор.

Замечание [2]. Пусть t - произвольный тензор типа ( r , 5 ) на М . Выражение L _x ( t ) ( X 1 ,..., X_r , u ¹ ,..., u⁵ ) , будучи линейным по аргументам X 1 ,..., X_r , u 1 ,..., u⁵ , не является линейным по аргументу Х .

С учетом перечисленных свойств имеем:

L ф X ( n ( Y )) = L ф X ( с Д ® Y ) = C$ L ф X ( n ® Y ) = C$L ф x ( n ) ® Y + C Д ® L ф x ( Y ) = L ф x ( n ) ® Y + n ® L ф x ( Y ) , ^{то ест}ь L ф x ( n ( Y )) = L ф x ( n ) ® ^{Y +} П ® L Ф X ( ^{Y ) .}

С учетом тождества [ X , Y ] = V _X Y - V Y X и свойств оператора дифференцирования Ли, из полученного равенства имеем:

L ф X ( n )( Y ) = L ф X ( n ( Y )) - n ( L ф x Y ) = ( ф X )( n ( Y )) - п ( [ Ф X , Y ] ) =

= ( Ф X )( n ( Y )) - n ( V ф x Y ) + n ( V Y ( Ф X )) = {( Ф X )( n ( Y )) - n ( V ф x Y )} +

+ n { V Y ( Ф ) X + ФV Y X } =V ф x ( n )( Y ) + n { V Y ( Ф ) X } + n { ФV Y X } =

= VфX (n)(Y) + n{V Y (ф)X}, то есть

L ф X ( n )( Y ) = V ф X ( n )( Y ) + n { V Y ( Ф ) X } ; V X , Y е X ( M ) .                     (9)

Рассмотрим характеристический вектор NC 10 -многообразия. Поскольку ^ является тензором типа (0,1), то его компоненты { ^ i } на главном расслоении B ( M) реперов над М удовлетворяют дифференциальным уравнениям [2]:

d^ i - ^ k 0 k = ^ i^j,                                         (10)

где { ^ 'j } - система функций, служащая компонентами ковариантного дифференциала вектора ^ в связности V . Расписывая (10) на пространстве присоединенной G -структуры, с учетом соотношений ^ a = ^“ = 0, £ ° = 1 и вида тензорных компонент формы римановой связности [3]:

1) 0 a = C^abc ы c ; 2) 0" = C _abc ы c ; 3) 0_o a =- F^ab ы „ ; 4) 0 0 =- F _ab ы ^b ;

• 5) 0 a = F ab ы b ; 6) 0 0 = F^ab ы b ; 7) 0 0 = 0; 8) 0 j + 0 j = 0,

получим:

1) ^ = -F; 2) ^ =-Fab, а остальные компоненты нулевые.

Теорема 6. Характеристический вектор £ NC ^-структуры является вектором Киллинга.

Доказательство . Поскольку F^ab + F^ba = 0, F_ab + F_ba = 0, то ^ i , j + ^ j , i = 0 , то есть VV X ^, У ) + ( X , V _у^ = 0, V X , У е X ( M ) , то есть ^ - вектор Киллинга. □

Аналогично для контактной формы n NC ^-многообразия:

1)П a , b =- F ab ; 2)n a , b =- F^ab ,                                   (13)

а остальные компоненты нулевые.

Теорема 7. Контактная форма n NC ₁₀-структуры является формой Киллинга.

Согласно соотношению (9), имеем:

N ^{( 2 )}( X , У ) = L _ф x №) - L ф у ( n )( X ) = = V ф x №) + n { V у ( Ф ) X } -V ф у ( n )( X ) - n { V x ( Ф ) У } , V X , У е X ( M ), то есть

N(2)(X,У) = Vфx№)+n{Vу (Ф)X}-Vфу (n)(X)-n{Vх(ф)У}, VX,У е X(M).

Из (14) следует, что N ^{( 2} ) ( X , У ) = - N ^{( 2} ) ( У , X ) , то есть тензор N ^{( 2 )}( X , У ) кососимметричен, то есть является 2-формой.

На пространстве присоединенной G -структуры тождество (14) примет вид:

Nj) = П j,kФk - Пi,kФk + ПkФkj - Пk Фk,i.(15)

С учетом соотношений n _a = n _a = 0, n₀ = 1 и вида матрицы Ф, из (15) имеем:

1) Nab} = 4V-1Fab; 2) Nab) = -4V-1Fab,(16)

остальные компоненты нулевые.

Из (16) непосредственно имеем следующую теорему.

Теорема 8. На NC ₁₀-многообразии N ^{( 2 )}( X , У ) = 0 тогда и только тогда, когда F^ab = F_ab = 0.

Из Предложения 1 и теоремы 8 следует теорема 9.

Теорема 9. NC 10 -многообразие с N ^{( 2} ) ( X , У ) = 0 является точнейше косимплектическим многообразием.

Используя локальное строение точнейшее косимплектического многообразия [2], теорему 9 можно сформулировать следующим образом.

Теорема 10. NC ₁₀-многообразие с N ^{( 2 )}( X , У ) = 0 локально эквивалентно произведению приближенно келерова многообразия на вещественную прямую. Если многообразие односвязно, то указанные локальные эквивалентности можно выбрать глобальными.

Рассмотрим теперь тензор

N ^{( 3 )} ( X ) = L , ( Ф )( X ) = L , ( Ф X ) - Ф L , X = [ ,, Ф X ] - Ф [ ,, X ] = = V , ( Ф X ) -У_ф X , - ф ( у , X - V X , ) = V , ( ф ) X + ФУ X , -- У ф X , - ФУ , X + ФУ X , = V ( Ф ) X - У ф X , + ФУ X ,.

Таким образом, на NC ₁₀-многообразии:

N ^{( 3 )}( X ) = V , ( Ф ) X -У ф X , + ФУ X ,, V X g X ( M ).                      (17)

На пространстве присоединенной G -структуры тождество (17) равносильно соотношениям:

• 1)    ( N ^{( 3 )} ) b = - 2V-T F a ; 2) ( N ^{( 3 )} ) a = 2V-T F_ab ,                         (18)

остальные компоненты нулевые.

Из (18) и Предложения 1 следует теорема 11.

Теорема 11. На NC ₁₀-многообразии N ^{( 3 )}( X ) = 0 тогда и только тогда, когда F ^ab = F _ab = 0, то есть когда многообразие является точнейше косимплектическим многообразием.

Используя локальное строение точнейше косимплектического многообразия [2], теорему 11 можно сформулировать следующим образом.

Теорема 12. NC ^-многообразие с N ^{( 3 )}( X ) = 0 локально эквивалентно произведению приближенно келерова многообразия на вещественную прямую. Если многообразие односвязно, то указанные локальные эквивалентности можно выбрать глобальными.

И, наконец, рассмотрим тензор N ^{( 4 )}( X ) = ( Ц n ) ( X ); V X g X ( M ) . Имеем

N(4)( X ) = (L МX ) = L, (П( X))-П(L, X )= ,(П( X))-П([,, X ]) = = V, (П( X))-П(У, X)+n(v, X )=V, (n)( X) + n(V, X )=V, (n)(X), то есть

N ^{( 4 )} ( X ) = V , ( n )( X ) ; V X g X ( M ) .                             (19)

С учетом (13), тождество (19) на пространстве присоединенной G -структуры равносильно соотношениям: ( N ^{( 4 )} ) i = 0, то есть N ^{( 4} ) ( X ) = 0. Таким образом, имеет место следующая теорема.

Теорема 13. На NC ₁₀-многообразии N ^{( 4 )}( X ) = 0.

Результаты теорем 1, 7–12 можно сформулировать в виде следующей основной теоремы.

Основная теорема. Пусть М – NC ₁₀-многообразие. Тогда следующие утверждения эквивалентны:

• 1)    NC ₁₀-многообразие имеет замкнутую контактную форму;

• 2)    F ab = F ab = 0;

• 3)    N ^{( 2 )}( X , Y ) = 0;

• 4)    N ^{( 3 )}( X ) = 0;

• 5)    М – точнейше косимплектическое многообразие;

• 6)    локально эквивалентно произведению приближенно келерова многообразия на вещественную прямую. Если многообразие односвязно, то указанные локальные эквивалентности можно выбрать глобальными.