Течение моментной анизотропной жидкости в тонких слоях
Автор: Ситникова М.А., Скульский О.И.
Журнал: Вестник Пермского университета. Серия: Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (28), 2015 года.
Бесплатный доступ
На основе анизотропной моментной гидродинамики рассмотрено течение жидкости в тонком канале. Получены аналитические выражения для профилей продольной и угловой скоростей при различных толщинах слоя. Показано, что анизотропия свойств реализуется лишь вблизи твердых поверхностей.
Моментная гидродинамика, модель анизотропной жидкости, тонкие слои, аналитические решения, продольные и угловые скорости
Короткий адрес: https://sciup.org/14729964
IDR: 14729964
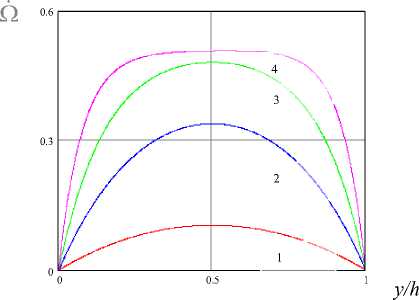
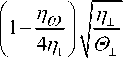
Список литературы Течение моментной анизотропной жидкости в тонких слоях
- Калугин А.Г., Механика анизотропных жидкостей. М.: МГУ, 2005. С. 64.
- Победря Б.Е. Задача в напряжениях для анизотропной среды//Прикладная математика и механика. 1994. № 1. С. 77-85.
- E.L. Aero, K.M. Bessonov and A.N. Bulygin. Dynamics of a liquid with momentum anisot-ropy//J. Appl. Maths. Mechs. 1996. V 60, №5. P. 769-775.
- Аэро, Э. Л., Вакуленко С.А. Кинетика нелинейных ориентационных деформаций в нематических жидких кристаллах в однородном магнитном поле//Прикладная математика и механика. 1997. Т. 61, вып. 3. С.479-489.
- Aero E.L., Bessonov N.M. and Buligin A.N. Normal stresses and dissipation in anisotropic liquids with oriented particles//Fluid dynamics 1997. 32, №4. P. 561-566.
- Aero E.L, Bessonov N.M., Buligin A.N. Anomalous properties of a liquid new the solid surface and moment theory//Colloid Journal, 1998 60, №4. P. 406-412.
- Аэро Э.Л., Бессонов H.M., Булыгин A.H. Динамика моментной анизотропной жидкости//Прикладная математика и механика. Т. 60. 1996. № 5. С.778-85.
- Дерягин Б.В., Алтоиз Б.А., Поповский Ю.М. и др. Влияние поверхности на образование и свойства граничных мезофаз//Докл. АН СССР. 1989. Т. 305. № 6. С. 1392-1395.
- Дерягин Б.В., Алтоиз Б.А., Никитенко И.И. Исследование структурных характеристик эпитропных ЖК-фаз некоторых органических жидкостей//Докл. АН СССР. 1988. Т.300.№ 2. С. 377-380.
- Матвеенко В.Н., Кирсанов Е. А. Ориентационная упорядоченность изотропной фазы нематогенных соединений на границе с твердым телом//Коллоидный журнал 1994. Т. 56. №2. С. 197-200.
- Голубятников А. Н. Аффинная симметрия сплошных сред//Успехи механики. 2003. Т. 2, № 1. С. 126-183.
Статья научная
