Течение нелинейной вязкопластической жидкости в плоском канале
Автор: Колодежнов Владимир Николаевич, Веретенников Александр Сергеевич
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Теоретическая механика
Статья в выпуске: 2, 2022 года.
Бесплатный доступ
Проведен анализ механического поведения концентрированных суспензий мелкодисперсных частиц, по результатам которого отмечена немонотонность зависимости вязкости таких сред от скорости сдвига. Предложена реологическая модель комбинированного типа для вязкопластических рабочих сред такого рода, которая предполагает три характерных варианта поведения на трех смежных диапазонах изменения скорости сдвига. На первом диапазоне зависимость касательного напряжения от скорости сдвига описывается линейной функцией и характеризуется постоянным значением вязкости. На втором и третьем диапазонах скорости сдвига эта зависимость аппроксимируется нелинейными функциями, описывающими, соответственно, дилатантное и псевдопластическое поведение. На основе такой модели получено решение задачи об установившемся течении рабочей среды в плоском канале. Проведен анализ влияния основных параметров рассматриваемой системы на характеристики распределения скорости.
Реологическая модель, вязкопластическая жидкость, скорость сдвига, касательное напряжение, вязкость
Короткий адрес: https://sciup.org/148325655
IDR: 148325655 | УДК: 532.135 | DOI: 10.18101/2304-5728-2022-2-71-84
Текст научной статьи Течение нелинейной вязкопластической жидкости в плоском канале
Механическое поведение большинства известных жидкостей подчиняется ньютоновской реологической модели, в соответствии с которой касательное напряжение оказывается пропорциональным скорости сдвига.
Вязкость жидкости определяется крутизной кривой течения, построенной в координатах «скорость сдвига — касательное напряжение». Естественно, что для ньютоновских жидкостей вязкость принимает постоянное значение.
Вместе с тем хорошо известны так называемые неньютоновские жидкости [1], которые, как правило, характеризуются монотонным характером изменения вязкости от скорости сдвига. В частности, для псевдопластиче-ских жидкостей вязкость монотонно снижается по мере увеличения скорости сдвига, а для дилатантных жидкостей — монотонно возрастает [2]. Для описания механического поведения таких сплошных сред привлекаются степенные законы зависимости вязкости от скорости сдвига.
Как показывают многие экспериментальные исследования, суспензии мелкодисперсных частиц твердой фазы демонстрируют еще более сложное механическое поведение, основные особенности которого проявляются, прежде всего, в немонотонном характере зависимости вязкости от скорости сдвига [3–8]. Такие жидкости, нередко, демонстрируют чередование участков возрастания и убывания вязкости на различных диапазонах изменения скорости сдвига.
Еще одна особенность поведения концентрированных суспензий мелкодисперсных частиц заключается в следующем. При приближении скорости сдвига к некоторому критическому значению крутизна кривой течения, характеризующая вязкость, начинает резко возрастать. При этом для некоторых суспензий такое возрастание вязкости становится настолько существенным (зачастую, на один-два порядка), что такую ситуацию можно интерпретировать как проявление эффекта «упрочнения» или «отвердевания». Рабочие среды такого рода получили название STF (Shear Thickening Fluids) [3].
Различные вопросы математического моделирования механического поведения нелинейно-вязких жидкостей, в том числе с помощью моделей комбинированного типа, нашли свое отражение в работах [9–14].
В [13] рассмотрен пример реологической модели жидкости, вязкость которой на разных диапазонах изменения скорости сдвига принимает различные значения. При этом полная зависимость вязкости от скорости сдвига описывается непрерывной кусочно-линейной функцией. В этой же работе рассмотрена задача о течении жидкости такого рода в плоском канале.
В данной работе предложена реологическая модель жидкости комбинированного типа с тремя участками различного поведения на отдельных диапазонах изменения скорости сдвига. Такая модель учитывает пластические свойства жидкости и предполагает учет проявления эффекта «отвердевания». На основе этой модели рассмотрено решение задачи об установившемся течении в плоском канале.
1 Реологическая модель
Кривые течения для отдельных видов суспензий мелкодисперсных частиц демонстрируют наличие трех характерных диапазонов изменения скорости сдвига, на каждом из которых реализуется свой, вполне конкретный вариант механического поведения.
На первом диапазоне при сравнительно небольших значениях модуля скорости сдвига | у | кривая течения имеет практически линейный вид, что соответствует постоянному значению вязкости ц 0. Здесь же предполагается, что касательное напряжение превышает предел текучести.
При превышении модулем скорости сдвига некоторого порогового уровня у 0 поведение кривой течения меняется и график зависимости модуля касательного напряжения |г| от | / | принимает нелинейный вид. При этом вязкость начинает возрастать подобно тому, как это имеет место для дилатантных жидкостей. Такой режим возрастания вязкости реализуется до еще одного порогового значения скорости сдвига / max > Y o, при котором вязкость достигает своего максимального значения ц тах. И, наконец, при превышении модулем скорости сдвига второго порогового уровня Y max начинается реализация очередного режима механического поведения суспензии. В этом случае функция | т (| у |)| по прежнему остается монотонно возрастающей по некоторому нелинейному закону. Однако вязкость на этом диапазоне изменения скорости сдвига монотонно снижается, что характерно для псевдопластических жидкостей.
Схематично вид кривой течения для подобных суспензий представлен на рис. 1.
Принимая во внимание возможное разбиение кривой течения на три характерных участка, зависимость касательного напряжения от скорости сдвига в области вязкого течения предлагается описывать следующей функцией
I т (1 у\ )|= <
т p + ^ o • |Y| ;
т - k 1 • ( Y i - | у |) n 1;
Т 2 + k 2 -(I У\ - У 2 ) ” 2 ;
0 ^ | у | ^ у о ;
У 0 ^ | У | ^ / max |у\ ^ / max;
где т p — напряжение сдвига, которое необходимо принять во внимание для случая, когда жидкая основа суспензии обладает пластическими свойствами; т 1 , т 2, k 1 , к 2, / 1 , / 2, n 1 , n 2 — параметры реологической модели.
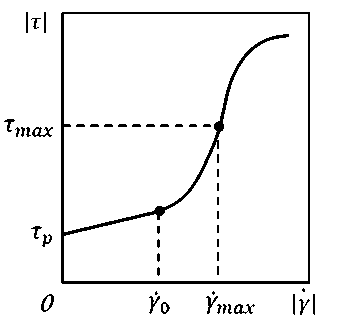
Рис. 1. Схематичный вид зависимости касательного напряжения от скорости сдвига
Вязкость жидкости будем определять посредством соотношения
a( И )=
d т d у
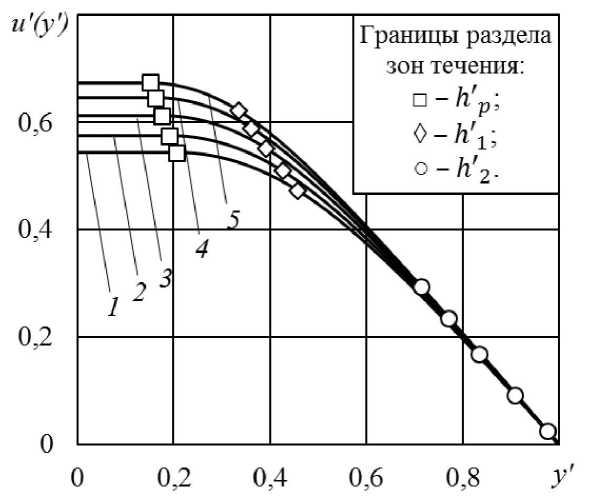
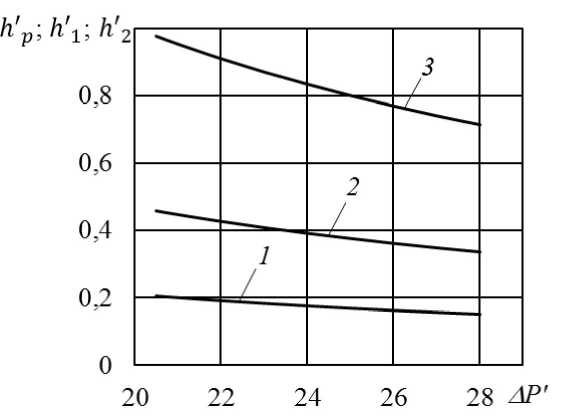
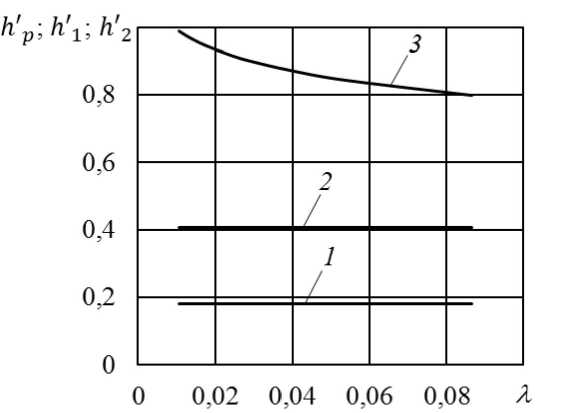
В рамках такой реологической модели предполагается, что на ее основные параметры накладываются следующие ограничения т1 >тp; Y2 При этом предполагается, что функция (1) зависимости касательного напряжения от скорости сдвига является непрерывно дифференцируемой. Требуя тогда сопряжения значений касательного напряжения (1) и вязкости (2) на границах раздела отдельных диапазонов изменения скорости сдвига, приходим к необходимости выполнения следующих соотношений Y = '• - Y.A. k = Ao (1 — n) "1-1 . k = An . Y1 11’1 \ni —1 2 An 2 —1 1 - Z ni ( Ymax-Yo ) n 2 '( Ymax-Y2 ) - А-и + Ao"(Ymax -Y0) • T = T - Ao ^n' ) T1 Tp+ A0 Y 0 + ; 12 1 max (Y max Y 2 ) . n • (1 - n n2 Здесь для краткости записи приняты обозначения n = Mmax X Mo ni-1 < 1; T max = тp + Ao • Y&o + M0 ^ Ymax — Y0 H1— ^n ) П1 ^(1 - П ) где тmax — касательное напряжение в жидкости, достигаемое при | Y\ = Y&max. Принимая во внимание последние соотношения, приходим к выводу о том, что реологическая модель (1) должна определяться следующим набором восьми независимых параметров: тp, Ao, Amax, Yo, Y&max, Y2, П1, n2. Также специально отметим, что, удовлетворяя условию непрерывной дифференцируемости для касательного напряжения, в случае зависимости вязкости от скорости сдвига выполняется лишь условие непрерывности. Иначе говоря, график зависимости вязкости от скорости сдвига, оста- ваясь непрерывным, допускает наличие «изломов» на границах раздела смежных диапазонов изменения скорости сдвига. Только что рассмотренная реологическая модель допускает учет проявления эффекта «отвердевания». В такой ситуации формально с учетом (2) должно выполняться условие lim < I Y\^ d И > = № . Принимая во внимание неравенства (3) для n1 и n2 , можно видеть, что для выполнения (4) необходимо, в свою очередь, потребовать выполнение следующего условия Y1 = Y2 = Ymax . (5) Тогда, обеспечивая с учетом (5) непрерывную дифференцируемость для функции (1), приходим к следующим соотношениям k1 = A, «1 •( Ymax - Yo )"' T = T = ття „. 1 2 max При этом параметр тmax должен определяться следующим образом • 1 1 I Мл * Ymax Tmax = Tp + Mo * Yo * 11+ 0 . I «1 ) «1 Таким образом, для случая, когда реологическая модель обеспечивает учет эффекта «отвердевания», из последних соотношений приходим к выводу о том, что реологическая модель (1) должна определяться следующим набором из семи независимых параметров: тp, ц0, Yo, Ymax, k2, ni>n2. 2 Течение нелинейной вязкопластической жидкости в плоском канале Рассмотрим одномерное, установившееся, ламинарное течение в плоском канале ширины 2 • h и длины L за счет перепада давления AP для вязкопластической жидкости, реологическая модель которой описывается соотношением (1). Введем декартову систему координат традиционным образом для задач такого рода, сориентировав продольную ось Ox вдоль оси симметрии канала, а ось Oy — по нормали к ней. Учитывая ожидаемую симметрию течения относительно оси Ox , решение задачи проведем только для у > 0. В соответствии с реологической моделью (1) в канале в зависимости от величины перепада давления могут быть реализованы несколько схем течения. В частности, если выполняется условие АР< АР0= (тp • L) / h , то течение в канале оказывается невозможным. Однако при некотором превышении перепадом давления уровня АР0 в канале формируются две зоны течения. В промежутке между стенками канала и центральной зоной пластического течения будет располагаться зона сдвигового течения с постоянным значением вязкости ц0. При этом скорость сдвига будет подчиняться условию |у| < Y0. Такая схема хорошо известна и соответствует течению вязкопластической жидкости Бингама. Дальнейшее увеличение перепада давления и превышение им некоторого значения АР >АР0 приводят к формированию в канале очередной схемы с еще одной зоной, но уже нелинейно-вязкого течения. Эта зона располагается у стенок канала. При этом внутри нее скорость сдвига удовлетворяет условию Y0< |/| < Ymax • И, наконец, завершающая схема нелинейно-вязкого течения возникает при последующем увеличении перепада давления выше некоторого уровня АР2>АР1, когда в окрестности стенок канала формируется очередная зона, внутри которой для скорости сдвига выполняется условие |y| > Ymax. Естественно, что каждой отдельной зоне течения, согласно реологической модели (1), должна соответствовать своя зависимость касательного напряжения от скорости сдвига. Рассмотрим далее случай, когда для заданного перепада давления АР > АР2 реализуется наиболее общая схема течения, представленная на рис. 2. Тогда в зависимости от диапазона изменения скорости сдвига в канале могут быть выделены четыре различные зоны течения . Рис. 2. Схема течения Центральную часть канала в полосе ширины 2 • hp будет занимать зона пластического течения с постоянным значением скорости. В диапазоне изменения поперечной координаты hp< |y'| < h будет располагаться зона течения с постоянным значением вязкости ц0. В этой зоне скорость сдвига будет принимать значения из интервала 0 < |/| < /0. В следующих двух диапазонах изменения поперечной координаты h< |y| < h2 и h2 < |y'|< h будут располагаться зоны нелинейно-вязкого течения, соответствующие следующим диапазонам изменения скорости сдвига /0< |/| < ymax и Y\ ^ Y&max. Для определенности далее будем отмечать соответствующие характеристики течения верхними индексами в круглых скобках (p), (0), (1), (2) , указывая на их принадлежность к зоне пластического течения, зоне течения с постоянным значением вязкости, а также первой и второй зонам нелинейно-вязкого течения соответственно. Здесь же отметим, что все только что введенные в рассмотрение параметры hp, h 1, h2, определяющие положение границ отдельных зон течения по поперечной координате, не известны заранее и должны определяться в ходе решения поставленной задачи. Распределение скорости u жидкости и давления P в канале должно удовлетворять следующим уравнениям динамики и условию неразрывности потока, представленным в безразмерной форме записи r dp* a G=; = 0; = 0; dx' ay' dy' dx' тxy Г(f) = <т'(1)(f) = т2 (п -т p + k0^ Y&x(0); -T’ + kx •( Y1 + Y'(1)) n1; u'(y ') = < -т2 - k2 •(—/ u,(p) = const; u,(0)(y‘); u (yx); u,(2)(y‘); - Г2) ; p '2 У У У ' p; - 2; du'(p ) yXp) = 0; Y’1) = du— < 0; dy' т X? < 0; г = 0,1,2. В последних выражениях и далее безразмерные координаты, параметры и функции отмечены верхним штрихом и определены посредством соотношений yx y = h • ; = L • p *=—; T max u' u ; vs hp = hp; h h ' = h-; 1h ’ h2 = — • h ; т' = Txy . xy T ; max Y'=; Y&max т p = тp ; T max Y0 =4 Y0 . Y ; max т' = Ti . ; T max ■ Y1 = Ymax т T 2 2 - T max if _ Mo * Ymax . k 0 = - max n1 1/ _ ,v 1 Y max . _ k1 = ; k 2 = max 72 = A; Y max k * Y X 2 max ; T max G = — • v = h • у L;vs Ya max . Запишем граничные условия задачи y*=hp; y ‘ = h; y ‘ = h 2; y ‘ = 1; т'(0)=-т p; Y'(0)= Y'(1)=-Y0; Y'(1)= y '(2)=-1; T '(2)=-AP' * G ; u,(0)= u " u,(1)= u ; (2) ; u '(2) = 0. Граничные условия для давления формулируются традиционным образом, что из (6) приводит к ожидаемому выражению для его распределения вдоль оси канала P' (x') = P0-AP' * x', (14) где P0 = P0 / тmax — давление жидкости на входе в канал; AP' = AP / тmax — перепад давления на длине канала. Интегрируя первое уравнение из (6), приходим с учетом соотношений (7), (14) и граничных условий (10), (13) для касательного напряжения к выражениям, определяющим распределения скорости сдвига в основных зонах вязкого течения Y.(0)( y.) = - G_AP ( y. - hp ) ; k0 a&'(1)( y') = -a&; + Y'(2)(y') = -Y'2 - 1 (т‘ - G * AP' * y + Cf1)) k1 k^ (G *AP' * y' - т ‘) n2 n1 где C1(1) — неизвестная пока константа интегрирования. Принимая во внимание граничные условия (11), (12) для скорости сдвига, с учетом (15) приходим к системе четырех уравнений относительно hp, h, h2 и CP1, из решения которой находим h'p = ^'^ДР [r 2 + k; ■( *: — 1)" + k2 ■ (1—Y2)"2 — k 1 • (Y1—Y0)" — k0 • y0> ]; h; = —^ [r 2 +1; •( y\ — 1) "1 + k2 • (1—1&2)"2— k 0 • (f, — yO ) "1 ]; G •ДР L -1 h; = —1— 2G •ДР' — ; C^1 = T 2—< +k 2^(1—f2)"2+ k^( Y1—1) "1. С учетом (9) после интегрирования (15) приходим к следующим выражениям для скорости жидкости в соответствующих зонах вязкого течения u,(0) (y ‘) = — G•ДР'[ y,2 k0 — h'p • y' | + C201; u '(1) ( y ‘ )= f; • y ‘— k’ • "1 G •ДР ‘(n1 + 1)L k 0 ^^t— G •ДР '• y ‘ + Cf) "1 +1 n1 + C211; U,(21(y') = f0 • (1 — y') + —k^г x (Л) 2 ( Л)G•ДР'•(n2+1) x< kr( G •ДР'-т 2) 12 +1 n2 — kr( G •ДР '• y'-т 2) г 2 + n2 , где C2(0) и C2(1) — константы интегрирования. Здесь при выводе выражения (18) было использовано граничное условие (14) для скорости. Оставшиеся пока неизвестными константы интегрирования C2(0) и C2(1) находятся с привлечением граничных условий (12), (13) сопряжения ско- ростей на границах раздела соответствующих зон течения (16)–(18) принимают вид: и с учетом С? = yOh 2 + Y ;-(1 — h0) + + k’ • "1 G •ДР '•( n1 +1) L k ~(< — G •ДР •h h 2 + C) "1 +1 n1 k 2 • n2 + G •ДР' •( n2+1) • < kr( G •Д Р'-т 2) c20)= G•ДР*[ h k0 n2 — kT•(G ДР'• h2— т2) h„ • h. — 2 p J f • h1'— г 2 + n2 ; - к’ • n1 G •AP ‘(n + 1)L к ‘ U<-g •a p '• h ■с?1)) n, +1 n + C Скорость жидкости в центральной зоне пластического течения с учетом (16) принимает следующее значение u,(p) = u,(0) (hp ) = const. (19) Только что рассмотренная схема течения может быть реализована в случае, когда при AP' = AP выполняется условие h2 (AP2') = 1. Из этого условия приходим к выражению для определения порогового значения перепада давления AP‘ = Т 2 + к2^(1 - Y2) n21, G выше уровня которого распределение скорости в канале структурно определяется соотношением (8) с учетом (16)-(19). 3 Анализ влияния исходных параметров задачи на характеристики течения С привлечением полученных выше соотношений был проведен анализ влияния исходных параметров задачи на характеристики течения. В качестве примера на рис. 3 представлены распределения скорости жидкости в поперечном сечении канала для различных значений перепада давления, построенные с учетом (16)-(19) для следующего набора безразмерных параметров задачи: P0 = 4,144; AP1= 9,323; AP' = 20; G = 0,05; т p = 0,207; < = 1,866; т2 = -7,748; Y0 = 0,563; Y‘ = 1,019; Y2 = 0,5; к0 = 0,46; к’ = 1,575; к2 = 11,543; Л = 0,0407; n1= 0,15; n2= 0,4. По своей величине выбранные здесь безразмерные параметры реологической модели были близки к соответствующим значениям параметров суспензии на основе полиэтиленгликоля для частиц карбоната кальция при их объемной концентрации ф = 0,28 [3]. При этом частицы твердой фазы имели вытянутую форму и характеризовались следующими геометрическими параметрами: продольный размер — 1323±667 нм; поперечный размер — 201±73 нм. На рисунке 3 для каждого графика распределения скорости указаны положения границ раздела основных зон течения. Рис. 3. Распределение скорости течения жидкости от координаты y′ , 1 – ΔP′=20,5; 2 – ΔP′=22; 3 – ΔP′=24; 4 – ΔP′=26; 5 – ΔP′ =28 Зависимость от перепада давления положения внутри канала этих границ раздела отдельных зон течения с различным характером механического поведения для указанных выше значений исходных параметров представлена на рис. 4. Рис. 4. Зависимость границ раздела зон течения от перепада давления ΔP′ , 1 – h′p; 2 – h1′; 3 – h2′ Как и следовало ожидать, по мере увеличения перепада давления на длине канала ширина 2 ⋅ h′p центральной зоны пластического течения монотонно убывает. Монотонное убывание с ростом перепада давления демонстрируют также функции h1′(ΔP′) и h2′(ΔP′). При этом убыванию h2′(ΔP′) соответствует, естественно, расширение примыкающей к стенкам канала зоны псевдопластического течения, внутри которой (h2 < |у‘ < 1) выполняется условие |у,(2)(у')| > 1. Влияние соотношения ^max / ^0 между характерными значениями вязкости жидкости, определяемое посредством X, при прочих равных параметрах модели иллюстрируют зависимости, представленные на рис. 5. Рис. 5. Зависимость границ раздела зон течения от параметра X при \Р‘ = 23,02, 1 - hр; 2 - h ; 3 - h2 Для рассматриваемого наиболее общего случая, когда в канале реализуются четыре зоны течения, параметр X не оказывает при прочих равных параметрах влияния на изменение h' и h‘. Что же касается границы раздела между зонами дилатантного и псевдопластического поведения, то возрастание параметра X , что соответствует снижению величины соотношения вязкостей ^max / ц0, приводит к уменьшению значения h2. Заключение Проведен краткий анализ особенностей механического поведения суспензий мелкодисперсных частиц. Эти особенности предполагают немонотонное изменение касательного напряжения от скорости сдвига. Предложенная реологическая модель комбинированного типа позволяет описывать на различных диапазонах изменения скорости сдвига три различных варианта поведения: течение с постоянным значением вязкости, а также дилатантное и псевдопластическое поведение. Такая реологическая модель предполагает в том числе и возможность учета проявления эффекта «отвердевания» рабочей среды, который заключается в резком возрастании вязкости при приближении скорости сдвига к некоторому критическому значению скорости сдвига. На примере решения задачи об установившемся течении в плоском канале показано, что в наиболее общем случае область течения должна быть разделена на четыре зоны, в которых реализуются различные варинты поведения, заложенного в реологической модели. При этом наряду с зоной пластического течения следует рассматривать смежную с ней зону течения жидкости Бингама с постоянным значением вязкости, а также еще две зоны нелинейно-вязкого, соответственно, дилатантного и псевдопластического поведения. Такая методика разбиения исходной области течения на отдельные зоны с различным характером реологического поведения может быть рекомендована для решения и других задач механики жидкости.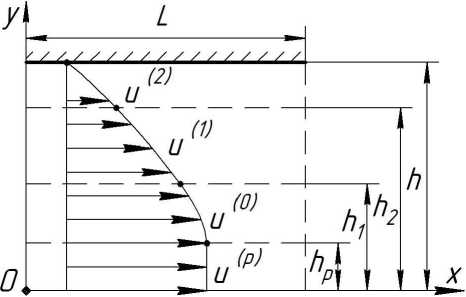
Список литературы Течение нелинейной вязкопластической жидкости в плоском канале
- Астарита Дж., Марруччи Дж Основы гидромеханики неньютоновских жидкостей: перевод с английского. Москва: Мир, 1978. 311 с. Текст: непосредственный.
- Литвинов В. Г. Движение нелинейно вязкой жидкости. Москва: Наука, 1982. 376 с. Текст: непосредственный.
- The Effect of Rheological Parameters on the Ballistic Propeties of Shear Thickening Fluid (STF) - Kevlar Composites / E. D. Wetzel, Y. S. Lee, R. G. Egres [et al.] // AIP Conference Proceeding. 2004. V. 712. P. 288-293.
- Egres R.G., Wagner N.J. The rheology and microstructure of acicular precipated calcium carbonate colloidal suspensions through the shear thickening transition // Journal of Rheology. 2005. V. 49. Iss. 3. P. 719-746.
- Extensional rheology of shear-thickening cornstarch and water suspension / E. Erica, B. White, M. Chellamuthu, J. P. Rothstein // Rheologica Acta. 2010. V. 49. Iss. 2. P. 119-129.
- Preparation of SiO2/PEG Shear Thickening System by Centrifugal Dispersion / Biao Yang, Sheng Wang, Guozhi Xu, Fei Xin // Advanced Materials Research. 2012. V. 560-561. P. 586-590.
- Brown E., Jaeger H.M. The role of dilation and confining stress in shear thickening of dense suspensions // Journal of Rheology. 2012. V. 56. P. 875-923.
- A constitutive model for simple shear of dens frictional suspensions / A. Singh, R. Mari, M. M. Denn, J. F. Morris // J. Rheol., 2018. V. 62. P. 457-468.
- Анистратенко В. А., Кошевая В. Н., Валовой Б. Н. Исследование реологических свойств фильтрационного осадка как объекта транспортирования // Известия вузов. Пищевая технология. 1992. № 1. С. 54-57. Текст: непосредственный.
- Galindo-Rosales F. J., Rubio-Hernandez F. J. Numerical simulation in steady flow of non-Newtonian fluids in pipes with circular cross-section // Numerical Simulations - Examples and Applications in Computational Fluid Dynamics. 2010. P. 3-23.
- Galindo-Rosales F. J., Rubio-Hernandez F. J., Sevilla A. An apparent viscosity function for shear thickening fluids // Journal of Non-Newtonian Fluid Mechanics. 2011. V. 166 (5). P. 321-325.
- Колодежнов В. Н. Моделирование вращательного течения между коаксиальными цилиндрами для жидкости с эффектом отвердевания // Известия РАН. Механика жидкости и газа. 2014. № 3. С. 3-14. Текст: непосредственный.
- Vazquez-Quesada A., Wagner N. J., Ellero M. Planar channel flow of a discontinuous shear-thickening model fluid: Theory and simulation // Physics of Fluids. 2017. V. 29. P. 103104.
- Скульский О. И. Реометрические течения концентрированных суспензий твердых частиц // Вычислительная механика сплошных сред. 2020. Т. 13, № 3. С. 269-278. Текст: непосредственный.


