Течение Пуазейля для жидкости с переменной вязкостью

1. Уравнения движения.

Уравнения движения вязкой жидкости в инвариантном виде (т. е. независимо от выбора системы координат) записываются следующим образом [1]

^p + div ^{( pv} ) = О,

д(pv)

I д t

+ div (pv ®v) = pF + divT,

где p и и - соответственно плотность и скорость жидкости, F - плотность массовых сил (далее полагаем F = 0), T - тензор напряжений (запись v ® v обозначает тензорное произведение).

Тензор напряжений выражается следующим образом:

T = (-p + H divu) G + 2^e,

где p - давление, H - динамический коэффициент вязкости, H — 2-й коэффициент вязкости,

G – метрический тензор (определяемый системой координат), e – тензор скоростей деформаций, который определяется как

e = 1 (Vv + (Vv)T),                                     (3)

где V - оператор набла, а символ T обозначает транспонирование.

Несложно показать, что в цилиндрических координатах ( r , ф , z ) для ковариантных компо-

нент имеют место следующие соотношения:

\ 1 d z , д I v(p | Эх X div(v) = - Ч"(rvr ) + 7--I + ?Jrvz )

r у д r         дфу r J д z

div(pv) =1J |-(rpvr ) + ^-(PVV rудr         дфУr

д / x

+ ( rPvz ) дz

(div(pv®v)) = div(pviv) =1 —(rpvivr) + — P i v i                rудr            дфУ r

+ 4-( rpvv) дz

i e { r ,V, z}

v = 1 (дvr дvV ^ - vV дr ’ rv 2 у дф дr J r ’ дVv evv   дф   rvr,

1 Iдvr д^ ^

- + — z I, 2 У д z    д r J

e V z

11 дvv +v ]

2 У дz   дф J

e zz

дv _z

. д z

Хайрисламов К.З.                                            Течение Пуазейля для жидкости с переменной вязкостью divT = -Vp + V( X divv) + 2 div (re),(8)

где компоненты div ( r e ) равны:

⁽ div ⁽ u e ) ) _r = r V ^ 7 ⁽ r ^ e rr ⁾⁺d p [ V e p r )⁺ a z ⁽ r ^ e zr ) J^- ?" e p

“(div(ue )p=-V—(r^erp)+—VT-e^ ^+—(r^ezp) ^j,

⁽ div ⁽ ^^ z = 7 (I⁽ r ^ e ^ ^{) +} ^ ' - ) ^⁽^ ))

Для случая осевой симметрии, т. е. когда — = 0, и = 0, формулы (4)-(9) упрощаются и dp принимают вид:

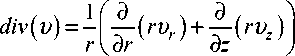
div ( ри ) = ¹ 1 |-( r pu ) + |( r pu z ) | ; r V о r          d z         J

^v ® и )), = ¹ 1 тЧ r PUU ) + |-( r PUU z ) I , i ^G { r , z } ;

1 r V dr            dz          J dU n 1 (ди du 3

rrz err          , erp , erz I +        I, d r                     2 V dz d r J epp = rUr ,         epz = 0,

ezz

duz , dz ’

( ^div ( r e ) )_r = ^{1 (} |-( ^r V ^err ) ⁺ y-( r v e zr ) ^r r V d r             d z

^^^^s

-—f> .

3 e pp , r

( ^div ( r e ) )_z = ^{1 (} |“( r V e rz )⁺ ^ ( r V e zz ) ^z r V d r            d z

2. Течение Пуазейля

Предположим, что в цилиндрической системе координат (r,p,z) течение вязкой несжимае- мой жидкости плотности р0 записывается в виде

U p = U = 0, U z = u ( r ) , 0 <  r <  R ,

причем u ( R ) = 0 , а течение стационарно. Т. е. рассматривается установившееся течение жидкости в прямой цилиндрической трубе радиуса R с условием прилипания на стенке.

Условие несжимаемости означает, что div ( и ) = 0. Тогда тензор скоростей деформаций e согласно (12) определяется следующим образом:

1 Э и er. = e„ =--, rz zr 2 dr остальные компоненты равны нулю.

Далее предположим, что динамическая вязкость v есть функция тензора e , т. е. V = А (П e ) ’

1 ( ³ и 3 2

где IIe =- I — I - 2-й главный инвариант тензора e [1, 2J, а жидкость подчиняется степенно-4 V д r J му закону, а именно справедливо соотношение n-1

V = V 0 ( - 4 Я ²Н e ) ²

( Э U

= V 0

V д r

n - 1

.2 3 V

,

Краткие сообщени^

где Д ), Л , n - постоянные, n >  1 (дилатантная жидкость [3]).

Для записи уравнений движения несжимаемой жидкости в безразмерном виде отнесем величины r и z к R , скорость к средней скорости в трубе V , плотность к р ₀, время к R / V , вязкость к д ₀ , давление к P , а компоненты тензора скоростей деформаций к P / д ₀ , где P = д ₀ V/R . Тогда второе уравнение в (1) принимает вид

Re | — + div (и ®v) | = -Vp + div (2де),                         (17)

I d t               J где Re = P0^ - параметр, называемый числом Рейнольдса. Выражение в скобках в левой части Д уравнения (17) обнуляется согласно формулам (10)-(11) и принятым допущениям о стационарности течения и несжимаемости среды. Правая часть (17) преобразуется с помощью формул

(12-14), ив безразмерном виде течение Пуазейля описывается соотношениями Э p _ д т

Э r Э z ’

Эp = 1 д( гт) Э z r д r ’ где u = u (r), 0 < r < 1, u (1) = 0, т = Д—, Э r

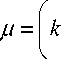
Э и

Э r

n - 1

k = 4 V .

R

Решением последних уравнений является функция

u (r ) =

n sign ( P z ) Г k\P z\ ] n k ( n + 1 ) ^ 2 _J

Г n + 1 r n

у

- 1

где p_z = Д p/L , Д p - разность давлений на концах рассматриваемого участка трубы длины L , а давление p есть линейная функция координаты z .

Подстановка в (20) n

= 1 дает известный профиль Пуазейля и ( r ) =

p z -( r ² - > )

для жидкости с

постоянной вязкостью.

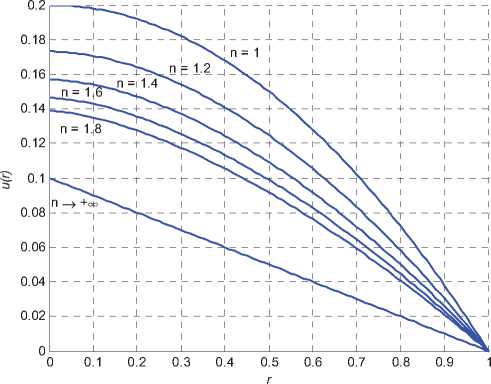
График скорости и ( r ) при различных значениях n ( к = 10 , p z =- 0,8 )

На рисунке показаны графики скорости и ( r ) в зависимости от значения n , включая , , sign ( p „), n ^ +“ - в этом случае, как следует из (20), и ( r ) =-------- ( r - 1 ) .

k

Поток, численно равный объему жидкости, протекающему через сечение трубы в единицу времени, определяется как

Хайрисламов К.З.

Течение Пуазейля для жидкости с переменной вязкостью

R

Q = 2пJ ru (r) dr,

ᴎᴫᴎ

R

Q = nJo u (r)dr .

Проинтегрировав по частям и воспользовавшись условием u ( R ) = 0 , получим

R 2 d u

Q = - n i r —dr .

* Jo д r

Переходя в (20) обратно к размерным величинам, получим du = sign (Pz) ( ^ Pz|r ^ n

• d r     Л [ 2^ J ,

  откуда

  
  

n n R ³ sign ( p_z ) ( 2| Pz\R 'J ⁿ 3 n + 1     Л ^ 2 u ₀

nR ⁴ P z 8 ^ 0

Для жидкости с постоянной вязкостью ( n = 1) получаем закон Пуазейля Q = -