Температурное нагружение составной конструкции в условиях плоской задачи
Автор: Пестренин В.М., Пестренина И.В., Ландик Л.В., Степина Е.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (22), 2013 года.
Бесплатный доступ
В условиях плоской задачи изучаются температурные напряжения в окрестности особой точки составной конструкции. Показывается, что все параметры напряженного состояния в малой окрестности особой точки претерпевают значительные изменения. Формулируется условие для материальных параметров скрепляемых элементов, обусловливающее неограниченный рост нормальных напряжений на контактной поверхности.
Концентрация напряжений, особые точки, составные конструкции, контактные поверхности
Короткий адрес: https://sciup.org/14729869
IDR: 14729869 | УДК: 539.3
Текст научной статьи Температурное нагружение составной конструкции в условиях плоской задачи
В составных конструкциях, например слоистых средах, в окрестности свободной от нагрузок границы при температурном нагружении могут возникать значительные нормальные и касательные напряжения. Такие напряжения обусловливают расслаивание конструкции, сокращают срок ее службы. Температурные напряжения в составных конструкциях изучались многими авторами. В работах [1–3] проведены экспериментальные исследования – методом фотоупругости подтверждается явление значительной концентрации напряжений вблизи края поверхности соединения составных конструкций при однородном температурном нагружении, обнаруживается влияние на максимальные значения напряжений формы линии соединения и формы образующей граничного контура. Аналитические исследования температурных напряжений в составных конструкциях рассматриваются в работах [4–10]. В статьях [4– 6] изучается напряженное состояние в области края составной конструкции, обусловленное однородными и стационарными темпера-
турными полями. Решение строится в бесконечных рядах с использованием функции Эри. В публикации [7] рассматриваемое явление изучается методами функции комплексного переменного. В работе [8] напряжения вблизи особой точки, обусловленные механическим и температурным нагружением составной конструкции, изучаются с использованием разложений, содержащих как регулярные, так и сингулярные слагаемые. В публикации [9] для изучения температурных напряжений вблизи стыка составных стержней, труб и других конструкций используются интегралы Фурье. Полученные решения ограничиваются случаем, когда скрепляемые материалы отличаются лишь коэффициентами теплового расширения. В работе [10] для анализа напряжений вблизи кромки соединяемых тел применяется вариационный подход, приводящий путем минимизации дополнительной энергии к системе обыкновенных дифференциальных уравнений.
Численные исследования, основанные на применении стандартных прикладных пакетов программ конечно-элементного анализа для изучения концентрации напряжений вблизи особых точек, оказываются неэффективными. В работе [11] показано, что полученные на основе таких пакетов решения не- адекватно отражают напряженное состояние в областях, где оно претерпевает значительные градиенты. Авторы предлагают способ улучшения МКЭ-подхода посредством введения в расчет специальных гибрид-элементов.
В настоящей работе изучение температурных напряжений вблизи свободной кромки составной конструкции проводится численно-аналитическим итерационным методом [12], позволяющим обеспечить приемлемое выполнение вблизи особой точки граничных условий и условий сопряжения на контактной поверхности соединяемых тел.
1. Постановка задачи
В декартовой ортонормированной системе координат x , x рассматривается прямоугольная пластинка, полученная соединением встык по прямой линии, принятой за ось x , двух элементов 1, 2 (рис. 1).
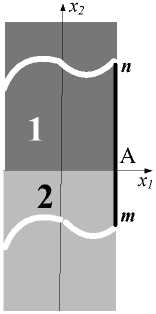
Рис. 1. Составная пластинка
вблизи точки А .
-
1) На линии контура m-n (кроме особой точки)
(1) (1) (2)(2)
^11 , и12 , ^11 ,
-
2) на линии соединения элементов
(кроме особой точки)
-
а) условия непрерывности напряжений (1) (2) (1)(2)
-
б) условия непрерывности деформаций
e^ = e(2);(3)
-
3) в особой точке
-
(1) (2) (1)(2)
& 22 & 22 = 0, & 12 = 0, & 12 = 0,
~& (г) - ~ & 22) - ( а - а ) a t = о. (5)
22 22 12
EE
Равенство (5) – условие непрерывности деформаций (3) в особой точке.
При решении поставленной задачи с использованием стандартных инженерных вычислительных комплексов (например, AN-SYS) оказывается неудовлетворительной точность выполнения приведенных выше равенств. Это объясняется прежде всего тем, что в конечно-элементных алгоритмах комплексов обычно заложено приближенное выполнение граничных условий в напряжениях. В то же время граничные условия в перемещениях выполняются точно. Это обстоятельство используется в настоящей статье, где ставится задача построения решения, с приемлемой точностью удовлетворяющего всем условиям, выраженным равенствами (1)–(5).
2. Метод решения
На каждом шаге итерационного процесса конечно-элементное решение термоупругой задачи строится с использованием разрешающих уравнений, полученных из условия стационарности смешанного функционала, в котором независимому варьированию подвергаются перемещения и деформации [13]:
J u e = J ( Lu ) TD ( e - e о )
V -
—
£ D e
dV + W . (6)
Здесь L – матрица дифференциальных операторов, с помощью которой вектор деформаций £ выражается через вектор перемещений u , D – матрица упругих модулей материала, £ 0 - вектор температурных деформаций, W – потенциальная энергия внешних сил.
Из условий стационарности функционала (6) следуют уравнения равновесия, зависимости Коши и граничные условия в напряжениях. В конечно-элементном подходе тело V, в котором разыскивается решение, разбивается на r частей так, чтобы в каждой части материальные свойства были непрерывны. Часть тела с номером k разбивается на n конечных элементов. Решение для перемещений разыскивается в классе непрерывных функций во всем теле V, а для деформаций – в классе функций, непрерывных в отдельных частях. Через U обозначается глобальный вектор узловых перемещений, а через Fk – глобальный вектор узловых деформаций k-й части. Аппроксимация векторов перемещений и деформаций внутри элемента с номером e принимается в виде ue = NeU, £e = MeFk, (7)
где Ne и Me – матрицы функций форм элемента.
Условия стационарности функционала (6) по деформациям представляют собой r уравнений
GkU - SkFk = 0, k = 1,2,...r,(8)
в которых nk
G e = J BeTDeMedv , Gk = ^ G e ,
Vеe nk
Se = J MeTDeMedv, Sk = £ Se ,
Vee
Be – результат действия оператора L на Ne . Из системы уравнений (8) можно найти векторы деформаций
Fk = SkGTU .(9)
Таким образом, применение смешанной конечно-элементной схемы решения упругой задачи позволяет выразить узловые деформации (а, следовательно, и узловые напряжения) через узловые перемещения без применения операции дифференцирования приближенного решения.
Процедура итерационного построения решения состоит в следующем. На заданной конечно-элементной сетке с использованием смешанного подхода строится решение (нулевое приближение) поставленной выше задачи. При этом из равенств (1)–(5) в построении решения участвуют лишь условия на контуре конструкции. При подстановке во все алгебраические равенства полученного решения вычисляется вектор невязок, величина которого характеризует точность выполнения этих условий. С целью уменьшения величины вектора невязок соотношения (1)–(5) представляются системой уравнений относительно перемещений в основных узлах (основными объявляются узлы сетки, в которых должны выполняться алгебраические равенства), перемещения в остальных узлах принимаются равными значениям из нулевого приближения. Найденные основные перемещения принимаются за граничные условия в основных узлах на следующем шаге итерационного процесса. Тем самым граничные условия в напряжениях и условия непрерывности напряжений и деформаций по линии контакта преобразуются в граничные условия в перемещениях. Далее процесс повторяется.
Заметим, что уточнение решения на очередном шаге итерации сводится к решению обратной задачи – поиску перемещений в основных узлах, обеспечивающих минимум вектора невязок.
Описанная процедура последовательных приближений оказывается сходящейся. Зависимость решения от конечно-элементной сетки уменьшается с ее сгущением. Выход из итерационного процесса осуществляется при достижении величиной невязки заданного значения или при стабилизации решения. Полученный результат оценивается по значению коэффициента улучшения решения k , равного отношению среднеквадратичного значения величины вектора невязок в нулевом приближении к соответствующему значению в итоговом решении.
3. Анализ вычислений
На рисунках, приведенных ниже, представлены результаты вычислений напряжений вблизи особой точки А, полученные по описанной в п. 3 итерационной процедуре. Материальные параметры для более жесткого эле- мента конструкции не менялись – E = 206 -1
ГПА , ν = 0.3, α = 0.11е-4 град- , в менее жестком элементе коэффициент Пуассона и коэффициент температурного расширения рав -1
ны ν = 0.25, α = 0.85е-5 град- , а модуль Юнга варьировался.
чениям, определяемым равенствами (4–5). Заметим также, что левые (крайние) точки графиков являются значениями соответствующих параметров в нулевом приближении (ANSYS-решения), поэтому эти величины характеризуют погрешность решения в нулевом приближении.
б
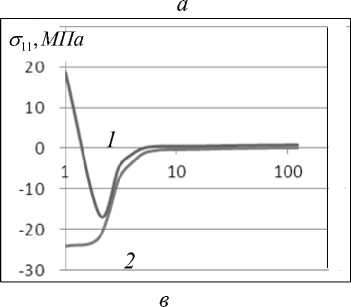
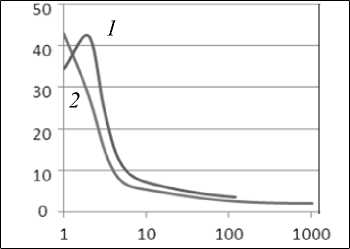
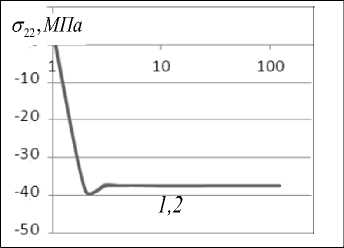
Рис. 2. Значения параметров решения в зависимости от числа итераций ( E = 30 ГПа):а) величина вектора невязок (1 – для числа узлов КЭ-сетки 4171, 2 – для 7912; б) 1– напряжения σ 2 (1 2 ) и 2 – σ (2) в точке А; в) напряжения 1– σ (1) и 2 – σ (2) в точке А; г) напряжения 1– σ (1) и 2–
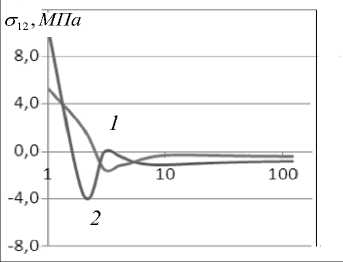
г
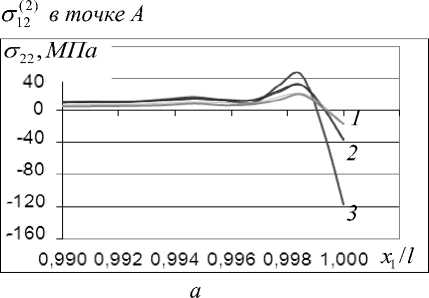
2– E = 30 Га; 3– E = 70 ГПа ); б) поверхность напряжений ( E = 30 ГПа)
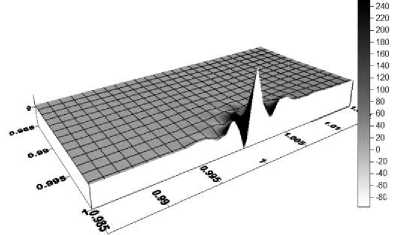
Рис. 3. Напряжения σ (1) и σ (2) вблизи особой точки: а) на линии соединения (1– E = 15 ГПа;
Приращение температуры во всех расчетах принималось одинаковым – Δ T = 1000 C .
Из рис. 2 видно – все параметры решения с ростом числа итераций стремятся к зна-
На рис. 3 кривые σ(1) и σ(2) совпадают для всех трех значений модуля E . В особой точке эти напряжения имеют значения, определяемые равенством (5). При этом, как сле- дует из этого равенства, если выражение (ν E -ν E ) стремится к нулю, напряжения
σ(1) и σ(2) неограниченно возрастают. Наи- большее напряжение возникает не в самой точке А, а в ее окрестности на свободном контуре в более жестком элементе (рис. 3б). Об- ласть значительного изменения напряжений
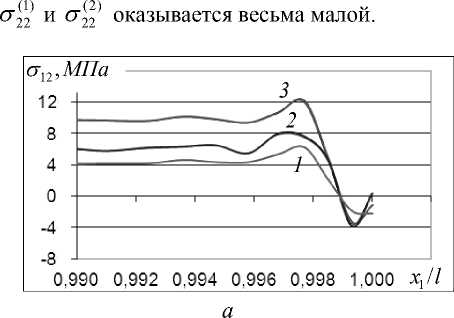
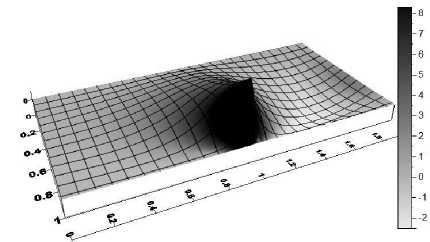
Рис. 4 . Напряжения σ (1) и σ (2) вблизи особой точки: а) на линии соединения (1– E = 15 ГПа;
2– E = 30 ГПа; 3– E = 70 ГПа); б) поверхность напряжений ( E = 30 ГПа)
изменения в малой окрестности особой точки и стабилизируются с удалением от нее.
При этом напряжения σ вне малой окрестности точки А оказываются положительными в элементе с меньшим коэффициентом температурного расширения и отрицательными – с большим.
б
На рис. 4а напряжения σ (1) и σ (2) в различных элементах представляются одной кривой, так как они практически совпадают. Эти напряжения претерпевают значительные изменения в малой окрестности особой точки и монотонно уменьшаются с удалением от нее. При этом наибольшие значения напряжения σ (1) и σ (2) достигают на линии соединения элементов конструкции.
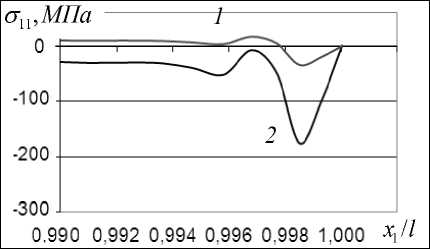
Рис. 5. Напряжения σ (1) и σ (2) на линии соединения вблизи особой точки ( E = 30 ГПа )
На рис. 5 представлены нормальные напряжения σ (1) и σ (2) в составной пластинке. Эти напряжения претерпевают существенные
Заключение
С использованием численно-аналитического итерационного конечно-элементного подхода в условиях плоской задачи изучены напряжения вблизи особой точки составной пластинки при ее однородном температурном нагружении. Показано, что все параметры состояния конструкции в малой окрестности особой точки претерпевают значительные изменения. Сформулировано условие для материальных параметров составляющих элементов, при котором особая точка оказывается сингулярной.
Алгоритм реализован на языке Фортран-90, компилятор Intel 11.0, расчеты выполнялись на суперкомпьютере ТЕСЛА-ПГУ НОЦ ПиРВ.
Список литературы Температурное нагружение составной конструкции в условиях плоской задачи
- Варданян Г.С., Фриштер Л.Ю. Моделирование термоупругих напряжений в составных конструкциях//Изв. АН АРМ. ССР. Механика. 1986. Вып. XXXVIII, № 6. С. 310.
- Савостьянов В.Н., Фриштер Л.Ю. Моделирование кусочно-однородной задачи механики деформируемого твердого тела методом фотоупругости/Изв. нац. АН респ. Армения. Механика твердого тела. 1993. № 6. С. 38-43.
- Фриштер Л.Ю. Расчетно-экспериментальный метод исследования напряженно-деформированного состояния составных конструкций в зонах концентрации напряжений: дисс.. д. техн. н. 2009. 391 с.
- Алексанян Р.К., Мкртчян А.М. Температурные напряжения в составном прямоугольнике//Изв. нац. АН респ. Армения. Механика. 1970. Т. 23, № 4. С. 3-11.
- Чобанян К.С., Алексанян Р.К. Термоупругие напряжения в окрестности края поверхности соединения составного тела//Изв. нац. АН респ. Армения. Механика.1971. Т. 24, № 3. С. 22-32.
- Алексанян Р.К. Термоупругие напряжения в составной полуплоскости//Изв. нац. АН респ. Армения. Механика. 1971. Т. 24, № 4. С. 45-54.
- Haojiang D. The analysis of thermal residual stresses near the apex in bonded dissimilar materials//Int. J. of Solid and Structures. 1999. Vol. 36, № 36. P.5611-5637.
- Yang Y.Y., Munz D. Stress singularities in a dissimilar materials joint with edge tractions under mechanical and thermal loadings//Int.J. of Solid and Structures. 1997. Vol. 34, № 10. P.1199-1216.
- Вейцман Р.И. Концентрация термоупругих напряжений вблизи стыка разнородных материалов//Исследование температурных напряжений. М.: Наука. 1972. С.41-151.
- Xiang-Fa Wu, Robert A. Jenson. Stress-function variational method for stress analysis of bonded joints under mechanical and thermal loadings//Int. J. of Eng. Science. 2011. Vol. 49, Issue 3. P. 279-294.
- Barut A., Guven I., Madenci E. Analysis of singular stress fields at junctions of multiple dissimilar materials under mechanical and thermal loading//Int. J. of Solid and Structures. 2001. Vol. 38, № 50-51. P. 90779109.
- Пестренин В.М., Пестренина И.В., Ландик Л.В. Напряженное состояние вблизи особой точки составной конструкции в плоской задаче//Вестник Томского гос. ун-та. Математика и механика. 2013. №4(24). С.78-87.
- Пестренин В.М., Пестренина И.В. Механика композитных материалов и элементов конструкций. Пермь: Изд-во Перм. гос. ун-та, 2005. 364 с.


