Теоретические исследования нестационарных влагофизических процессов в ограждающих конструкциях зданий

ограждения среды и могут иметь сильно отличающиеся значения при положительных и отрицательных температурах. Следовательно, рассмотрение нестационарных процессов переноса тепла и влаги в многослойных неоднородных конструкциях, особенно на предпроектных этапах, по-прежнему актуально и необходимо для предварительной оценки тепловой защиты многослойных ограждающих конструкций в эксплуатационных (нестационарных) условиях.

В исследованиях автора [2, 3, 4] разработана физико-математическая модель для имитационного моделирования на ЭВМ совместного тепловлагопереноса в нестационарном режиме и показана экономическая целесообразность применения пеноизола и пенополистирола в качестве среднего теплоизоляционного слоя в трехслойных ограждающих конструкциях. Однако в последнее время строители все меньше доверяют теплоизоляционным материалам из пенопластов - при всех положительных качествах они имеют один недостаток - низкую огнестойкость. Кроме того, при нагревании до температуры выше 80 °С они могут оплавляться и выделять токсичные вещества.

Целью настоящих исследований является адаптация физико-математической модели нестационарного тепловлагопереноса для исследования трехслойной ограждающей конструкции с несущим и декоративным слоями из силикатного кирпича и средним (теплоизоляционным) слоем из базальтовой ваты - все материалы местного производства.

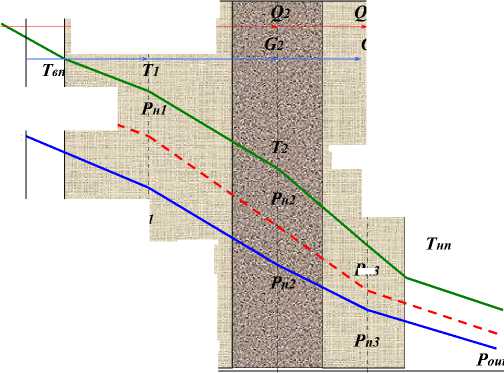
На рисунке 1 показана схема исследуемой конструкции с обозначением теплофизических характеристик материальных слоев и характерных границ: I - граница между воздухом помещения и внутренней поверхностью первого слоя ограждения (1 - несущий слой из силикатного кирпича); II - граница между 1-м и 2-м слоями (2 - теплоизоляционный слой из базальтовой ваты); III - граница между 2-м и 3-м слоями (3 - декоративный слой из силикатного кирпича); IV - граница между наружной поверхностью 3-го слоя и наружным (атмосферным) воздухом.

Математический аппарат модели разработан с учетом того, что теплофизические характеристики материальных слоев конструкции (теплоемкость, теплопроводность, температура) принадлежат оси слоя, следовательно, проводимость между слоями характеризуется сопротивлением теплопроводности между осями слоев. На границе I приняты нормативные температура и относительная влажность воздуха в помещении - ф , T_in , на границах II и III предусматривается равенство тепловых потоков и температур, а на границе IV приняты переменные параметры окружающего воздуха - Т_оифр_ош (климатические условия г. Читы).

Также на рисунке 1 показаны потоки тепла и влаги (в паровой фазе) с допущением, что при нестационарном режиме процесс теплопередачи происходит от внутреннего воздуха помещения к наружному (одномерная задача - по оси Ох).

Процесс нестационарной передачи тепла ( Q ) в толще слоев ограждения определяется двумя законами: проводимости (закон Фурье) q = -^.— и аккумуляции тепла dQ_aK = с ■ dx ■ dT д х

Количество тепла Q i , передаваемое от центра i -го слоя (толщиной d i. , с температурой в 2

центре T ) к центру следующего за ним ( i+1 ) слоя (толщиной di + 1 , с температурой в центре '                                                                                                   2

T ), согласно принятым граничным условиям определится из выражения

Q i =

( T - T + 1 ) d + d + . 2 ^  2 ^.₊₁

Коэффициент теплопроводности капиллярно-пористых тел, которыми являются многие строительные материалы, существенно зависит от влажности материала. Эту зависимость можно представить в виде [7].

T

O

2 слой,

3 слой,

Р

( С 2, d 2 ,X 2 , р 2, ( С 3, d 3 , X 3 , p 3,

Ц 2, b 2 )

Ц ³ , b³ )

тепло пар

T 3

G 1

I

SB

G 3

T in

Р н3

T out

Р inн

Р in

I

IV

II

III

Рисунок 1 - Схема трехслойной ограждающей конструкции для совместного тепловлажностного

Р п1

мЯ-

x

расчета в нестационарном режиме: d i , d 2 , d з - толщина слоев конструкции [м]; c i , С 2 , с з - теплоемкость слоев [|<Дж/(кг " С)]; p i , р 2 , р з - плотность материала слоев [кг/м³]; X i , Х 2 , Х з - коэффициент теплопроводности материала слоев [Вт/(м-^оС)]; p i , ^ 2 , р з - коэффициент паропроницаемости материала слоев [кг/(м-с - Па)]; P i , Р 2 , в з - коэффициент влагопроводности материала слоев [кг/(м-с)]; T i , Т 2 Т - температура на оси 1, 2 и 3 слоя соответственно [^оС]; Т вп , Т нп - температура на внутренней и наружной поверхности ограждения соответственно [^оС]; Р п1 , Р п2 , Р пз - парциальное давление воздуха на оси 1, 2 и 3 слоя соответственно [Па]; Р н1 , Р н2 , Р нз - давление насыщенного пара воздуха на оси 1, 2 и 3 слоя соответственно [Па]; P in , P out - парциальное давление пара внутреннего воздуха (помещения) и наружного воздуха (климат г. Читы) соответственно [Па]

Г 7 \ 4 = 4 1 1 + w — I, w c I        100 J

где 4 - теплопроводность сухого материала; W - весовая влажность материала (влагосодер-жание), %; Z - коэффициент приращения теплопроводности на 1 % влажности, определяется экспериментальным путем индивидуально для каждого материала.

Численные значения коэффициента Z (табл. 1) для силикатного кирпича плотностью 1700 кг/м3 были получены аппроксимацией табличных данных, приведенных в [6], а для базальтовой ваты плотностью 80 кг/м3 - в результате экспериментальных исследований в лаборатории «Строительные материалы» ЗабИЖТ по методике, разработанной автором в [2].

Таблица 1

Зависимость коэффициента теплопроводности от влажности материалов

Наименование строительных материалов	Прирост Z на 1% влажности
Кирпич силикатный плотностью 1700 кг/м3: - при положительной температуре окружающего воздуха - при отрицательной температуре окружающего воздуха	3 5,5
Базальтовая вата	2

При прохождении теплового потока через толщу i -го слоя ограждения часть тепла аккумулируется материалом слоя, изменяя при этом его температуру на ΔТ , определяемое как разность температур т* в период t и T ^{- 1} в период ( t - 1) . Рассматривая тепловой баланс поступления и потери тепла каждого слоя, определяем температуру в его центре по формуле:

Qi = Q

t - 1

i

Q - Q .

in out c. ■ p. ■ d.

iii

где Q in - входящий поток тепла, равен выходящему с предыдущего слоя согласно принятым граничным условиям; Q out - выходящий поток тепла (равен входящему на следующий слой).

Разница Qin - Qout показывает количество теплоты, аккумулируемое слоем, за счет кото- рого происходит изменение температуры материала.

Влагопередача в ограждающих конструкциях происходит путем переноса влаги, находящейся в паровой фазе - за счет разности парциальных давлений, и переноса капельной влаги - за счет разности влагосодержаний.

Процесс переноса влаги в паровой части определяется паропроницанием и сорбцией-десорбцией материала.

Количество паровой влаги Gi, передаваемое от центра i-го слоя (толщиной d, с парци- альным давлением в центре Рп) к центру следующего за ним (i+1) слоя (толщиной d+1, с пар-

2 циальным давлением в центре P ni+i ), согласно принятым граничным условиям определится из выражения

(Pm - Pn.+1) .(4)

‘      d i + d .

2M.

Парциальное давление определяется в соответствии с законом Бойля-Мариотта по формуле

P . = P ■ ф., niнi где фi - относительная влажность на i-м слое, %; Рн - давление (упругость) водяного пара в насыщенном воздухе, Па.

Эмпирическая зависимость давления водяного пара в насыщенном воздухе в зависимости от изменения температуры от -41 до +30 оС получена в [2] и имеет вид

P = 0,0213 Т ³ + 1,69 Т ² + 48,02 Т + 611 .                             (6)

н

Диффузионный поток пара, проходящий через материальные слои ограждения, изменяет их относительную влажность W от нуля до максимального гигроскопического влагосодержа-ния Ws при относительной влажности - 100 %.

Взаимосвязь между сорбционной и относительной влажностью материала определена в [2] и выражается эмпирической зависимостью вида

Ws = А 1 ф + A₂ ф ² + A ф ,                                    (7)

где Ws - сорбционная влажность материала, %; ф - относительная влажность воздуха, отн. ед.; А_х, А ₂, А₃ - коэффициенты переменной.

Коэффициенты переменной в выражении (7) определяются экспериментально для каждого материала, так как сорбционные свойства обусловлены индивидуальными свойствами материалов. Для адаптации физико-математической модели нестационарного расчета для исследования ограждающей конструкции из силикатного кирпича с теплоизоляционным слоем из базальтовой ваты проведены экспериментальные исследования этих материалов по методике, приведенной в [2] и получены изотермы сорбции, показанные на рисунке 2, и численные значения коэффициентов переменной (табл. 2).

Увеличение влажности слоя материала до максимальной сорбционной вызывает появление капельной влаги, перенос которой в сечении ограждений характеризуется влагопроводно-стью за счет возникновения в материале градиента влагосодержаний V V .

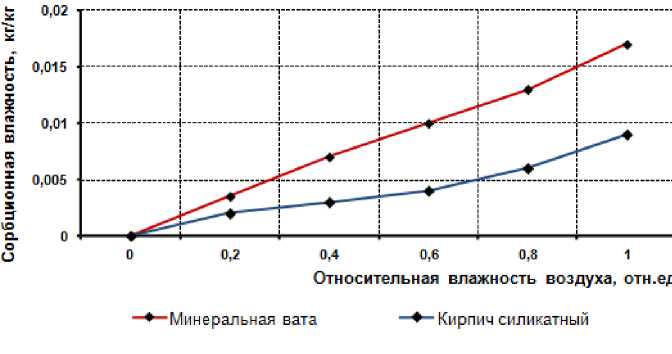
Рисунок 2 – Изотермы сорбции материалов трехслойной ограждающей конструкции

Таблица 2

Коэффициенты переменной в эмпирических зависимостях сорбционной влажности материалов от относительной влажности

Материал	Плотность, г/см3	Коэффициенты переменной
		А 1	А 2	А 3
Минеральная (базальтовая) вата	80	0,0075	-0,0105	0,0209
Кирпич силикатный	1700	0,0125	-0,0200	0,0120

Поток капельной влаги g , направленный от центра i -го слоя ограждения (с толщиной dr , с влагосодержанием в центре V i ) к центру следующего за ним ( i+1 ) слоя (толщиной d i + i , с 2 2 влагосодержанием в центре V i+1 ) согласно принятым граничным условиям определится из выражения

• V - - V + 1    ,                                                   (8)

• ^g1    d ₊ d .

2Д.  2Д. 1

где в — коэффициент проводимости влаги в материале, определяющий интенсивность переноса влаги, [кг/(м - с)].

Коэффициент влагопроводности в является переменным параметром, определяется экс- периментально и существенно зависит от содержания влаги в материале. Используя результаты исследований влагопроводности материалов, приведенные в [5] и методику обработки табличных данных, приведенную в [2], получили эмпирические зависимости коэффициента влагопроводности от весовой влажности для силикатного кирпича и базальтовой ваты вида в = BV + Bi,                                       (9)

где V – содержание капельной влаги в материале, %; В0 и B1 – константы, зависящие от вида материала.

Значения констант В 0 и B 1 для материалов ограждающей конструкции из силикатного кирпича с теплоизоляционным слоем из базальтовой ваты материалов приведены в таблице 3.

Таблица 3

Значения констант В 0 и B 1 в эмпирических зависимостях коэффициента влагопроводности от влажности материала

Наименование материала	Плотность кг/м3	В 0	В 1
Кирпич силикатный	1700	0,0098	0,006
Базальтовая вата	80	0,000006	-0,00012

Рассматривая изменение влажности материала слоя за счет притока и оттока паровой и капельной влаги в каждый момент счета, получили зависимость изменения относительной влажности в сечении i-го слоя ограждения ф = ф(t 1)

G - G , + g - ini       outi g ini

A + 2 A ф + 3 Аф'

^gouti .

Таким образом, для i-го слоя ограждающей конструкции на каждый момент счета температура на оси Тi определяет по выражению (6) значение давления насыщенных паров в се- чении слоя Рн, а относительная влажность на слое ф, получаемая из (10), определяет по выражению (5) значение парциального давления в сечении слоя Рпi

P ni = ф _i(O,02Y3Т ³ + 1,69 Т ² + 48,02 Т + 611) .                                  (11)

Выводы

В результате проведенных теоретических исследований получены эмпирические зависимости от температуры и влажности парциального давления насыщенных паров, сорбционной влажности, теплопроводности и влагопроводности, необходимых для компьютерного моделирования трехслойной ограждающей конструкции с несущим и декоративным слоями из силикатного кирпича и средним (теплоизоляционным) слоем из базальтовой ваты, с целью исследования совместных тепловлажностных процессов, протекающих в сечении конструкции в эксплуатационных (нестационарных) условиях.