Теоретико-игровая модель взаимодействия участников процесса создания онлайн-курсов в университете

Глобальные изменения в обществе (мировая пандемия [1], цифровая трансформация общества [2], промышленная революция и другие) [3] обеспечили толчок ускоренного развития цифровых образовательных ресурсов и, в частности, онлайн-курсов, используемых в системе высшего образования. По данным РБК1, выручка топ-100 участников рынка образовательных технологий (Edtech) в 2021 году составила 73 миллиарда рублей, продемонстрировав 70 % рост по сравнению с предыдущим годом. Большинство образовательных ресурсов сотрудничают с ведущими университетами, предоставляя преподавателям высшей школы платформы для создания и реализации массовых он-лайн-курсов, а студентам – возможность получить доступное дистанционное образование. Это мотивирует слушателей учиться в выбранном университете и пополняет ряды студентов. Национальная платформа открытого образования (openedu.ru), созданная Ассоциацией «Национальная платформа открытого образования», учрежденной ведущими университетами – МГУ им. М. В. Ломоносова, СПбПУ, СПбГУ, НИТУ «МИСиС», НИУ ВШЭ, МФТИ, УрФУ и Университетом ИТМО2, предлагает ОК по базовым дисциплинам, изучаемым в российских университетах.

Активное использование ОК в рамках университетского образования связано с целым рядом характерных особенностей, к числу которых следует отнести, в первую очередь, массовый характер использования электронных ресурсов по сравнению с традиционными технологиями оффлайн-об-учения. При этом расширение пользовательской аудитории, с одной стороны, увеличивает доходность образовательных проектов для университетов, а с другой стороны, повышает ответственность и риски, связанные, в частности, с возможным нарушением прав на объекты интеллектуальной собственности. Увеличение спроса на ОК приводит и к росту конкуренции, которая, в свою очередь, повышает требования к конкурентоспособности ОК как рыночного продукта [4, 5].

В этой ситуации взаимодействие между авторами учебных курсов (университетскими сотрудниками) и университетом может выходить за рамки типичной схемы «работник-работодатель», и более эффективными становятся различные формы партнерских отношений, в которых особую значимость приобретают вопросы разделения прав на результаты интеллектуальной деятельности (далее РИД) и доходов от их использования между партнерами. Часто подобные споры о разделении прав оказываются эмоционально окрашенными, что мешает рационально оценить РИД и будущие дивиденды. Для определения рационального поведения и решения спорных ситуаций в экономике, психологии и социологии используют теорию игр, инструменты которой позволяют провести стратегический анализ ситуации и определить эффективные решения. Цель нашего исследования – разработка теоретико-игровой модели взаимодействия между участниками процесса создания ОК, которая позволила бы выявить оптимальные (взаимовыгодные) варианты и условия партнерского взаимодействия авторов ОК и университета. Результаты исследования позволят сформировать обоснованную стратегию взаимовыгодного сотрудничества авторов онлайн-курсов и университета, найти или усовершенствовать формы их взаимодействия.

В данной работе будем рассматривать типовую ситуацию создания и коммерциализации ОК с участием университета и автора – университетского работника – в терминах и методологии теории игр. Характер взаимодействия университета и автора ОК позволяет отнести его к классу неантагонистических некооперативных конечных динамических игр с полной и совершенной информацией. Анализ решения игры позволит определить условия партнерских взаимоотношений между авторами ОК и университетом.

Особенности создания и реализации ОК

ОК представляет собой продукт, который выводится на рынок в условиях высокой конкуренции не только в коммерческом, но и в университетском секторе. Так, на платформе openedu3 в настоящий момент представлено 962 ОК по различным направлениям подготовки, в том числе более 100 по математике и механике, 43 по экономике и 54 по менеджменту. Такое предложение предъявляет высокие требования к конкурентоспособности ОК и обеспечению соответствующих компетенций и мотивации разработчиков [6, 7]. ОК – это высокотехнологичный продукт, в котором технологическая компонента формируется за счет как технологий обучения, так и технических решений, реализованных в образовательной платформе [8]. К числу передовых технологий, используемых в Edtech, относят, в частности, большие данные и искусственный интеллект, блокчейн, технологии VR и AR4. В целом, онлайн-образование становится все более интерактивным, развиваются тренды, ориентированные на персонализацию обучения, геймификацию, использование гибридных моделей обучения и других новых образовательных технологий5.

Анализ патентного ландшафта в данной области свидетельствует о том, что, несмотря на относительно невысокую патентную активность российских разработчиков, на зарубежном рынке в области цифровых образовательных технологий активно патентуются технические решения (см. рис. 1), среди них – средства контроля освоения образовательной программы, средства и инструменты прокто-ринга и другие цифровые технологии. В 2020 году, по сравнению с предыдущим годом, динамика

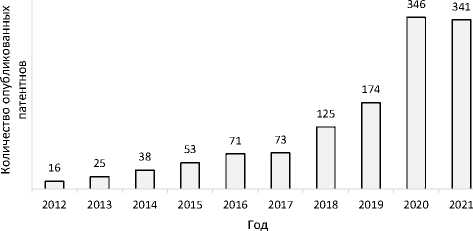
патентной активности демонстрирует почти двухкратный рост, как видно из рис. 1.

ОК как высокотехнологичный продукт по форме и содержанию представляет собой совокупность результатов интеллектуальной деятельности (РИД), включающую аудиовизуальные произведения, программы для ЭВМ, базы данных, а в некоторых случаях изобретения, полезные модели и промышленные образцы6. При этом модели коммерциализации данного продукта нередко основаны на использовании объектов интеллектуальной собственности или распоряжении интеллектуальными правами, а массовый характер использования ОК предъявляет высокие требования к правовой охране РИД, к мерам по предотвращению нарушения прав третьих лиц, а также к моделям распределения и закрепления прав на РИД между участниками процесса [4].

В сфере интеллектуальной собственности отношения между участниками процесса разработки и коммерциализации ОК проявляют себя с нескольких сторон. В первую очередь, это инструмент идентификации и фиксации прав на комплекс объектов ИС, реализованных в ОК. Весомый вклад в комплекс РИД, лежащих в основе ОК, вносит не только автор курса, но и университет, оказывая авторам поддержку в части использования образовательных технологий и дизайна курса. Во-вторых, интеллектуальные права – это универсальный инструмент управления процессом создания и реализации ОК, прежде всего – управления качеством курса через возможность участия авторов в доходах от его коммерциализации.

Продвижение на рынок и реализация ОК, как уже было отмечено выше, происходит в условиях высокой конкуренции, а контент и используемые технологии быстро устаревают, сокращая жизненный цикл ОК как рыночного продукта. Заинтересованность авторов в доходах от коммерциализации ОК существенно повышает их интерес в постоянном совершенствовании курса как в содержательном плане, так и в части использования новых образовательных технологий.

Таким образом, отношения между автором и университетом являются важным поведенческим фактором процесса создания ОК, что подтверждается и опытом авторов, и некоторыми публикациями [4, 7]. На первых этапах внедрения системы создания онлайн-курсов в УрФУ можно было наблюдать со стороны разработчиков наличие некого психологического барьера, связанного с необходимостью «расставаться» с исключительным правом на онлайн-курс. Однако по мере развития системы, роста уровня доверия и понимания ситуации со стороны авторов и университета, негативный эффект, связанный с данным фактором, был нивелирован, и в рамках нашей модели мы будем полагать, что участники процесса обладают достаточными знаниями в области интеллектуальной собственности для принятия рациональных решений. В этих условиях процесс создания и коммерциализации ОК становится более эффективным в рамках различных форм партнерства между авторами курса, университетом и другими участниками процесса. Особую значимость приобретает проблема выбора оптимальных решений в сфере разделения между партнерами интеллектуальных прав и доходов от их коммерциализации. При этом университет может играть в данной ситуации роль не только инвестора, но и участника инновационного проекта, выполняя часть «производственных» работ по дизайну и технической поддержке процесса создания, продажи и эксплуатации онлайн-курса. С точки зрения интеллектуальной собственности такое партнерство может быть реализовано в рамках целого комплекса вариантов разделения прав на ОК и доходов от его коммерциализации [8, 9]. Выбор оптимального варианта обусловлен как экономическими интересами сторон, так и их вкладом в создание курса.

Применение теории игр в решении задачи взаимодействия автора и университета

Для описания и анализа поведения агентов в микроэкономике, экономике общественного сектора, политэкономии и других разделах экономической теории широко используется теория игр [10]. В работе [11] представлен широкий обзор зарубежных исследований в области теоретико-игрового анализа инновационных процессов, проиллюстрированы основные направления приложений теории игр к анализу инноваций на разных уровнях организации инновационной деятельности: межорганизационном (игроками выступают фирма и ее конкуренты); мета-организационном (игроки – государственный институт и предприниматель); внутрифирменном (игроки – менеджер проектов или администратор ресурсов и сотрудники фирмы).

И. Н. Дубина обращает внимание на то, что в зарубежной литературе почти не представлены теоретико-игровые исследования инновационной деятельности на внутрифирменном уровне [11].

Именно он интересен нам для решения задачи взаимодействия автора онлайн-курса и университета. Задачи внутрифирменного уровня более детально рассмотрены в монографии Д. А. Новикова и А. А. Иващенко [12], где систематизированы некоторые классы теоретико-игровых математических моделей, применяющиеся в организационном управлении инновационным развитием фирмы. В работе [13] акцент сделан на процедурах принятия управленческих решений и не рассматривает непосредственно процесс создания инноваций. Другим примером моделирования инновационной деятельности как теоретико-игровой ситуации на внутрифирменном уровне является работа [13], где авторы моделировали процесс обмена знаниями между сотрудниками организации и показали, что поощрение каждого действия по обмену знаниями более эффективно, чем периодические организационные стимулы для поощрения поведения субъектов.

В нашем исследовании мы рассмотрели взаимодействие университета и автора, являющегося его работником, в процессе создания и коммерциализации ОК в терминах и методологии теории игр. При формировании и анализе теоретико-игровой модели мы будем пользоваться терминами, определенными в исследовании [14], основные из которых рассмотрены ниже.

Игра – это ситуация, в который каждый агент или игрок старается максимизировать свой выигрыш, выбирая наилучший план действий и учитывая зависимость результата от действий других игроков [14]. Стратегией игрока считается план его действий для всех возможных ситуаций. В самом простом случае в создании онлайн-курса участвуют два игрока – автор и университет. Определим особенности: 1) это парная игра с ненулевой суммой, в которой интересы игроков не противоположны; 2) это некооперативная игра (до начала игры агенты не имеют возможности заключения связывающих соглашений и договоров); 3) это игра с полной совершенной информацией (каждый игрок знает о правилах игры и платежах как своих, так и чужих); 4) игра динамическая и конечная (взаимодействие между агентами осуществляется в несколько периодов, количество которых ограничено). Динамические игры могут быть заданы деревом игры – графом, представляющим все возможные игровые состояния [15]. Вершины (узлы) дерева описывают все возможные позиции игроков, а ребра графа – все возможные ходы в каждой позиции [15]. Вершины (узлы) дерева игры, в которых заканчивается игра и определяются платежи, называются терминальными. Платежи (выигрыши)

определяют количественную оценку результатов игры для каждого игрока в денежных единицах. Решение игры – это набор оптимальных стратегий для игроков [16].

Наиболее распространенным принципом оптимального поведения в теории игр является концепция равновесия по Нэшу, которая была предложена математиком Джоном Нэшем в 1951 году. Равновесие Нэша определяется как набор стратегий, при котором ни одному игроку невыгодно отклоняться от выбранной стратегии при условии, что стратегии других игроков зафиксированы [17]. Эта концепция решения игры, по нашему мнению, достоверно описывает взаимодействие автора и университета в рамках создания ОК как игроков, заинтересованных в максимизации собственных платежей. Основная проблема с равновесием по Нэшу в динамических играх заключается в том, что в последнем периоде игры игроки могут вести себя иррационально. В момент, когда становится ясно, что данный период игры является последним, ранее выбранное действие может показаться иррациональным (не максимизирующим полезность) [14].

Избавиться от неправдоподобных предположений о стратегиях, сократив число равновесных ситуаций в динамических играх, позволяет концепция равновесия Нэша, совершенного на подыграх, которую предложил Рейнхард Зельтен в 1975 году. Подыгра – часть игры, начинающаяся с определенного узла. Набор стратегий игроков называется равновесием, совершенным по подыграм, если его сужение на любую подыгру данной игры есть равновесие Нэша в ней [17].

Согласно теореме Цермело, в конечной динамической игре с полной информацией всегда существует равновесие Нэша, совершенное на по-дыграх. В конечной динамической игре с совершенной информацией оно определяется методом обратной индукции [15]. Использование этого метода решения игры, даже если платежи не заданы в числовом виде, позволяет найти такие ограничения для них, чтобы один из наборов стратегий был решением игры [18].

Анализ ситуации для моделирования в рамках теории игр

Взаимодействие университета и авторов при создании и реализации ОК проявляется в распределении прав, затрат и доходов, связанных с созданием и реализацией онлайн-курса. При этом итоговый результат этого распределения зависит от действий каждого из игроков, что позволяет рассматривать данную ситуацию как игру. Исходя из опыта Уральского федерального университета, в таблице 1 выделены следующие формы и результаты взаимодействия университета и авторов при создании ОК.

Четыре формы взаимодействия автора и университета, представленные в таблице, определяют полный спектр вариантов распределения интеллектуальных прав, распределения доходов от коммерциализации ОК и участия сторон в его создании. Партнерство выделяется среди других форм взаимодействия «справедливым» распределением интеллектуальных прав и доходов от коммерциализации ОК, обеспечивающим совместное участие автора и университета в его создании.

Далее определим платежи классифицированной выше парной некооперативной динамической игры с полной совершенной информацией о взаимодействии университета и автора. Платежи хотя бы одного из двух игроков при всех приведенных в таблице 1 результатах взаимодействия зависят от востребованности ОК как рыночного продукта, поэтому описываемая игра неантагонистическая, интересы игроков не противоположны. Поскольку до начала игры любые связывающие договоры между университетом и автором отсутствуют, игра является некооперативной. Взаимодействие автора и университета до заключения соглашения о разделении прав, а также о распределении затрат и доходов может происходить в несколько периодов. Часто университет является работодателем автора, заинтересован в создании ОК и взаимодействует со многими авторами по заранее принятой стратегии. Ему принадлежит возможность первым сделать ход – предложить автору условия соглашения. Автор может как согласиться, так и отказаться от условий, которые предлагает университет для того, чтобы в последующих периодах предложить свои условия (подробнее в модели). Такую конечную динамическую игру можно представить в развернутой форме.

Заметим, что в процессе описываемой игры каждый игрок знает о предыдущих действиях как своих, так и других игроков, что соответствует определению игры с совершенной информацией. Информацию о платежах игроков (по крайней мере, об их качественной оценке) можно считать общедоступной, поэтому информация в такой игре будет полной.

Таким образом, взаимодействие университета и авторов в рамках создания и коммерциализации ОК можно рассматривать как неантагонистическую, некооперативную, конечную динамическую игру с полной и совершенной информацией.

Таблица 1

Варианты взаимодействия университета и автора

Variants of the interaction between the university and the author

Table 1

Условия взаимодействия	Формы взаимодействия
	Договор авторского заказа	Партнерство	Отчуждение автором исключительных прав на самостоятельно созданный ОК	Отсутствие взаимодействия
Распределение интеллектуальных прав	Университету принадлежит исключительное право, автору – только личные неимущественные права	Университету принадлежит исключительное право, автору – право использования и личные неимущественные права	Университету принадлежит исключительное право, автору – личные неимущественные права + может принадлежать право использования	Автору принадлежит исключительное право и личные неимущественные права, университету не принадлежит никаких прав
Участие университета в создании ОК	Университет содействует автору	Университет содействует автору	Университет не содействует автору	Университет не содействует автору
Возможность коммерциализации ОК университетом	Есть Университет получает полный доход от использования ОК	Есть Университет получает доход от использования ОК и выплачивает роялти автору	Есть Университет получает доход от использования ОК и выплачивает роялти автору	Нет Университет не может использовать ОК и не получает доход
Возможность коммерциализации ОК автором	Нет Автор получает разовое вознаграждение	Есть Автор получает роялти	Есть Автор получает роялти	Есть Автор использует курс самостоятельно
Уровень доходов университета от коммерциализации ОК	Соответствует востребованности ОК как рыночного продукта	Соответствует востребованности ОК как рыночного продукта	Соответствует востребованности ОК как рыночного продукта	Доход отсутствует, университет не может участвовать в коммерциализации ОК
Уровень доходов автора от коммерциализации ОК	Доход отсутствует, автор получает только разовое вознаграждение	Соответствует востребованности ОК как рыночного продукта	Соответствует востребованности ОК как рыночного продукта	Соответствует востребованности ОК как рыночного продукта

Теоретико-игровая модель взаимодействия автора и университета при создании онлайн-курса

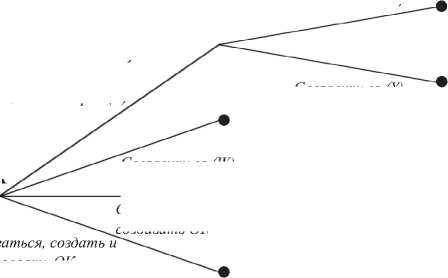
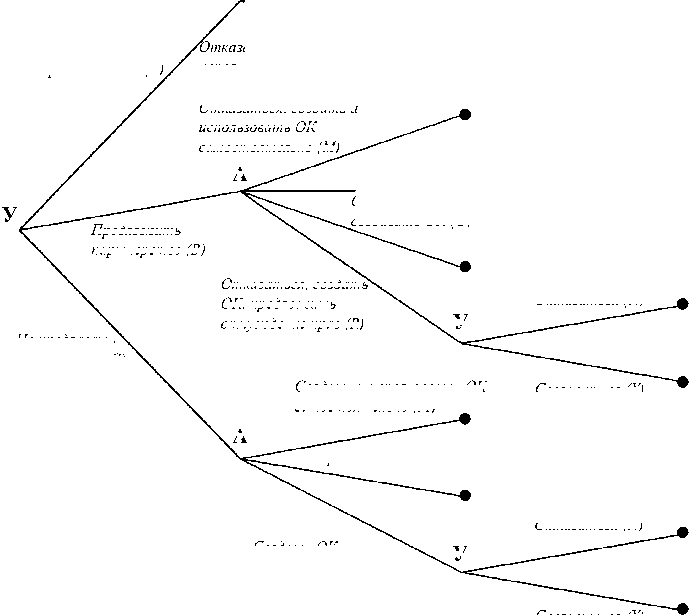
Представим дерево игры для взаимодействия двух игроков университета (У) и автора (А) в рамках создания и реализации ОК (см. рис. 2). Дерево игры визуализирует все возможные результаты взаимодействия университета и авторов, а также последовательность действий, которые могут к ним привести. Университет в такой игре совершает один или два хода, при этом, если университет выбрал стратегию AN, то он предлагает автору договор авторского заказа (A), а в случае предложения от автора об отчуждении прав университет откажется (N). Стратегия автора в такой игре должна содержать все возможные ответы на действия университета в первый ход, например, RWM – в случае предложения от университета договора авторского заказа автор создаст ОК сам и предложит университету отчуждение прав (R), (W) – в случае предложения сотрудничества автор согласится, на бездействие университета создаст и использует ОК самостоятельно (M).

Решение игры можно представить в виде набора оптимальных для игроков стратегий (У; А), где на первом месте стоит стратегия университета, а на втором – автора. Платежи игроков представлены в таблице 2, в различных терминальных вершинах дерева они будут отличаться.

При оценке параметров модели мы допустили, что при любой форме взаимодействия автора и университета доходы от использования ОК и издержки на его создание положительны, в случае договора авторского заказа авторское вознаграждение положительно.

Отказаться (N)

У

Отказаться, создать ОК, предложить отчуждение прав (R)

А

(b, 0

Согласиться (Y)

(d, e)

использовать ОК самостоятельно (M) Отказаться, создать и

(0, a)

Согласиться (W)

(0, 0)

Отказаться и не создавать ОК

(O)

(0, a)

(0, a)

(f, g)

(0, 0)

Отказаться (N)

Предложить договор авторского заказа (A)

А

У

А

У

Предложить партнерство (B)

Отказаться, создать

ОК, предложить отчуждение прав (R)

использовать ОК самостоятельно (M)

(0, a)

(b, 0

(0, a)

(0, a)

Согласиться (Y)

Не предлагать создание ОК (C)

Создать ОК, предложить отчуждение прав (R)

Согласиться (W)

Отказаться и не создавать ОК (O)

Создать и использовать ОК самостоятельно (M)

Не создавать ОК (O)

Согласиться (Y)

(0, 0)

Отказаться (N)

(b, 0

(У , А) - платежи игроков

Рис. 2. Теоретико-игровая модель взаимодействия автора и университета при создании ОК Fig. 2. Game-theoretic model of the university-and-author interaction when developing an online course

Таблица 2

Ожидаемые платежи взаимодействия автора и университета

Expected payments as a result of the university-and-author interaction

Table 2

Обозначение	Платеж автора/университета	Обоснование суммы платежа или расчетная формула	Примечание
a	платеж автора в случае самостоятельной разработки и использования ОК	a = R–P, где R >  0 и P >  0 – соответственно доход от использования и издержки на создание ОК автором самостоятельно	чистый доход автора от самостоятельного использования ОК, a e R
b	платеж университета в случае самостоятельного создания авторами ОК с последующим отчуждением прав	b = αR ∙ (1 – r ), где α > 0 – коэффициент равный отношению доходов от использования ОК университетом в случае отчуждения прав и доходов при использовании ОК автором самостоятельно; 0 <  r < 1 – ставка роялти	доход от использования ОК за вычетом роялти, b > 0

Окончание табл. 2

Table 2 finishes

Обозначение	Платеж автора/университета	Обоснование суммы платежа или расчетная формула	Примечание
c	платеж автора в случае самостоятельного создания ОК с последующим отчуждением прав в пользу университета	b ⋅ r c = α R ⋅ r = 1 - r	доход автора от роялти, c > 0
d	платеж университета в случае заключения договора авторского заказа	d = βR – S – γP , где β > 0 – коэффициент, равный отношению доходов от использования ОК в случае договора авторского заказа и доходов при использовании курса автором самостоятельно, 5 > 0- вознаграждение автора, у > 0— коэффициент, равный отношению издержек университета на создание ОК в случае заключения договора авторского заказа к издержкам автора в случае самостоятельного создания ОК	доходы от использования ОК за вычетом издержек на вознаграждение авторов и участие в создании ОК, d g R
e	платеж автора в случае заключения договора авторского заказа	e = S	авторское вознаграждение, e > 0
f	платеж университета в случае партнерства	f = μR ∙ (1 – r ) – ρP , где μ > 0 – коэффициент, равный отношению доходов от использования ОК в случае партнерства и доходов при использовании курса автором самостоятельно, р >0- коэффициент, равный отношению издержек университета на создание ОК в случае партнерства к издержкам автора в случае самостоятельного создания ОК	включает доход от использования ОК за вычетом роялти и издержек на участие в создании ОК, f g R
g	платеж автора в случае партнерства	g = μR ∙ r	доход автора от роялти, g > 0
h	платеж игрока в случае, если он не участвовал ни в создании, ни в использовании ОК	h = 0	нулевой доход и нулевые издержки

Различные стратегии игроков, как показано на рис. 2, могут приводить к неотличимым по результатам платежа терминальным вершинам.

В игровой модели получено пять видов терминальных вершин: 1) онлайн курс не был создан, доходов нет ни у одного игрока, в этом случае платежи нулевые (0, 0); 2) университет не участвовал ни в создании, ни в использовании созданного автором ОК, и автор самостоятельно использует ОК – платежи (0, а ); 3) автор создал курс самостоятельно и передал права университету по договору отчуждения, тогда платежи – ( b , c ); 4) заключение договора авторского заказа обеспечит игрокам платежи ( d , e ); 5) партнерское соглашение между университетом и автором предполагает платежи – ( f , g ).

Анализ игры взаимодействия автора и университета при создании ОК

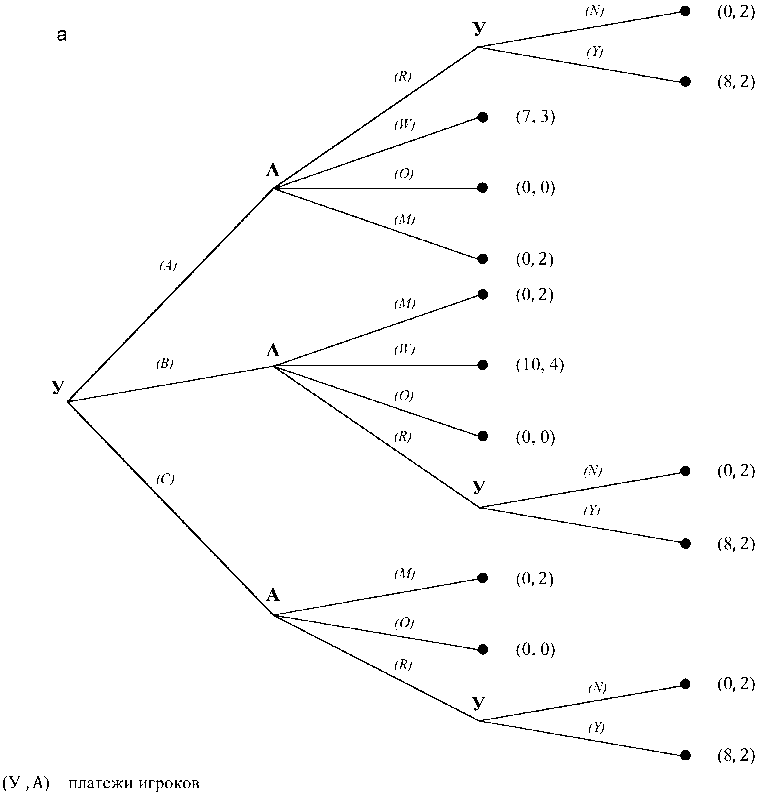
Рассмотрим пример решения игры, платежи заданы на рис. 3. Соотношение платежей соответствует опыту работы авторов статьи с Уральским федеральным университетом в рамках создания онлайн-курсов.

Пусть ожидаемый доход автора при самостоятельном использовании ОК: R = 4 у. е., издержки на создание ОК автором самостоятельно: P = 2 у. е., доход университета от использования курса в случае отчуждения автором прав в α = 2,5 раза больше, чем доход от использования курса автором самостоятельно, доход университета от курса, созданного по договору авторского заказа, в β = 4 раза больше, чем доход от использования курса автором самостоятельно, доход университета от использования курса при партнерстве в μ = 5 раз больше дохода от использования автором курса самостоятельно, издержки на создание курса университетом в γ = ρ = 3 раза больше, чем издержки на создание автором курса самостоятельно, авторское вознаграждение при договоре авторского заказа S = 3 у. е., ставка роялти r = 20 %.

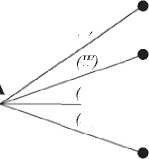
Найдем равновесие Нэша, совершенное на по-дыграх, методом обратной индукции (см. рис. 3) и определим профиль оптимальных стратегий. Всего в игре три уровня (этапа). Рассмотрим по-дыгру последнего уровня (рис. 3а), когда университет вынужден принять (Y) или отклонить (N) предложение об отчуждении прав автором. В такой подыгре университету выгодно согласиться на предложение автора для максимизации своего платежа и выбрать принять предложение (Y) с платежами (8, 2). Перейдем к подыгре предпоследнего уровня (рис. 3б), заменив подыгру последнего уровня на терминальную вершину с платежами (8, 2). В подыграх предпоследнего уровня выбирает автор: 1) согласиться ли на предложение университета, если предложение было сделано (W); 2) создать ОК и использовать его самостоятельно (M); 3) отказаться от предложения университета, чтобы создать ОК самостоятельно и потом предложить университету отчуждение прав (R); или 4) не создавать ОК вовсе (O). Автору в этом случае выгодно согласиться на предложение университета заключить договор авторского заказа (W), согласиться на предложение университета о партнерстве (W) и создать ОК самостоятельно, чтобы потом предложить университету отчуждение прав, если предложений от университета ранее не поступало (R). Заменим рассмотренные подыгры на терминальные вершины с платежами (7, 3), (10, 4) и (8, 2), соответственно.

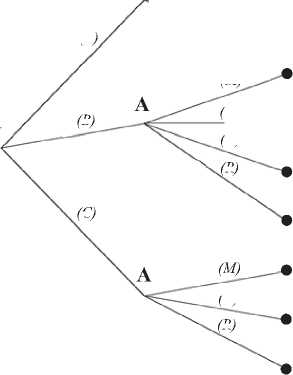
В исходной подыгре (рис. 3в) выбирает, какое соглашение предложить автору в рамках создания ОК: договор авторского заказа (А), партнерство (B) или не предлагать создание ОК (С). В рамках этой подыгры университету выгодно предложить автору партнерство (B).

Таким образом, стратегия университета, которая приводит к решению игры (BY) – предлагать автору партнерство и соглашаться в случае, если автор создал ОК самостоятельно и предлагает отчуждение прав. Оптимальная стратегия автора (WWR) – соглашаться на договор авторского заказа или партнерство, а в случае бездействия университета самостоятельно создавать ОК и предлагать отчуждение прав. Профиль стратегий (BY, WWR) является равновесием Нэша, совершенным на подыграх, и приносит игрокам платежи (10, 4). В нашем примере на числовых данных мы показали игру, в которой оптимальным результатом взаимодействия между университетом и автором при создании ОК является партнерство. Оценим соотношения платежей, заданных переменными, гарантирующие, что партнерство будет равновесием Нэша, совершенным на подыграх.

Определим условия, при которых оптимальным для участников итогом взаимодействия будут платежи ( f, g ). В подыгре последнего уровня университет предпочтет платеж b , т. к. b > 0. В по-дыграх предпоследнего уровня автор согласится на предложение университета о партнерстве, выберет ( f, g ), если { g >  c ; g >  a }. В исходной поды-гре университет предпочтет партнерство ( f, g ), если { f >  b ; f >  d }.

В результате анализа модели мы получили набор условий для платежей, по которому равновесием Нэша, совершенным на подыграх, оказался договор о партнерстве, оптимальный для обоих игроков:

e>c c>a g>c g>a f>b f>d

Партнерство как результат взаимодействия университета и автора в рамках создания ОК является оптимальным решением для игроков, если:

• 1.    Платеж авторов в случае партнерства ( g ) больше, чем в случае самостоятельной разработки и использования онлайн курса ( a ) или в случае самостоятельного создания ОК с последующим отчуждением прав в пользу университета ( c );

• 2.    Платеж университета в случае партнерства ( f ) больше, чем в случае заключения договора авторского заказа ( d ) или в случае самостоятельного создания авторами ОК с последующим отчуждением прав ( b ).

Проанализируем полученные условия оптимальности партнерства с точки зрения декомпозиции платежей.

μR ∙ r > αR ∙ r

μR ∙ r > R – P

μR ∙ (1 – r ) – ρP > αR ∙ (1 – r )

μR ∙ (1 – r ) – ρP > βR – S – γP

μR > αR

μR ∙ r >  R – P

μR ∙ (1 – r ) – ρP >  αR ∙ (1 – r )

μR ∙ (1 – r ) – ρP >  βR – S – γP

Доход от использования онлайн курса в случае партнерства ( μR ) должен быть больше дохода от использования курса, созданного автором самостоятельно и отчужденного в пользу университета ( αR ). Роялти автора курса в случае партнерства ( μR ∙ r ) должны быть больше, чем прибыль автора в случае самостоятельного создания и использования курса ( R ∙ P ).

(M)

А

(N)

(C)

У

(M)

А

(N)

У

а

(У , А) - платежи игроков

А

(A)

/     (B)

У

У

(M)

(N)

(Y)

(7, 3)

(0, 0)

(0,2)

(0,2)

(10, 4)

(0, 0)

(Y

(0,2)

(0, 0)

(Y)

(R)

(W)

(O)

(W)

(O)

(R)

(0,2)

(8,2)

(O)

(R)

(0,2)

(8,2)

(0,2)

(8,2)

б

(R)

(W)

(7, 3)

(0, 0)

(8, 2)

в

(A)

(O)

(M)

(M)

(B)

(C)

(R)

(R)

(10, 4)

(0, 0)

(8, 2)

(0, 2)

(0, 0)

(0, 2)

(0, 2)

(W)

(O)

(O)

(8, 2)

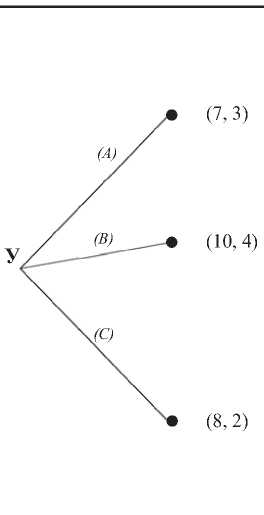
Рис. 3. Пример игры с заданными платежами (а – игра последнего уровня, б – игра предпоследнего уровня, в-исходная подыгра)

Fig. 3. An example of a game with given payments (a – game of the last level, b – game of the penultimate level, c – initial subgame)

Прибыль университета в случае партнерства ( μR ∙ (1 – r ) – ρP ) должна быть больше, чем в случае использования курса, созданного автором самостоятельно и отчужденного в пользу университета ( αR ∙ (1 – r )). Прибыль университета в случае партнерства ( μR ∙ (1 – r ) – ρP ) должна быть больше, чем прибыль университета в случае создания курса по договору авторского заказа ( βR – S – γP ).

Заключение

В качестве заключения отметим наиболее важные, на наш взгляд, результаты проведенного исследования и выводы.

• 1)    Показано, что онлайн-курс представляет собой высокотехнологичный рыночный продукт, который выводится на рынок в условиях высокой конкуренции и представляет собой совокупность результатов интеллектуальной деятельности, включающих аудио- и визуальные произведения, программы для ЭВМ, базы данных, а в некоторых случаях изобретения, полезные модели и промышленные образцы. Весомый вклад в комплекс результатов интеллектуальной деятельности, лежащих в основе ОК, вносит как автор курса, так и университет, оказывая авторам поддержку в части использования образовательных технологий и дизайна курса.

• 2)    Высказано предположение о том, что отношения между автором и университетом являются важным поведенческим фактором процесса создания ОК. В этой ситуации взаимодействие между авторами курсов (сотрудниками университета) и университетом может выходить за рамки типичной схемы «работник-работодатель». Более эффективными становятся различные формы партнерских отношений, в которых особую значимость приобретают вопросы разделения прав на результаты интеллектуальной деятельности и доходов от их использования между партнерами.

• 3)    Предложена теоретико-игровая модель типовой ситуации создания и коммерциализации ОК с участием университета и автора – работника университета. Взаимодействие университета и авторов в рамках создания и коммерциализации ОК рассмотрено как неантагонистическая, некооперативная, конечная динамическая игра с полной и совершенной информацией. Анализ модели выявил условия, при которых оптимальным оказывается партнерское взаимодействие авторов он-лайн-курсов и университета.

• 4)    Результаты исследования могут быть использованы университетом в качестве инструмента для обоснования и формирования стратегии

взаимовыгодного сотрудничества авторов онлайн-курсов и университета, а также для поиска или усовершенствования формы их взаимодействия. Партнерство является оптимальной стратегией для университета и автора, поскольку разделение затрат, интеллектуальных прав и доходов от использования ОК в рамках партнерства позволяет создать рыночный продукт лучшего качества, чем при самостоятельной работе автора или отсутствии у автора интеллектуальных прав и доли дохода от использования курса.