Теория акустического резонансного метода измерения сдвиговой упругости жидкостей

Акустический резонансный метод измерения низкочастотной (10? Гц) сдвиговой упругости жидкостей основан на использовании пьезокварцевого резонатора [1]. Кристалл пьезокварца в виде прямоугольного бруска контактирует верхней горизонтальной поверхностью с прослойкой жидкости, накрытой твердой накладкой в виде цилиндра. При тангенциальных колебаниях пьезокварца на основной резонансной частоте прослойка жидкости будет испытывать деформации сдвига и в ней должны установиться стоячие сдвиговые волны. Накладка при колебаниях пьезокварца будет практически покоиться, так как связь, осуществляемая прослойкой жидкости, слаба и не способна сообщить ей те большие ускорения, с которыми колеблется пьезорезонатор. Возрастание резонансной частоты пьезокварца свидетельствует о наличии сдвиговой упругости у прослойки жидкости. Если бы в прослойке действовали только диссипативные силы, то резонансная частота могла бы только уменьшаться. Таким образом, акустический резонансный метод основан на измерении влияния силы добавочной связи на резонансные свойства пьезокварца.

Теория акустического резонансного метода

Добавочная связь, осуществляемая прослойкой жидкости с расположенной на ней накладкой, будет выражаться в изменении резонансной частоты пьезокварца и затухания. Накладка с прослойкой жидкости находится на одном конце пьезокварца.

В работах [2—3] приравниванием импедансов жидкости и пьезокварца было получено выражение для комплексного сдвига резонансной частоты пьезокварца, обусловленного его взаимодействием через прослойку жидкости с твердой накладкой в виде:

Аю* ⁼ “      № * Я + m-ctg ^{ПП Н}),          (1)

Мх* н           тж где тж — масса жидкости, М = 2^рд. — масса пьезокварца, Н — толщина жидкой прослойки, %*— комплексное волновое число, со — циклическая частота. Последнее выражение приводится к более простому виду [2-5]:

_Дю* = ^MG*X* . 1 + со8(2х*Я-ф*)

Мт 8ш(2х*Я-ф*) ’ где ф* = ф'+/ф'' — комплексный сдвиг фазы, который происходит при отражении вязкоупругой волны от границы жидкость — накладка, S — площадь контакта прослойки жидкости с пьезокварцем, G* — комплексный модуль сдвига.

Зная, что G* =----— и %* = Р - /а , где р — действительная часть, а а — мнимая часть комплексного волнового числа, можно разделить выражение (2) на действительную со' и мнимую со" части [2-5]:

_ 25 ^5ЧЗ + СЯх)81п(2^^

Ю ” Мео           сН(2аЯ + ф") - соз(2ря - ф')           ’ д_ 25 (G"р - G'a)sin(2рЯ - ф') + (G" а + G'р) sh( 2аЯ + ф")

® ” Мго         сЬ(2аЯ + ф")-со8(2рЯ-ф’)

Для компонент комплексного сдвига фазы получены следующие вы ражения:

ф'= arctg

2Р ^|х*2 _ 5р „(.

5рж m

ф"= arcth

2а

'”|%*2| 5рж

5р^ m

Действительная часть комплексного сдвига фазы (5) показывает разность фаз между прямой и отраженной волной. Мнимая часть комплексного сдвига фазы (6) характеризует добавочное затухание, обусловленное потерей части энергии волны, передаваемой накладке.

Выражения для действительного (3) и мнимого (4) сдвигов частот значительно упрощаются в двух случаях. Если считать, что масса накладки пт достаточно велика и ее можно считать практически неподвижной, то в формуле (5) вторым членом знаменателя можно пренебречь и член т|х*²|

------» 20 и 2а. Следовательно, при отражении волны от границы ^Р ж жидкость — накладка сдвига фазы не происходит (ср = 0), что означает полное отражение энергии сдвиговой волны.

Если считать, что накладка отсутствует, т. е. m = 0. В этом случае знаменатель формулы (2) стремится к со, что соответствует изменению фазы на л^-, т. е. в этом случае ф' = 180°, ф" = 0. Это означает, что при отражении сдвиговой волны от свободной поверхности жидкости происходит потеря полуволны.

Если при колебаниях пьезокварца накладка покоится, то формулы (3) и (4) принимают следующий вид [2—5]:

_ 2S (О' р + G" a) sin 2рЯ + (G'a - G” р) sh 2аЯ

Мо        сЬ2аЯ-со82рЯ

_Дю„ _ 2S (G" Р - G' a) sin 2рЯ + (G” а + С Р) sh 2аЯ

Мо

сН2аЯ-соз2рЯ

Выражения (7) и (8) показывают, что при наличии комплексного модуля сдвига жидкости действительный и мнимый сдвиги частот являются функциями толщины прослойки, причем с увеличением последней мы должны наблюдать затухающие осцилляции Асо' и Асо’1.

Формулы (7) и (8) предельно упрощаются при малых толщинах прослойки жидкости, когда Н«Х — длины сдвиговой волны. В этом случае выражения для сдвигов частот принимают следующий вид:

Асо’=

Асо" =

2SG' МаН’ 2SG"

МтаН

(Ю)

При выводе этих формул рассматривалась половина длины пьезокварца, т. к. пьезокварц, закрепленный по средней узловой линии, состоит из двух одинаковых частей. Поэтому эти формулы справедливы для пьезокварца с прослойкой жидкости на обоих концах и с одинаковыми накладками. Если же жидкость с накладкой находится только на одном конце, то в формулах исчезает коэффициент 2 и для действительного и мнимого частей комплексного модуля сдвига, переходя к линейным частотам, будем иметь следующие расчетные формулы [2-5]:

^ХЦ'Н

(И)

4л2<0А/"Я где /0 — резонансная частота пьезокварца.

Из (И) и (12) следует, что при наличии у жидкости объемного модуля сдвига, А/' — действительный и А/ " — мнимый сдвиги резонансной частоты должны быть пропорциональны обратной величине толщины жидкой прослойки.

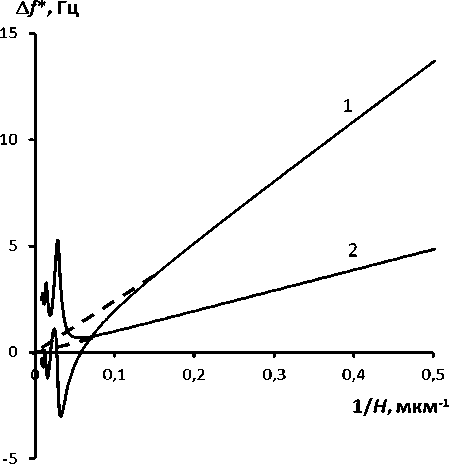
Рис. 1. Теоретические кривые зависимости действительного и мнимого сдвигов резонансной частоты пьезокварца Af (1) и Af” (2) от обратной толщины прослойки

Мнимый сдвиг резонансной частоты равен изменению затухания колебательной системы:

АГ~,             (13)

где Да — изменение ширины резонансной кривой пьезокварца. Тангенс угла механических потерь определяется:

G" _ Д/"

На рис. 1 показаны теоретические кривые зависимости Д/' и Д/" от обратной толщины пленки жидкости при G' = 0,25-10⁶ дин/см² и tgO = =0,35, рассчитанные по формулам (7) и (8).

Видно, что сдвиги частот пропорциональны обратной величине толщины жидкой прослойки. При увеличении толщины прослойки наблюдаются осцилляции сдвигов частот. Экстраполяция линейных зависимостей показывает, что обе зависимости стремятся к началу координат (пунктирные линии).

Таким образом, для измерения комплексного модуля сдвига жидкостей данным способом достаточно определить зависимости действительного Д/' и мнимого Д/" сдвигов частот от обратной величины толщины жидкой прослойки.

Таким образом, для измерения комплексного модуля сдвига жидкостей данным способом достаточно определить зависимости действительного А/' и мнимого А/" сдвигов частот от обратной величины толщины жидкой прослойки.

Приравнивая нулю производные по толщине от мнимого сдвига частоты (8), получим положения максимальных значений затухания в виде [2-3]:

Н — п,                      (15)

где нечетные значения п относятся к системе со свободной прослойкой, т.е. без накладки. При этом первый максимум затухания наблюдается при Н = X / 4. В случае с накладкой первый максимум затухания будет наблюдаться при толщине прослойки, равной X / 2.

Подставляя значения толщины по формуле (15) в выражение для мнимого сдвига частоты (8), можно получить закономерность изменения его максимальных и минимальных значений в виде:

Аютах = "Г?-----С1Ь(лй tg -) ,(16)

Jl/cocos 02

Л ,      5G'0 _ л® min = —----к th( ли tg -).(17)

/too cos 02

При 77 —> GO

Л " Л " Л "^(70

А“тах = 4in = А™= = Т7----К •(

Л/cocos О

Аналогичным образом для действительного сдвига частоты получим:

. , SG'0 0

Асо^ =----------tg — .(19)

Мсо cos 02

Из этих выражений видно, что с увеличением п осцилляции сдвигов частот постепенно исчезают (рис. 1), т. е. пьезокварц перестает чувствовать влияние отражений волны. В частности, при tg0 = 0,3 уже при и = 6 с точностью до 1% можно считать, что Aco_mav = Am . Формулы (13, 14) справедливы для случая, когда местом контакта накладки с прослойкой жидкости является один из концов пьезокварца. Можно показать, что сдвиг частоты, приходящийся на единицу площади, когда местом контакта является вся горизонтальная поверхность, равен половине сдвига частоты, приходящимся на единицу площади, когда местом контакта является конец пьезокварца. Поэтому

Асо^ G'0     е

—- =----—tg-,

5И    2Л/сосозО 2

Ао7_х _    (70

Sn 2MacosQ ’ где Sn — площадь всей горизонтальной поверхности пьезокварца. Для разности квадратов сдвигов частот получим следующее выражение:

с>2^'2п2

(Аш: )2 - (А< )2 =    " 2 Р (1 - tg2 -) .(20)

W“o)“cos-02

Учитывая, что р2 = °\Р cosO • cos2 — [2-4], для G'получим еледую-G’2

щее выражение:

С' = -^[(Ащ';)2-(Ао)^)2],(21)

Р ж или, переходя к линейной частоте:

с’= ^х-^Д ж У п <22)

Рж

Для тангенса угла механических потерь получается следующая расчетная формула:

2А/: АС (АС)²-(АС)²

Из этих выражений можно видеть, что при наличии сдвиговой упругости у жидкостей |ДС| всегда больше |ДС| • Если же жидкость ньютоновская при данной частоте, то ^Xf^ I = ^Х/^. |.

Данный способ определения комплексного модуля сдвига является наиболее простым в осуществлении. В этом случае необходимо после очистки рабочей поверхности пьезокварца нанести на нее достаточно толстый слой жидкости и измерить комплексный сдвиг резонансной частоты.

Экспериментальная проверка теории

Для проверки теории акустического резонансного метода измерены комплексные модули сдвига коллоидной суспензии наночастиц SiCT в полиэтилсилоксановой жидкости ПЭС-2 при толщине прослойки Н «X. В работе использован пьезокварц Х-18,5° среза с размерами 34,7x12x5,5 мм³ и массой 6,24 г, основная резонансная частота /₀ = 73,2 кГц. Площадь основания накладки 8=0,2 см². Нанопорошок диоксида кремния S1O2 получен методом газофазного синтеза (патент 2067077 Российская Федерация, МПК С01ВЗЗ/18). Коллоидная суспензия получена с использованием ультразвукового прибора Sonoswiss модели SW 1Н.

На рис. 2 приведены экспериментальные результаты измерения /Xf’ — действительного и /Xf” — мнимого сдвигов частот от обратной величины толщины жидкой прослойки для суспензий 81О2/ПЭС-2 (1,25%) с размером наночастиц 100 нм.

На рис. 2 видно, что зависимости действительного и мнимого сдвигов частот от обратной толщины прослойки линейны, что свидетельствует согласно формулам (11) и (12) наличие у данной суспензии объемного модуля сдвига, т. е. независящего от толщины прослойки. Расчеты по формулам (И) (12) дают значение для С=0,25-106 дин/см2 и для tg 0=0,35. Из рис. 1 и 2 видно хорошее согласие экспериментальных кривых с теоретическими.

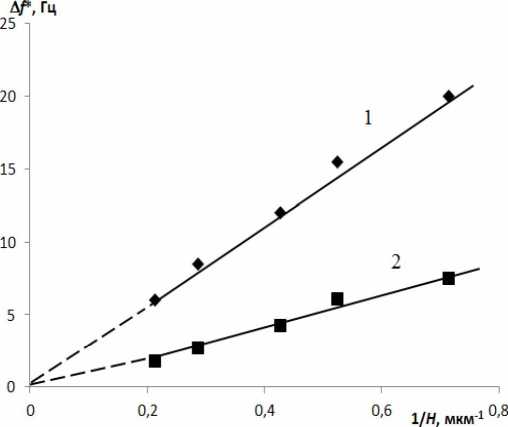
Рис. 2. Зависимость действительного (1) и мнимого (2) сдвигов частот от обратной толщины прослойки для суспензии 81О2/ПЭС-2 (1,25%) с размером наночастиц 100 нм

Также нами измерен действительный модуль сдвига этой же суспензии вторым способом, когда вся горизонтальная поверхность пьезокварца нагружена толстым слоем исследуемой жидкости. Измерение А/" дало значение 11 Гц. Значением ^' можно пренебречь, т. к. вклад вносимый им не превышает 2—3%. Расчет по формуле (22) дает значение для С=0,21106 дин/см2.

Значение G', полученное вторым способом, ниже значения, полученного первым способом. Это объясняется тем, что при нагружении пьезокварца толстым слоем жидкости рабочая поверхность пьезокварца используется не в полной мере, т. к. толщина слоя из-за мениска по краям меньше, чем в середине.

Дальнейшие экспериментальные исследования комплексного модуля сдвига широкого класса обычных, полимерных жидкостей и коллоидных суспензий показали наличие низкочастотной сдвиговой упругости в них [5-9].                                                                       '

Заключение

Из анализа решения задачи взаимодействия колебательной системы пьезокварц — прослойка жидкости — накладка получены выражения для комплексного сдвига резонансной частоты и комплексного сдвига фаз. Из теории метода следует два способа измерения сдвиговой упругости жидкости, которые реализованы в данной работе.

Первый способ реализуется при малых толщинах жидкой прослойки, когда Н « X . Второй способ основан на измерении предельного значения мнимого сдвига резонансной частоты пьезокварца, когда сдвиговая волна полностью затухает в толстом слое исследуемой жидкости. Удовлетворительное согласие результатов, полученных двумя способами, доказывают наличие низкочастотной сдвиговой упругости у исследованной жидкости.