Теория перехода из нематического состояния в смектическое

Первые теории, описывающие переход из нематического состояния в смектическое, были предложены Кобаяши [1–3] и Мак Миланом [4, 5]. В отличие от подхода, рассмотренного в этих теориях, мы не будем раскладывать межмолекулярный потенциал в ряд Фурье по векторам обратной решетки, поскольку он задан в бесконечной области и не является периодическим. Более того, разложение в работах [1–5] обрывается на первом же слагаемом без всяких обоснований. Неудивительно, что получаемые коэффициенты, участвующие затем в уравнениях среднего поля, не имеют физического смысла, а потому не могут быть оценены для реальных молекул. Глобальная проблема при описании перехода из нематического состояния в смектическое – это найти симметрийное соответствие между функцией распределения и потенциалом. Например, в теории Майера–Заупе [6, 7], описывающей переход из изотропной фазы в нематическую, это соответствие элементарно находится, поскольку как функция распределения длинных молекулярных осей, так и межмолекулярный потенциал имеют цилиндрическую симметрию относительно директора нематического порядка, поэтому противоречий не возникает. В упомянутых же теориях перехода из нематического состояния в смектическое периодичность, присущая плотности (функции распределения вдоль нормали к смектическим слоям), искусственно навязывается межмолекулярному потенциалу.

В данной работе введем такие функции распределения и параметры смектического порядка, которые имеют симметрию потенциала – цилиндрическую относительно директора нематического порядка. Для этого нам всего лишь понадобится перейти от интегрирования потенциала по объему к интегрированию по сферическим поверхностям с центром в середине молекулы. Мы увидим, что при таком подходе противоречий не возникает, и можно ввести такую аппроксимацию потенциала, коэффициенты в которой будут иметь физический смысл и могут быть оценены для реальных молекул. Также мы убедимся в том, что наклон в смектиках возможен только в случае присутствия в системе хиральности, в противном случае мы всегда будем получать структуры, цилиндрически симметричные относительно директора нематического порядка, а значит, наклона не будет. Эти хиральные слагаемые могут быть ничтожно малыми, но важен сам факт их присутствия, чтобы, скажем, молекулы смектического слоя, и без того попарно имеющие тенденцию к смещению друг относительно друга вдоль директора, выбрали все только одно из двух возможных направлений смещения.

Обобщение теории Майера-Заупе на случай перехода из нематической фазы в смектическую

Рассмотрим систему одноосных молекул, имеющих ориентационную функцию распределения f(a∙n) длинных осей a относительно директора нематического упорядочения n. В общем случае будем считать, что имеется неравномерное распределение плотности молекул в системе ρ(r). В частности, в нематической фазе плотность является постоянной величиной ρ(r) = ρ0, где ρ0– средняя плотность молекул в системе. Для простоты будем считать, что распределение плотности ρ(r) не зависит от ориентационной функции f(a∙n), и посмотрим, нельзя ли в этом простом случае описать переход из нематической фазы смектическую точно таким же образом, как это делается в теории Майера-Заупе [6, 7] для перехода из изотропной фазы в нематическую. Сво- бодная энергия молекулярной системы, обобщенная на случай неравномерного распределения плотности, может быть записана в следующем виде:

F = квТ JJ d 3r d 2a P (r) f (a ’n) ln [ p( r) f (a ’n)] +

+ 2JJJJd3r1 d2a1 d3r2 d2a2 P(rl ) f (al " n)P(r2) f (a2 " n)U12 (a1,a2,r12), где kB – константа Больцмана, T – температура, и Uef12(a1,a2,r12) – эффективный потенциал взаимодействия двух произвольных молекул, находящихся в точках 1 и 2. Первое слагаемое в формуле (1) представляет собой энтропию, а второе – внутреннюю энергию системы. Ориентационная функция распределения f(a∙n) в выражении (1) подчиняется условию нормировки

J d ² a f ( a • n ) = 1. (2)

Подставляя условия нормировки (2) в формулу (1), можем записать свободную энергию единицы объема системы вблизи точки 1 в следующем виде:

FV = к в Т P ( r i ) ln P ( r i ) + к в Т p ( г ) J d ² a f ( a • n ) ln f ( a ■ n ) + ⁺ 2 P ( r l ) JJJ d ³r 12 ^d 2 a 1 ^d 2 a 2 P ( r 12 ) ^f ( a l "  n ) ^f ( a 2 "  n ) U^ef ( a l , a 2 , ^r 12 ) ’

где мы стали отсчитывать положение точки 2 относительно точки 1, поскольку подынтегральное выражение не зависит от положения точки 2. Чтобы получить условие нормировки плотности ρ ( r ) и разделить функции ρ ( r ) и f ( a ∙ n ) в свободной энергии (3), воспользуемся тем обстоятельством, что при параллельной ориентации взаимодействующих молекул i и j (см. рис. 1), число ближайших соседей j у молекулы i не зависит от ориентации межмолекулярного вектора r 12 . Будем считать смещения молекул из положения бок-о-бок малыми по сравнению с длиной молекулы, в противном случае потенциал взаимодействия молекул резко убывает по модулю, и такие конфигурации дают малый вклад в статсумму. Тогда можем записать следующее условие нормировки:

— d 2 u ij P ( ^ ij ) = ^ 0 , a _i || a _j || n

Рис. 1. Скольжение двух

• (4)     молекул ЖК по поверх

ности друг друга где ξij – межмолекулярный вектор при заданном взаимном расположении молекул i и j с параллельными длинными осями на расстоянии соприкосновения молекул, вектор uij – единичный межмолекулярный вектор, а интегрирование проводится по поверхности соприкосновения молекул i и j. Величина σ0 имеет смысл числа ближайших соседей сбоку у произвольной удлиненной молекулы, которое, в случае плотных систем, примерно равно 2π ≈ 6. В качестве элементарного объема, в котором будем вычислять свободную энергию, рассмотрим объем, приходящийся на произвольную молекулу i в точке 1 и на все ее ближайшее окружение j при параллельной ориентации молекул i и j. Здесь и в последующем изложении будем считать отклонения длинных осей ai и aj друг относительно друга и относительно директора n малыми, в противном случае потенциал взаимодействия молекул резко убывает по модулю, и такие конфигурации дают малый вклад в статсумму. Свободная энергия такого элементарного объема получается интегрированием выражения (3) по поверхности соприкосновения молекул i и j вблизи точки 1:

NF = kBT —  d 2uy p (^ij) ln p (^ij) + kBT ст о J d 2a f (a • n) ln f (a • n) + ai||aj||n

⁺ 2 ° 0 JJJ d ³r 12

d2a1 d2a2 p(r12) f (al • n) f (a2 • n)Uf (al,a2,r12), где во втором и третьем слагаемых мы учли условие нормировки (4). Полная свободная энергия получается суммированием одинаковых элементарных свободных энергий (5) по всему объему. Обратимся к подынтегральному выражению в третьем слагаемом формулы (5). Попробуем разделить переменные интегрирования в этом выражении. Из четырех подынтегральных функций ρ(r12), f(a1∙n), f(a2∙n) и Uef12(a1,a2,r12) только эффективный потенциал Uef12(a1,a2,r12) резко убывает по модулю с увеличением расстояния r12 между молекулами и только функции f(a1∙n), f(a2∙n) и Uef12(a1,a2,r12) резко убывают по модулю с отклонением осей a1 и a2 от директора n. Тем самым, можем два раза воспользоваться методом перевала, поочередно вынося сначала функции ρ(r12), f(a1∙n) и f(a2∙n) из-под знака интеграла по r12, заменяя их значениями в точке соприкосновения молекул, а затем – вынося функцию ρ(r12) еще и из-под знаков интегралов по a1 и a2 и заменяя ее значением при параллельных молекулярных осях:

JU P ( ^r 12 ) f ( ^a 1 • n ) f ( a 2 • n ) U ef ( a l , ^a 2^{- r} 12 ) d 3 r 12 d 2 ^a 1 d 2 ^a 2

• (6)

• (7)

* — P ( ^ij ){JJ f ( al " n ) f ( a2 " n ) Ue2 ( a1, a2, u12 ) d 2a1 d ^2} d 2u12 a1||a2||n где

w

U 12 ^{( a} 1 , ^a 2 , ^u 12 ) - J U ef ^{( a} 1 , ^a 2 , ^r 12 ) ^r 12 d ^r 12 -

Подставляя выражение (6) в формулу (5) и минимизируя свободную энергию (5) независимо по ориентационной функции распределения f ( a ∙ n ) и по распределению плотности ρ ( r ) с учетом условий нормировки (2) и (4), получаем следующую систему уравнений:

f ( ^a 1 • ⁿ ) = "TexPГ 712J p ( ^u 12 • n ) [ f ( a 2 • n ) Uf yf ( a 1 , a 2 , ^u 12 ) d 2 a 2 ] d 2 ^u 12 I f I k B T

P ( ^u 12 • n ) = ' exP I _ρ

- ¹ ^ 7 J J f ( a 1 • n ) f ( a 2 • n ) UJ l! ( a 1 , a 2 , ^u 12 ) d ² a 1 d 2 a 2 I ,

2 kBT где ρ(u12∙n) определяется как плотность на расстоянии соприкосновения двух молекул, длинные оси которых параллельны друг другу и директору n, а нормировочные интегралы If и Iρ определяются следующим образом:

I f ^-J exP

’U 12 • n ) [ f ( a 2 • n ) U f ( ^a 1 , ^a 2 , U 12 ) d 2 a 2 ] d 2 U 12 I d 2 ^a 1 -

I P ^- J exP ] ¹ Г ¥ J J f ( a 1 ' ⁿ ) f ( a 2 ' ⁿ ) U ^ ef ( a 1 , a 2 , u 12 ) d ²a 1 d 2 a 2 I d 2 u 12 -

I ² k B T

Введем нематические параметры порядка степени ℓ согласно общеизвестному правилу: S i ^-J f ( a • n ) P i ( a • n ) d ²a ,

где Pℓ – полиномы Лежандра степени ℓ. Кроме того, введем смектические параметры степени ℓ согласно похожему правилу

° l ^- J P ( ^u 12 • ⁿ ) P l ( ^u 12 • ⁿ ) d 2 u 12 ,

где интегрирование проводится по поверхности соприкосновения молекул 1 и 2. Выясним физический смысл вновь введенных параметров смектического порядка на примере параметров σ 2 и σ 4 , которых, как мы увидим, вполне достаточно, чтобы описать переход из нематического состояния в смектическое. Для начала заметим, что в ненаклонной смектической A фазе, также как и в нематической, распределение межмолекулярного вектора u ₁₂ симметрично относительно направления нематического директора n . Это означает, что все смектические параметры нечетной степени равны нулю. Введем угол β между плоскостью, нормальной к нематическому директору, и межмолекулярным вектором u ₁₂ [см. рис. 1], т.е. угол, характеризующий смещение удлиненных молекул из положения бок-о-бок при идеальном нематическом порядке. Тогда ( u 12 ∙ n ) = sin β , и, согласно определению (11) средний квадрат и среднюю четвертую степень sin β при соприкосновении молекул можно записать следующим образом:

S sin ² в =

S sin ⁴ в =

2 σ 1

• 3    ° 0 ⁺ 3-

• 8σ4σ1

• 4    + — ² + -. 35 σ ₀7 σ ₀5

Заметим, что ни вторая, ни четвертая степени sin β не обязаны обращаться в ноль в изотропной и нематической фазах, поскольку в них усредняемые степени знакопостоянны. Также, написанные степени, вообще говоря, не обязаны обращаться в ноль в ненаклонной смектической фазе, по- скольку распределение межмолекулярного вектора u12 относительно нематического директора n может оставаться симметричным и при ненулевом среднем значении четных степеней sin β. Тем самым, сами по себе выражения (12) не могут быть количественными критериями перехода из нематической (или изотропной) фазы в смектическую. Однако в качестве простейшей меры смектического упорядочения можно ввести среднеквадратичное отклонение величины sin2β от- носительно ее среднего значения:

8 σ ₄

35 σ ₀

4 1 ст 2 |       8 ст 2     4

I +1,

9 / ст 0 J     63 ст ₀ 45

которое должно стремиться к нулю при идеальном смектическом упорядочении. Тем самым, если в результате нашей молекулярно-статистической теории мы получим фазовый переход, при котором дисперсия (13) существенно убывает и в дальнейшем стремится к нулю, то это можно интерпретировать как переход из нематической (или изотропной) фазы в смектическую.

Теперь вернемся к самосогласованным уравнениям (8)–(9) для ориентационной функции распределения f ( a ∙ n ) и распределения плотности ρ ( u 12 ∙ n ). Аппроксимируем эффективное взаимодействие U^ef 12 ( a 1 , a 2 , u 12 ) сферическими инвариантами T ℓLλ ( a 1 , u 12 , a 2 ) [8]:

U 12 ( a l , a 2 , u 12 ) = - ^ J lLX T lLX ( ^a 1 , ^u 12 , ^a 2 ) • ⁽¹⁴⁾

l, L , λ

Подставляя аппроксимацию (14) в формулы (8) и (9), используя известное свойство сферических инвариантов и определение параметров порядка (10), (11), домножая обе части первого уравнения в формуле (8) на Pℓ(a1∙n), а второго – на Pℓ(u12∙n), затем интегрируя обе части первого уравнения по всем возможным ориентациям вектора a1 и обе части второго уравнения – по всем возможным ориентациям вектора u12, и, наконец, обозначая за x в первом уравнении скалярное произведение (a1∙n), а во втором – скалярное произведение (u12∙n), получаем следующие рекуррент- ные соотношения для параметров порядка:

S 1/ S 0 = I IS ) / 1 0 S ) , ст i /ст о = I l ^CT )/ 1 ) ,

где напомним, что S 0 = 1 и число ближайших соседей σ 0 являются константами, а интегралы I ℓ ^{( S )} и I ℓ ^{( σ )} определяются следующими выражениями:

I IS ) = J P i ( x ) exP

I ^L l квТ

- 1

• 1                  I 1 ст„

• ¹1  ⁼J P l ⁽ x ) exp HTv[ ^{( J} 220 ⁺ J 022

  - 1             l ^{2 k}B T

"202 ^S 2 ⁺ J 220 ^{2 +} J 222 S 2 2 ⁺ J 242 σ ₀ σ ₀

S 2 ^ст 4 P ₂ ( x ) f dx , ^ст о J

^r₂₂₂ S 2 ) S 2 P₂ ( x ) + J ₂₄₂ S 2 P 4 ( x ) ] f dx ,

где сферические инварианты взяты вплоть до четвертой степени по L и вплоть до второй степени по ℓ и λ, полярное упорядочение длинных осей молекул отсутствует (т. е. отсутствуют инварианты с нечетными индексами ℓ и λ), и отсутствует хиральность (т. е. сферическими инвариантами с нечетными индексами L). Система уравнений (15) может быть решена численно, откуда могут быть получены зависимости параметров порядка Sℓ и σℓ от температуры. Для того чтобы решить численно систему (15), нужно знать аппроксимацию интеграла от эффективного потенциала по расстоянию сферическими инвариантами (14). Заметим, что нескольких выбранных сферических инвариантов, вполне достаточно, чтобы отразить все симметрийные особенности взаимодействия молекул, отвечающие за существование изотропной, нематической и смектической A фаз. Напомним, что для описания перехода из изотропной фазы в нематическую вообще достаточно одного слагаемого J202T202(a1,u12,a2) = J202P2(a1∙a2), описывающего анизотропию усредненного по расстоянию потенциала, т.е. зависимость его от угла между длинными осями молекул a1 и a2. Для того чтобы описать переход из нематической фазы в смектическую, оказывается необходимым дописать в потенциале слагаемые, явным образом зависящие от межмолекулярного вектора u12. Подставляя рекуррентные соотношения (15), (16) в формулу (5), получаем следующее выражение для элементарной свободной энергии:

2 - const + J 202 S 2 + ( J 220 + J 022 ) S 2 ² + J 222 S 2 ² + σ ₀ ²     22        σ ₀ σ ₀

+ J 242 S 22 " 4 - k B T In 1 0 ^s ) - k B T In 1 0" ) , σ ₀ σ ₀ σ ₀

в котором присутствуют только параметры порядка из формулы (15) и интегралы из формулы (16). Поскольку численные решения уравнений (15)–(16) подразумевают наличие фазовых переходов первого рода, то формула (17) может быть использована для сравнения свободных энергий в различных состояниях, одновременно удовлетворяющих минимуму свободной энергии (17), т.е. рекуррентным соотношениям (15)–(16).

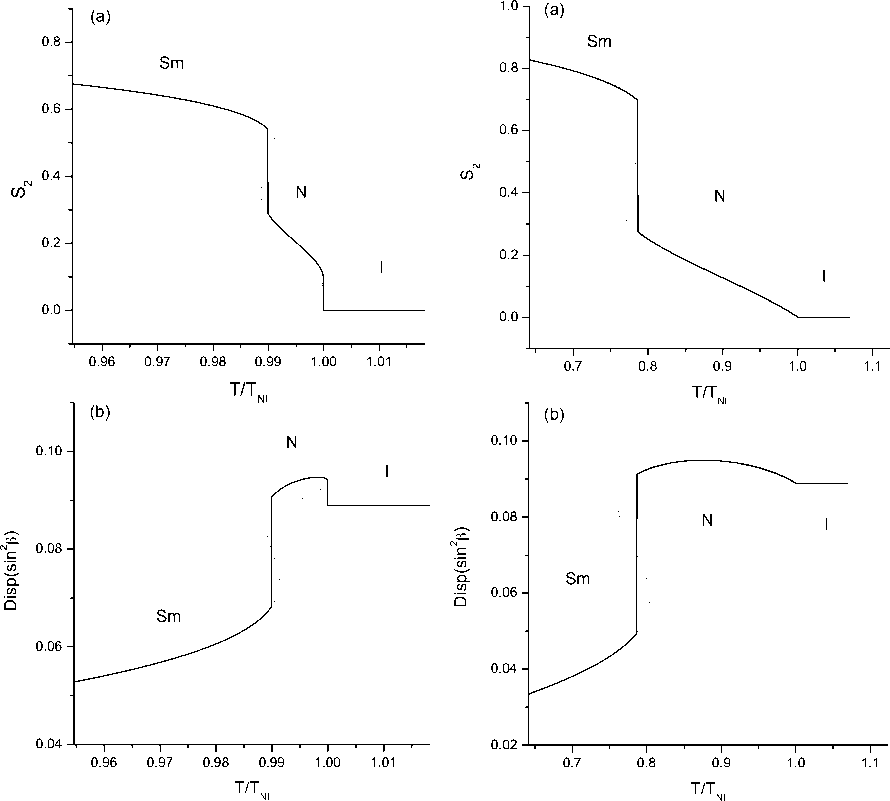
Рис. 3. Нематический порядок (a) и дисперсия межмолекулярных направлений (b) при J 220 = J 022 = 0,9 J 202 , J 222 = –3 J 202 , J 242 = –2 J 202

Рис. 2. Нематический порядок (a) и дисперсия межмолекулярных направлений (b) при J 220 = J 022 = 0,9 J 202 , J 222 = –1,1 J 202 , J 242 = –2,8 J 202

На рис. 2–5 приведены типичные зависимости параметра нематического порядка S2 и дисперсии квадрата угла β [см. формулу (13)], характеризующей смектический порядок, от температуры, согласно решению уравнений (15)–(16). На рис. 2 показан случай, когда происходит два фазовых перехода первого рода: из изотропной фазы в нематическую и из нематической в смектическую. Большие отрицательные значения коэффициентов J222 и J242 создают возможность сосуществова- ния нескольких решений уравнений для параметров порядка (15), часть из которых соответствуют устойчивому равновесию системы (минимум свободной энергии), а часть – неустойчивому (максимум свободной энергии). О наличии смектической фазы при температурах ниже обоих фазовых переходов можно судить по значению Disp(sin2β), которое резко падает при переходе из нематической фазы и стремится к нулю при дальнейшем уменьшении температуры, тогда как параметр нематического порядка S2 стремится к единице. Второй тип поведения параметров порядка приведен на рис. 3, когда переход из изотропной фазы в нематическую становится фазовым переходом второго рода, а переход из нематической фазы в смектическую по-прежнему остается фазовым переходом первого рода. При этом температурный разрыв между этими двумя переходами увеличивается по сравнению со случаем, приведенным на рис. 2. Такое решение реализуется, когда коэффициент J222 сильно увеличен по модулю по сравнению со случаем, представленным на рис. 2, а коэффициент J242 слегка уменьшен по модулю.

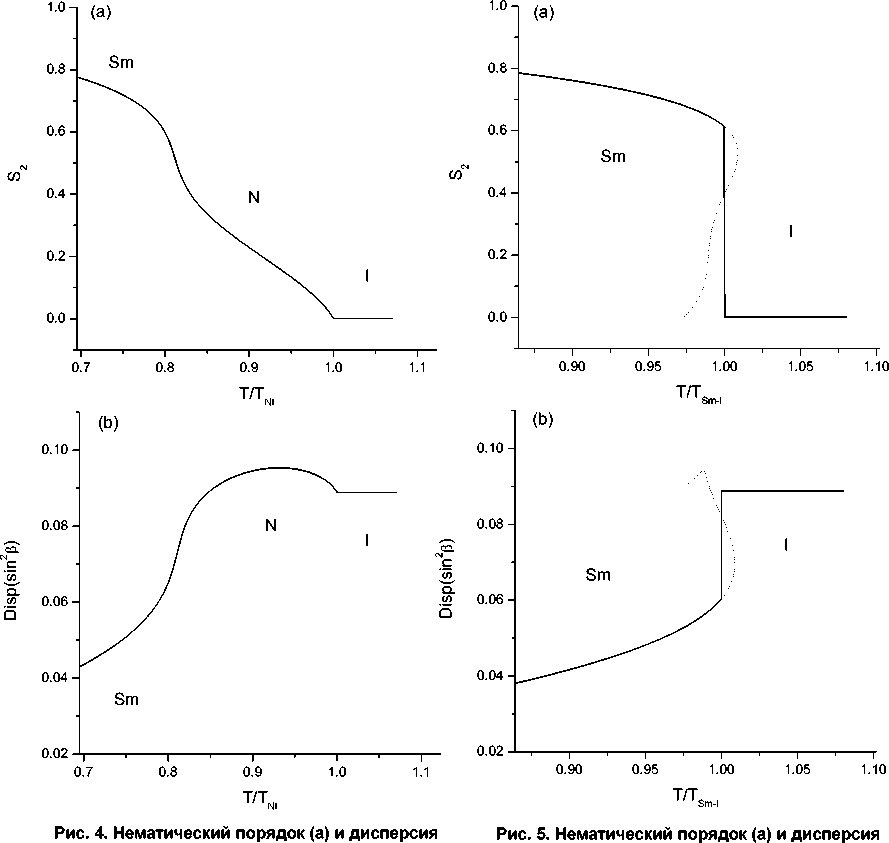
межмолекулярных направлений (b) при             межмолекулярных направлений (b) при

J 220 = J 022 = 0,9 J 202 , J 222 = J 242 = –2 J 202                  J 220 = J 022 = 0,9 J 202 , J 222 = –0,9 J 202 , J 242 = –2,8 J 202

Если оба коэффициента J222 и J242 примерно одинаковы и не сильно велики по модулю, то наблюдается третий тип поведения параметров порядка, приведенный на рис. 4, когда переход из нематической фазы в смектическую также перестает быть переходом первого рода и становится непрерывным. Наконец, на рис. 5 показан предельный случай, когда сразу происходит переход из изотропной фазы в смектическую, минуя нематическую. Итак, различия в фазовых переходах на рис. 2–5 объясняются различиями в соотношениях между аппроксимационными коэффициентами для эффективного межмолекулярного потенциала.

Заключение

В данной работе было показано, что переход из нематической фазы в смектическую можно описать в рамках единой теории среднего поля. В отличие от предыдущих подходов, симметрия потенциала задается строго в соответствии с симметрией молекул ЖК. Описаны различные сценарии эволюции молекулярной системы при изменении температуры. Показано, что переход из нематической фазы в смектическую может быть переходом первого рода или непрерывным переходом, а также может отсутствовать вовсе. Тип поведения молекулярной системы определяется исключительно симметрией межмолекулярного потенциала. Для установления степени проявления различных симметрийных особенностей взаимодействия молекул, эффективный межмолекулярный потенциал был аппроксимирован сферическими инвариантами. В результате, в самосогласованные уравнения среднего поля вошли несколько параметров, имеющих прозрачный геометрический смысл.

Работа выполнена при поддержке гранта РФФИ 08-03-90009 и гранта Миннауки MK-2004.2008.2.