Теория резонансного метода определения комплексного модуля сдвига жидкости

Существует множество методов исследования сдвиговых вязкоупругих свойств жидкостей [1]. Однако наибольшее распространение получили резонансные методы. Рассматриваемый в данной работе акустический резонансный метод впервые был реализован в работе [2]. В методе использован пьезокварц Х -18.5 ⁰ среза, имеющий коэффициент Пуассона, равный нулю, что позволяет исследуемой жидкости, находящейся между пьезокварцем и твердой накладкой, испытывать чисто сдвиговые деформации. Взаимодействие пьезокварца с накладкой через прослойку жидкости ведет к изменению параметров резонансной кривой пьезокварца. Возрастание резонансной частоты колебательной системы относительно ненагруженного пьезокварца доказывает наличие сдвиговой упругости у испытуемой жидкости.

В работе [2] измерения проведены при малых толщинах жидкой прослойки, при этом сдвиги частот пропорциональны обратной толщине прослойки жидкости. При увеличении толщины слоя в широких пределах наблюдаются затухающие колебания сдвигов частот. По максимумам затухания определяется длина сдвиговой волны.

• 1    Общее решение задачи взаимодействия колебательной системы пьезокварц — прослойка жидкости — накладка

Влияние добавочной связи на резонансные характеристики колебательной системы будет выражаться в изменении резонансной частоты пьезокварца и затухания, т. е. в изменении волнового числа пьезокварца. Изменение волнового числа определяется приравниванием импеданса жидкости и импеданса пьезокварца.

Импеданс жидкости Z ж равен отношению силы F₀ , действующей со стороны жидкости на пьезокварц, к скорости частиц жидкости V 0 на поверхности пьезокварца. Сила F ₀ равна [3-6]:

_ * ^d^ ⁽ z , t ), ^F 0 = SG —;—I z = 0 -

д^( z , t )

где ——- — градиент смещения частиц жидкости у поверхности пьезо- кварца, S — площадь контакта, G — комплексный модуль сдвига жидкости.

Решая волновое уравнение:

d ² ^ ( z , t )     * d ² ^ ( z , t )

P----5--- = G -----5--- , dt2             dz2

где p — плотность жидкости, можно определить смещение частиц жидкости ^ как функцию времени t и расстояния z от поверхности пьезокварца. Смещение частиц жидкости будет выражаться как суперпозиция прямой и обратной волны:

*              *

5 ( z , t ) = A ( e     + a e - ■ ^z ) e - " ,                      (3)

*

где x — комплексное волновое число жидкости, ю — циклическая частота пьезокварца. A и a — постоянные, зависящие от граничных условий.

Для определения постоянной a рассмотрено взаимодействие прослойки жидкости с накладкой [3-5]. Сила FH, действующая со стороны жид кости на накладку массы т, сообщает ей ускорение

д

—у z = Н , тогда ∂ t

^FH ⁼

_- s _G * ^d^ ⁽ z , t )

I

д Л z , t )

=m dtг

z = H

При решении последнего уравнения относительно a получается:

a=

zm ^ - mx H _ikH

* e imж - mχ H

где т ж — масса жидкой прослойки.

Подставляя (5) в (3) для смещения частиц, получаем:

* *

ξ ( z , t ) = A ( e i χ z + im ж - m χ * H e 2 i χ ^* H e - i χ ^* z ) e - i ω t .             (6)

im_ж + m χ ^* H

Скорость частиц жидкости V ₀ у поверхности пьезокварца находится дифференцированием смещения частиц по времени при z = 0 , т. е.

_V = d ε ( z , t ) I ⁰         ∂ t      ¹ z = 0 .

Следовательно, импеданс жидкости будет иметь вид [4–6]:

* ∂ξ ( z , t )

SG

Z = ^{F 0} ж V ₀

∂ξ ( z , t ) ∂ t

z = 0

^, I z = 0

или, подставляя выражение для чить следующее выражение:

ξ ( z , t ) по формуле (6) в (7), можно полу-

Zж

-

m_ж ω i χ ^* H

m χ H tg( χ H + arctg ).

mж

Импеданс пьезокварца Zк равен отношению силы Ф0 , действующей со стороны пьезокварца на жидкость, к скорости элементов пьезокварца q0 в месте его контакта с жидкостью [3–6]. Смещение элементов пьезок- варца выражается в виде:

U ( x , t ) = U ₀ sin kxe - ⁱ ω ^t ,                            (9)

где k — волновое число пьезокварца.

Сила Ф ₀ равна:

∂ U

Ф ₀ = E ⋅    -1 ⋅ Q = U ₀ ⋅ E ⋅ kQ cos kle - ⁱ ω ^t ,               (10)

∂x x=l где E — модуль Юнга, Q — поперечное сечение пьезокварца, l — по-

= ρ ^E _к

, где с _к —

ловина его длины. Используя выражения k = ω и ск ск скорость продольных волн в пьезокварце, ρк — его плотность, для Ф0 можно получить следующее выражение:

Ф ₀ = U ₀ Q ωρ _кc_к cos kle - ⁱ ω ^t .                    (11)

Скорость элементов пьезокварца на его конце определяется дифференцированием (9) по времени при x = l и имеет вид:

q ₀ = - U ₀ i ω sin kle - ⁱ ω ^t .                       (12)

Таким образом, для импеданса пьезокварца Z_к получим выражение [3–6]:

Ф

Z_к = ⁰ = ic_кQ ρ _к ctg kl .                        (13)

q ₀

Поскольку при взаимодействии пьезокварца с прослойкой жидкости и накладкой изменяется как резонансная частота, так и его затухание, то волновое число пьезокварца становится комплексным. Учитывая это, равенство импедансов жидкости и пьезокварца запишется в виде:

*

im ω           m χ H

_* ^ж tg( χ ^* H + arctg       ) = ic_кQ ρ _к ctg k ^* l .           (14)

χ ^* H             ^mж

Комплексное волновое число пьезокварца приводит к изменению фазы колебания ε , т. е. должно выполняться равенство:

π

.

k l-ε =

Выразив ε через комплексный сдвиг частоты пьезокварца

Δ ω

ε = l , получим: с_к

π Δ ω k l = + l .

• 2     c к

Подставляя это выражение в (14), для комплексного сдвига резонансной частоты Δ ω можно получить следующее выражение:

Δ ω

-

*

2m ω          mχ H ж tg(χ H + arctg ),

M χ H          ^mж

где M = 2 lQ ρ _к — масса пьезокварца. Выражение (17) можно привести к более простому виду [3–7]:

* 2 SG ^* χ ^* 1 + cos(2 χ ^* H - ϕ ^*)

Δ ω =                            ,                 (18)

^M ω   sin(2 χ ^* H - ϕ ^*)

*

где ϕ = ϕ ′ + i ϕ " — комплексный сдвиг фазы при отражении вязкоупругой волны от границы жидкость — накладка.

Используя формулы для комплексного модуля сдвиговой упругости ωρ                             _*

G = и комплексного волнового числа жидкости χ = β - i a , где ( χ ^*)²

β — действительная часть, a — мнимая часть, выражение (18) можно разделить на действительную и мнимую части [3–5; 7]:

2 S ( G ′ β + G " a )sin(2 β H - ϕ ′ ) + ( G ′ a - G " β )sh(2 a H + ϕ ") Δ ω =

Mω

ch(2 a H + ϕ ") - cos(2 β H - ϕ ′ )

, (19)

_{Д а} „ = 2 5 ( G " в - G' a )sin(2 в Н - ф ' ) + ( G " а + G' в )sh(2 а H + ф ")

M a          ch(2 a H + ф") - cos(2 в Н - ф")

Компоненты комплексного сдвига фазы будут иметь следующий вид

[3-5; 7]:

ф ' = arctg       2 в      ,                        (21) m X * |   5р - Sρ    m 2а ф " = arctg------------.                         (22) m X * + 5р

Sρ    m

Действительная часть комплексного сдвига фазы (21) равна разности фаз между прямой и отраженной волнами, мнимая часть (22) характеризует добавочное затухание, которое обусловлено потерей части энергии волны, передаваемой накладке.

При условии, что масса накладки достаточно велика и ее можно считать практически покоящейся, выражения (19) и (20) значительно упрощаются. Так, в формуле (21) вторым членом знаменателя можно пренеб-m\X *2| речь и член —!---1 >> 2в и 2a. Следовательно, при отражении волны от

Sρ границы жидкость — накладка сдвиг фазы не происходит (ф = 0), что означает полное отражение энергии волны.

В случае, когда накладка неподвижна, формулы (19) и (20) принимают следующий вид [3-5; 7]:

_да = 2 5 ( G'в + G" a )sin2 в Н + ( G'а - G " в )sh2 a H

M a          ch2 a H - cos 2 в Н

_Дю „ = 2 5 ( G " в - G 'a )sin 2 в Н + ( G" a + G 'вWall M a         ch2 a H - cos 2 в Н

По выражениям (23) и (24) видно, что при данных свойствах жидкости действительный и мнимый сдвиги частоты являются функциями толщины прослойки. С увеличением толщины прослойки наблюдаются затухающие осцилляции Да' и Да".

Пьезокварц закрепляется по средней узловой линии и состоит из двух равноправных частей с одинаковыми накладками и прослойкой жидкости на обоих концах, поэтому при выводе выражений (23), (24) рассматривалась половина пьезокварца. Обычно в эксперименте жидкость с накладкой находится только на одном конце, тогда в формулах коэффициент 2 пропадает. В данном случае получены следующие выражения для действительного и мнимого сдвигов резонансной частоты:

S   ( G ' β + G " a )sin2 β H + ( G ' a - G " β )sh2 a H

⋅

4 π ² Mf ₀          ch2 a H - cos2 β H

S    ( G " β - G ' a )sin2 β H + ( G " a + G ' β )sh2 a H

⋅

4 π ² Mf ₀           ch2 a H - cos2 β H

Положения максимума затухания найдем приравниванием к нулю производных по толщине от мнимого сдвига частоты (24):

λ H = n .

Таким образом, при толщине прослойки, равной λ, будет наблюдаться первый максимум затухания.

По формулам (25) и (26) рассчитаны теоретические зависимости сдвигов частот от толщины жидкой прослойки при модуле сдвига, равном G = 0.3 ⋅ 10 ⁵ Па , и тангенсе угла механических потерь tg θ = 0.3 (рис. 1).

Из рисунка видно, что зависимости действительного Δ f ' и мнимого Δ f " сдвигов частот от толщины прослойки H действительно дают затухающие осцилляции. При этом при равной толщине жидкой прослойки наблюдается первый максимум затухания.

Af, Гц

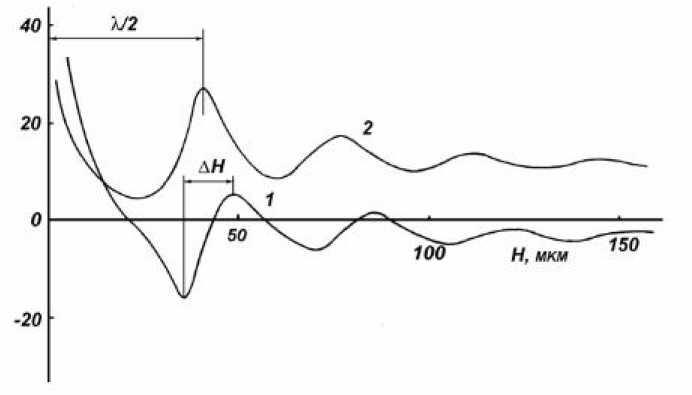
Рис. 1. Затухающие осцилляции сдвигов частоты от толщины прослойки H : 1 – Δ f ' ; 2 – Δ f "

2 Расчет вязкоупругих параметров жидкостей по длине сдвиговой волны

Из рис. 1 и по выражениям (26) и (27) следует, что по экспериментально найденным максимумам затухания колебательной системы можно определить длину сдвиговой волны.

Расчетную формулу для определения G′ получим, рассматривая сле- дующее выражение:

( χ ^*) ² = ωρ , G ^*

*

*

где χ = β - ia — комплексное волновое число, G = G′ + iG" — комплексный модуль сдвига. Подставив эти значения в соотношение (28) и a    θ учитывая, что = tg и tgθ =   , получим, что [3–5]

β    2

β ² (1 - tg ² θ - 2tg θ tg θ ) = ω ρ ,

22 G или

β2 = ω2ρ′ cosθcos2 θ.

2 π

Принимая β =   и переходя к линейной частоте, получим расчетную

λ формулу для определения G′ [4; 5; 7; 8]:

G ′= λ ² f ² ρ cos θ cos² θ ,                      (30)

где λ — длина сдвиговой волны в исследуемой жидкости, f — резонансная частота пьезокварца, ρ — плотность исследуемой жидкости, θ — угол механических потерь.

Измерив расстояние между первым положением максимума и первым положением минимума, можно определить θ [4; 5; 7; 8]. Уравнение (23) показывает, что абсциссы экстремальных точек действительного сдвига частоты находятся из выражения:

cos 2βHch2aH - 1 = 0 .(31)

Из рис. 1 видно, что экстремальные точки действительного сдвига находятся по обе стороны от максимума затухания. Поэтому условия первых экстремумов можно представить в виде:

1-cos(2π- x)ch[tgθ(2π- x)] =0,(32)

1-cos(2π+y)ch[tgθ(2π+y)]=0.(33)

Из этих выражений можно видеть, что положения максимума и минимума являются только лишь функциями тангенса угла механических потерь. В приведенных выражениях получим x+ y = 2βΔH , (34)

где Δ H — расстояние между соседними экстремальными точками действительного сдвига частоты (рис. 1). Из этого следует, что существует определенная корреляция tg θ со значением β Δ H . На рисунке 2 показана

Δ H рассчитанная зависимость tg θ от величины . λ

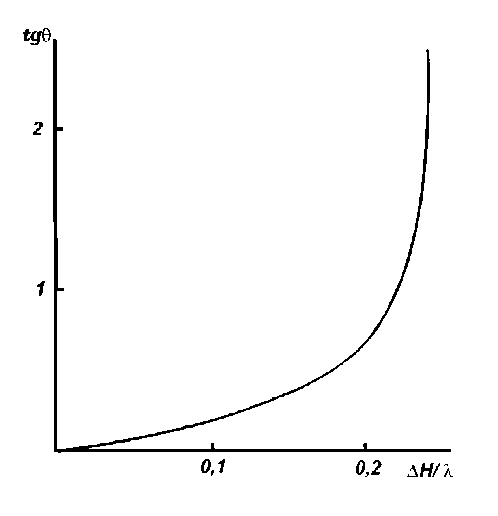
Рис. 2. Зависимость tg θ от Δ ^H λ

Таким образом, для измерения действительного модуля сдвига жидкостей G′ достаточно определить длину сдвиговой волны и тангенс угла механических потерь.

В наших работах [7–12] измерены низкочастотные ( 105Гц) модули сдвига ряда жидкостей. В зависимости от толщины жидкой прослойки H экспериментально получены осцилляции действительного Δf ' и мнимого Δf " сдвигов частот. Длины сдвиговых волн λ определены по мак- симумам затухания. Тангенс угла механических потерь определен по кри- вой зависимости tgθ от H (рис. 2). По выражению (30) рассчитаны λ значения действительного модуля сдвига G′ .

Так для исследованной жидкости ПМС-100 получены значения модуля сдвига и тангенса угла механических потерь [8]. Эти значения равны соответственно G' = 0.58 - 10 5 Па , tg # = 0.5 и совпадают со значениями параметров, полученных другими методами.

Заключение

В данной работе рассмотрено решение задачи взаимодействия колеблющегося на резонансной частоте пьезокварца с прослойкой жидкости, накрытой твердой накладкой. Из решения данной задачи получен способ определения действительного модуля сдвига и угла механических потерь по экспериментально найденной длине сдвиговой волны в полимерной жидкости ПМС-100, рассчитаны вязкоупругие параметры данной жидкости. Хорошее согласие результатов измерения разными способами показало, что данная полимерная жидкость обладает низкочастотной сдвиговой упругостью.