Термодинамическое описание диэлектрической релаксации в граничных слоях жидкости

Исследование кинетики диэлектрической релаксации в граничных слоях полярных жидкостей представляет собой одну из фундаментальных проблем современной теплофизики и физики конденсированного состояния. Формирование граничного слоя с аномальными, по сравнению с объемной фазой, свойствами обусловлено влиянием межфазной границы, заключающимся в существенной модификации межмолекулярных взаимодействий. В приграничной области наблюдается изменение пространственной конфигурации и энергии водородных связей, существенное ограничение конформационной и трансляционной подвижности молекул, а также возникновение статических анизотропных электрических полей. Совокупность перечисленных факторов приводит к установлению ориентационного порядка и возрастанию пространственной корреляции дипольных моментов. Возникающее структурное упорядочение обусловливает модификацию энергетического спектра релаксационных переходов, что выражается в увеличении энергии активации процессов ориентационной поляризации и, как следствие, в смещении характерных времен диэлектрической релаксации. Данные изменения микроскопической динамики проявляются на макроскопическом уровне в отклонении диэлектрической проницаемости и ее дисперсии от объемных значений, а также в поправках к термодинамическим потенциалам граничного слоя.

Современные экспериментальные методы, включая широкополосную диэлектрическую спектроскопию, терагерцевую и инфракрасную спектроскопию, нелинейную спектроскопию генерации суммарной частоты (SFG), а также моделирование методом молекулярной динамики, позволили установить ряд фундаментальных закономерностей. Вблизи межфазных границ наблюдается существенное замедление релаксации, увеличение времени корреляции дипольных флуктуаций и рост эффективной энергии активации [1, 2]. Эти эффекты проявляются даже при толщинах слоя, превышающих несколько нанометров, что указывает на дальнодействующее влияние поверхности и изменение структуры водородной сети на масштабах, значительно превосходящих размеры одной молекулы [3].

Экспериментальные данные о структуре приповерхностных слоев полярных жидкостей свидетельствуют о существенной модификации межмолекулярных взаимодействий вблизи границы раздела фаз. В приграничной области формируются ансамбли молекул с выраженным ориентационным порядком, что свидетельствует о возникновении ориентационной анизотропии и приводит к повышению плотности и устойчивости сети водородных связей по сравнению с объемной фазой [4].

Упорядочение дипольной структуры сопровождается подавлением флуктуаций ориентационного параметра порядка и возрастанием пространственной корреляции ориентаций соседних молекул. Это структурное изменение вызывает модификацию энергетического спектра релаксационных переходов, которая проявляется в увеличении высоты потенциальных барьеров между устойчивыми дипольными конфигурациями. Вследствие этого вероятность термически активируемых перестроек данных конфигураций существенно снижается.

Макроскопическим следствием данного микроскопического механизма является изменение диэлектрических свойств системы, а именно уменьшение скорости диэлектрической релаксации и соответствующее возрастание характерного времени релаксации. Согласно результатам молекулярно-динамического моделирования [5], толщина слоя с аномальными релаксационными характеристиками составляет 2–5 нм и зависит от температуры, химической природы поверхности и ее гидрофильности.

С термодинамической точки зрения релаксационное поведение жидкости вблизи межфазной границы не может быть описано исключительно локальными структурными параметрами, а требует учета вклада избыточной поверхностной энергии в полный термодинамический потенциал системы. Данный вклад существенно меняет условия равновесия между различными метастабильными состояниями дипольных ансамблей, смещая баланс в сторону конфигураций с минимальной поверхностной энергией. Модель, трактующая релаксацию как переход между двумя устойчивыми состояниями, эффективная 88

свободная энергия активации такого перехода, должна включать поправку, обусловленную энергией межфазных границ. В первом приближении для плоской границы раздела величина этой поправки пропорциональна произведению межфазного натяжения на характерный размер области перестройки, которым может служить толщина релаксационного слоя.

Следовательно, релаксационная кинетика в приповерхностной области представляет собой термически активируемый процесс. Его энергетический барьер складывается из двух частей. Первая определяется фундаментальными параметрами среды (температурой и потенциалом межмолекулярного взаимодействия), а вторая представляет собой аддитивную поправку, детерминированную избыточной свободной энергией межфазной границы.

Современная теория диэлектрической релаксации демонстрирует принципиальную неполноту при описании систем с развитой межфазной границей. Классические релаксационные модели (Дебая, Коула-Коула, Гавриляка - Негами), сформулированные для статистически однородных объемных сред, не включают в свои структурные уравнения параметры, характеризующие межфазную границу. Отсутствие в формализме этих моделей таких величин, как межфазное натяжение и толщина переходного слоя, делает невозможным их последовательное применение к описанию тонкопленочных систем.

Экстраполяция указанных моделей на случай тонких пленок приводит к возникновению эмпирических зависимостей, не имеющих строгого физического обоснования. С другой стороны, методы молекулярной динамики и ab initio расчеты, обеспечивая детальную информацию о микродинамике молекул, в силу фундаментальных ограничений по пространственно-временным масштабам не позволяют получить универсальные термодинамические соотношения, необходимые для количественного обобщения экспериментальных данных.

Таким образом, разработка последовательного теоретического формализма, устанавливающего однозначную связь между макроскопическими параметрами диэлектрической релаксации, величиной поверхностной энергии и термодинамическими функциями граничного слоя, представляет собой актуальную фундаментальную проблему физики конденсированного состояния.

Целью данной работы является развитие термодинамического подхода к описанию особенностей диэлектрической релаксации в граничных слоях жидкости. Подход основан на прямом учете энергии межфазных границ через введение соответствующих поправок в потенциал Гельмгольца, что позволяет получить явные выражения для энергии активации и характерного времени релаксации через основные параметры системы (температуру, поверхностную энергию, плотность, толщину граничного слоя) и обеспечить физически прозрачную интерпретацию Аррениусовской кинетики [6].

Материалы и методы исследования

В рамках теории абсолютных скоростей реакций Эйринга процесс диэлектрической релаксации интерпретируется как термоактивированный переход системы через энергетический барьер между двумя локальными состояниями, соответствующими различным ориентационным конфигурациям дипольных групп. Скорость такого перехода определяется выражением [6]:

kT v = ^exP

a g 1 RT J ^,

где A G - изменение свободной энергии Гиббса между исходным и переходным состоянием.

Выбор термодинамического потенциала, описывающего процесс активации, определяется внешними условиями. Для объемных жидкостей релаксация протекает при практически постоянном давлении, поэтому естественным потенциалом служит свободная энергия Гиббса G(T, p). В граничной же жидкости, где молекулы находятся под действием поверхностного потенциала и ограничены в движении, релаксационные акты происходят при постоянных значениях температуры и объеме. При этом работа против внешнего давления отсутствует, и релаксация протекает в условиях, близких к изохорным процессам. Вследствие этого корректным термодинамическим потенциалом для описания переходного состояния является свободная энергия Гельмгольца:

F = U - TS ,                                (2)

где U – внутренняя энергия системы; S – энтропия; T – температура.

Микроскопические перестройки структуры жидкости происходят значительно быстрее, чем наблюдаемая релаксация поляризации, поэтому процесс можно рассматривать как квазистатический. Система успевает устанавливать локальное квазиравновесие на каждом этапе, и ее эволюцию можно описывать как медленное движение по поверхности свободной энергии. В этих условиях каждый акт переориентации диполя или локальной группировки молекул происходит в приближении термодинамического квазирaвновесия. Переход из одного метастабильного состояния в другое осуществляется через переходное состояние (потенциальный барьер F ts ) с минимально возможным изменением потенциала Гельмгольца. Следовательно, диэлектрическая релаксация в граничной жидкости может рассматриваться как квазистатический переход между локальными метастабильными состояниями с близкими значениями потенциала Гельмгольца

F = F 2 .                                       (3)

Энергия активации релаксационного процесса  AF  определяется высотой потенциального барьера

A F = F ts - F 1 = F ts - F 2 .                                 (4)

В рамках квазистатического приближения свободная энергия Гельмгольца граничного слоя жидкости F i может быть представлена в виде суммы двух независимых вкладов – объемного U - TS и граничного c A ( ст - удельная энергия межфазных границ, А - площадь межфазных границ). Такое аддитивное разложение имеет твердое физическое обоснование и широко используется в теории поверхностных явлений и жидкостей в ограниченном пространстве. Прежде всего объемный вклад U – TS определяется локальными межмолекулярными взаимодействиями в жидкости (водородными связями, дисперсионными силами, энтропией ориентационных степеней свободы) и практически не зависит от присутствия границы на расстояниях, превышающих характерную длину корреляции (обычно 0,5-3 нм для полярных жидкостей). Межфазный вклад c A возникает вследствие дополнительного потенциала взаимодействия молекул с твердой поверхностью и экспоненциально затухает при удалении от границы. Вследствие различия пространственных масштабов эти два вклада слабо пересекаются, что позволяет их суммировать независимо.

Свободную энергию активации Гельмгольца для граничной жидкости запишем как

A F = U ts - TS s + c _sA - U 1 + TS₁ -c 1 A = A U - T A S + Ac A .           (5)

Стандартная кинетическая запись для времени релаксации в форме Эйринга имеет вид:

т = — exp kT

A F

RT

.

С учетом энергии межфазных границ время диэлектрической релаксации в граничной жидкости

h

т, = —exp i kT

A U - T Л S + Ao A

RT

Для анализа зависимости межфазного вклада от толщины граничного слоя запишем энергию активации единицы объема жидкости

A f = A u - T A s + Ag- ,

J                      v , где u - удельная внутренняя энергия единицы объема жидкости; s - плотность энтропии; о -энергия межфазных границ; A - площадь межфазных границ; V- объем жидкости в граничном слое; 1/d = A/ V- толщина граничного слоя.

Переходя от удельных величин к энергии на моль вещества A F , представим энергию активации релаксационного процесса в виде следующего выражения:

A F = |Д u - T A s + —|^Р , I            d J Р

где р - молярная масса; р - плотность граничной жидкости.

С учетом геометрических и термодинамических параметров граничного слоя это приводит к окончательному выражению для времени диэлектрической релаксации:

h

т, = — exp i _kT

—| A u - T A s + — р RT <          d

Следовательно, время релаксации в граничном слое определяется температурой, толщиной слоя и изменением поверхностной энергии при переходе системы из возмущенного в равновесное состояние. Экспоненциальная зависимость (10) объясняет увеличение времени релаксации по мере роста энергетического вклада межфазных границ и уменьшения толщины слоя.

В случае жидкого слоя на твердой подложке необходимо учесть вклад двух межфазных границ: «твердое тело - жидкость» Ao s и «жидкость - пар» Ao i . Поскольку их энергии аддитивны, выражение (10) обобщается до вида

h т, = —exp i kT

-^| A u - T A s + _р RT ^

Ao s + Ao l d

Результаты исследования и их обсуждение

Полученные уравнения энергии активации и времени релаксации описывают влияние поверхностных эффектов и геометрических ограничений на динамику дипольных перестроек в граничной жидкости. Выражение для энергии активации (9) отражает термодинамическое равновесие между внутренней энергией слоя и поверхностной энергией межфазных границ. При уменьшении толщины слоя ( d ) растет относительный вклад поверхностных энергий о s и о f , что приводит к увеличению энергетического барьера релаксации.

Экспоненциальная зависимость времени релаксации (10) выведена в рамках теории абсолютных скоростей реакций Эйринга и отражает кинетическую природу релаксационного перехода как активационного процесса. Можно сказать, что параметр τ0, в отличие от модели Дебая, имеет физический смысл элементарного времени поворота дипольного момента ансамбля молекул, характеризующего частоту индивидуальных попыток преодоления энергетического барьера. При этом энергия активации Ei в граничной жидкости включает не только вклад межмолекулярных взаимодействий, связанных с ориентационными перестройками диполей, но и дополнительную работу, необходимую для изменения локального (флуктуационного) объема [7]. Последний параметр отражает коллективный характер релаксации: перестройка ориентационного состояния не ограничивается вращением одной молекулы, а представляет собой согласованное движение целого ансамбля диполей, взаимодействующих через водородные связи и электростатические силы. Такое кооперативное смещение сопровождается изменением локальной плотности и давления, т. е. требует дополнительной энергии на деформацию микроскопического объема жидкости. В этом смысле энергия активации Ei характеризует не только барьер межмолекулярного взаимодействия, но и работу, совершаемую системой при создании флуктуационного объема, необходимого для коллективного перехода.

Следует отметить, что данный подход применим при сравнительно малых толщинах слоя (до 15 нм), когда система сохраняет непрерывность структуры, но уже испытывает заметное влияние поверхности. При больших толщинах эффект поверхностной энергии ослабевает, и релаксация описывается обычной дебаевской зависимостью.

Таким образом, полученные выражения объединяют термодинамический и структурно-флуктуационный подходы, связывая макроскопические релаксационные характеристики с микроскопическими параметрами межмолекулярных взаимодействий и поверхностной энергии. Это обеспечивает физически наглядную интерпретацию экспериментальных зависимостей τ( d ) и задает основу для описания других систем с ограниченной геометрией - от гидратированных биомембран до нанопористых материалов.

Для проверки предложенного термодинамического описания диэлектрической релаксации в граничных слоях была проведена серия измерений комплексной диэлектрической проницаемости адсорбированной воды при различных толщинах слоя. Исследование выполнено акустоэлектрическим методом [8] в диапазоне частот 2·10⁷ – 4·10⁸ Гц и при температуре 293 K. Геометрические параметры подложки и их предварительная очистка пламенем водородной горелки обеспечивали воспроизводимое формирование полимолекулярного слоя воды. Толщину адсорбционного слоя задавали посредством регулирования относительной влажности и времени адсорбции молекул воды на предварительно подготовленную гидрофильную поверхность подложки LiNbO 3 YZ -среза.

Полученные спектры диэлектрической проницаемости ε′ ( ω ) и ε″ ( ω ) для различных значений толщины ( d ) представлены на рисунке 1. Для всех исследованных толщин наблюдается выраженная релаксационная мода дебаевского типа. При уменьшении толщины слоя положение максимума поглощения ω m заметно смещается в низкочастотную область. Такое поведение спектров ε′ ( ω ) и ε″ ( ω ) свидетельствует об увеличении характерного времени диэлектрической релаксации по мере усиления влияния межфазной границы.

Количественный анализ спектров осуществлялся путем аппроксимации экспериментальных данных функцией Дебая. Для каждого значения толщины адсорбционного слоя d определялись параметры: статическая диэлектрическая проницаемость ε s , высокочастотный предел ε ∞ и время релаксации τ .

На рисунке 2 показана зависимость времени диэлектрической релаксации от толщины слоя τ ( d ), демонстрирующая экспоненциальный рост времени релаксации при уменьшении толщины слоя ниже 5–7 нм. Это полностью согласуется с предположением о значительном вкладе поверхностной энергии в формирование энергетического барьера релаксационного перехода.

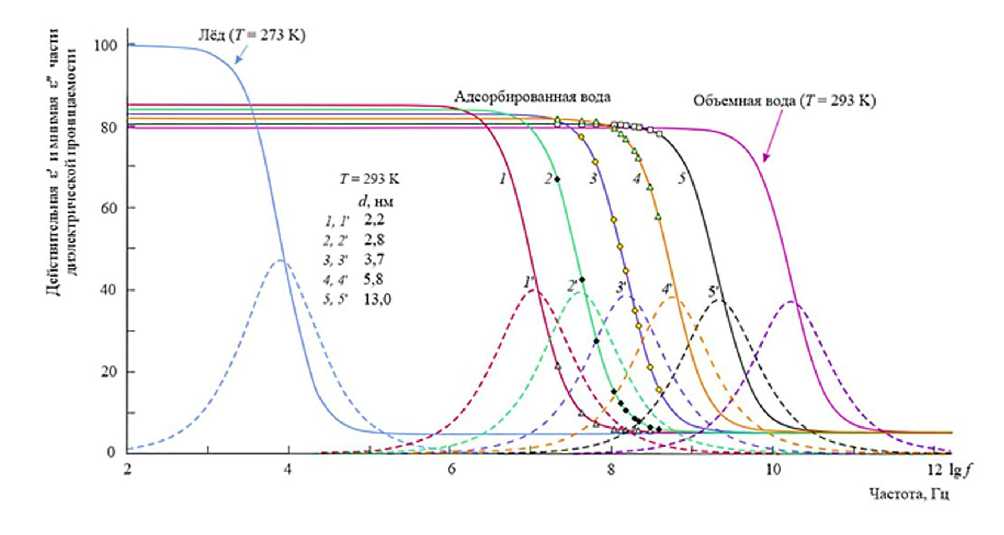
Рисунок 1 – Диэлектрический спектр адсорбированной воды

Отдельно следует отметить, что для больших толщин ( d ≥ 10 нм) значение времени релаксации τ приближается к величине, характерной для объемной воды. Это указывает на локализованный характер влияния межфазной границы «твердое тело – жидкость» и согласуется с молекулярно-динамическими расчетами структуры приповерхностного слоя [9].

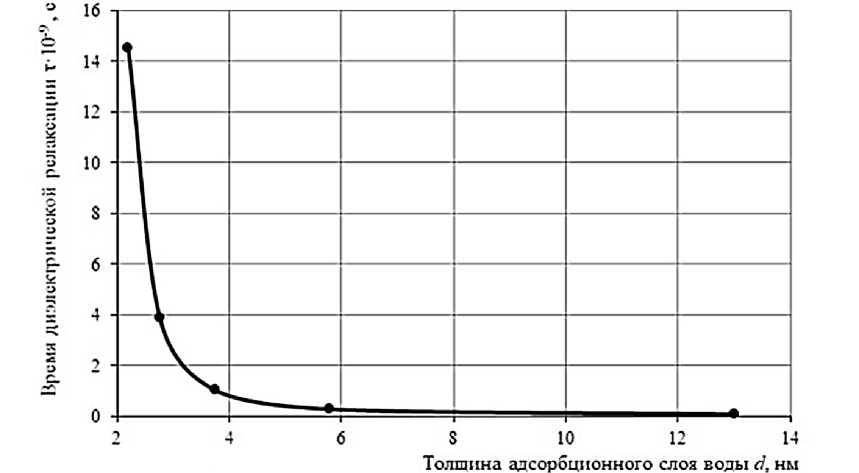
Рисунок 2 – Зависимость времени диэлектрической релаксации в адсорбированной воде от толщины слоя

Заключение

Предложенный термодинамический подход к описанию диэлектрической релаксации в граничных слоях жидкости формирует связное представление о влиянии межфазной энергии и геометрических ограничений на энергетический барьер и характерное время 93

релаксационного процесса. Вместе с тем предложенный подход обладает рядом ограничений, определяющих границы ее применимости и требующих дальнейшего теоретического и экспериментального уточнения.

Во-первых, подход основан на квазистатическом приближении, предполагающем равновесный характер перехода между локальными ориентационными состояниями. Это допущение оправдано для тонких слоев с подавленными флуктуациями объема, однако может быть нарушено при высоких температурных градиентах, воздействии внешних полей или в условиях интенсивного массопереноса. В таких режимах существенную роль могут играть неравновесные динамические механизмы, которые в рамках данного подхода не учитываются.

Во-вторых, линейная зависимость поверхностного вклада от толщины слоя, положенная в основу подхода, является приближенной. Она корректна для плоских, геометрически однородных границ, однако в реальных структурах значимыми факторами являются кривизна, наношероховатость, вариации локальной гидрофильности и доменные неоднородности. Эти факторы приводят к пространственной модуляции значений межфазной энергии, что может существенно изменить величину термодинамической поправки, определяющей эффективный энергетический барьер.

В-третьих, данный подход предполагает, что система обладает только одним характерным временем релаксации. Однако в реальности в неоднородных граничных слоях может присутствовать целый набор релаксационных времен, отражающий сложность локальных структур и различие их динамики. Кроме того, подход не учитывает возможные нелинейные эффекты – например, связанные с сильной поляризацией, нестабильностью сетки водородных связей или локальными микроскопическими перестройками в адсорбционных слоях. Поэтому применение данного подхода корректно лишь в тех случаях, когда диэлектрическая релаксация описывается уравнениями Дебая с одним доминирующим временем релаксации.

Практическая реализация данного подхода также связана с рядом трудностей. Во-первых, определение толщины адсорбционного слоя и его термодинамических параметров с достаточной точностью требует применения независимых методов, что усложняет экспериментальные измерения и повышает требования к воспроизводимости условий эксперимента. Во-вторых, значения межфазных энергий зачастую доступны только опосредованно, через результаты молекулярно-динамического моделирования или косвенных экспериментов, что затрудняет оценку энергии активации. Наконец, подход чувствителен к внешним параметрам – температуре, влажности, состоянию поверхности подложки, – что требует строгого контроля экспериментальных условий.

Несмотря на указанные ограничения, предложенный подход демонстрирует качественное соответствие с экспериментальными результатами и обеспечивает физически обоснованную интерпретацию зависимости времени релаксации от толщины слоя. Дальнейшее развитие предложенного подхода предполагает уточнение связи между кооперативной динамикой дипольных ансамблей и поверхностными эффектами, а также с расширением формализма на тонкие слои со сложной морфологией межфазных границ и многомодовой структурой релаксационных спектров.