Термодинамика фазового равновесия в системах твердое тело-жидкость и твердое тело-газ

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

На основе уравнения Гиббса и объединенного уравнения I и II законов термодинамики можно записать термодинамические потенциалы: внутренняя энергия U dU = TdS - pdV + MN(2)

энтальпия H dH = TdS + Vdp + 5 Mi dN(3)

свободная энергия Гиббса G dG = - SdT + Vdp + MN(4)

Система равновесна не только, когда все параметры постоянны во времени, но и в том случае, когда нет никаких стационарных потоков за счет действия каких-либо внешних источников. Система выводится из равновесного состояния, если подвести к ней вещество или энергию. При этом перенос массы и энергии в пространстве может происходить как принудительно, так и самопроизвольно. В конечном счете, система приходит в состояние динамического равновесия.

Для изолированной системы характерно постоянство макроскопических параметров вещества во времени и в пространстве. В соответствии со вторым законом термодинамики энтропия изолированной системы стремится к максимуму. В состоянии равновесия энтропия системы имеет максимально возможное для данной системы значение, то есть в равновесной изолированной системе dS = 0 . Действительно, для этой системы dU = 0 и dV = 0 .

Исходя из технической термодинамики для открытой системы равновесное состояние достигается только при ее равновесии с окружающей средой в результате тепло-и массообменного взаимодействия. Вследствие отклонения от равновесия в самой системе или в окружающей среде возникает движущая сила процессов, приводящих к изменению свойств системы. Если внешние условия неизменные, то состояние равновесия удерживается в системе сколь угодно долго.

Состояние устойчивого равновесия (стабильное состояние) характерно тем, что если каким-либо внешним воздействием вывести из него рассматриваемую систему, а затем снять это внешнее воздействие, то система возвратится в исходное состояние равновесия [3].

Устойчивое равновесие достигается при условии минимальных значений внутренней энергии U , энтальпии H и свободной энергии Гиббса G .

Результаты и обсуждение

В [1] отмечено, что для устойчивой системы должно соблюдаться неравенство:

U2G (d N,²

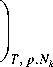
ddi  I l5N JT, P,Nk .1

> 0

Предел существования устойчивой фазы достигается при ( 5 dj 8N )_{r pN} = 0.

Если система находится в состоянии неустойчивого равновесия (лабильное состояние) и из него ее вывести, то система уже не возвратится в исходное состояние, а перейдет в новое состояние устойчивого равновесия. Даже очень малые внешние воздействия выводят систему из лабильного состояния [8–20].

При условии ( d dj 8N; )_TpN^< 0. система неустойчива вследствие возникновения движущей силы для разделения на две равновесные фазы различного состава.

Исходя из условия устойчивости (5) для двухфазной системы запишем:

^T1 = ^T2 ; ^pi = ^p 2 ; M il = M i 2 , ⁽⁶⁾ где индексы 1 и 2 относятся к разным фазам, а T, p и μ – их температуры, давления и химические потенциалы.

Таким образом, если две фазы находятся в равновесии, то температуры, давления и химические потенциалы эти фаз равны между собой. Равенства (6) выражают условия термического и механического равновесия, а также условие отсутствия движущей силы для переноса компонента через границу раздела фаз.

В [1] отмечено, что для однофазной системы уравнение Гиббса-Дюгема имеет вид

ΣX i dμ i = 0 при T и p= const.

При этих условиях для двухфазной системы уравнение принимает вид:

( V ₂ - V ) dp = ( S ₂ - S ) dT + S ( X ,₂ - X , J dM , (7) где V и S – объем и энтропия 1 моля смеси; Х – содержание любого компонента, выраженное в мольных долях.

Рассмотрим экстрагирование из частиц люпина подсырной сывороткой (система твердое тело–жидкость). В определенные моменты процесса может наступить состояние, близкое к равновесию. В условиях равновесия открытой системы концентрация экстрагента в парах приобретает постоянное значение, равное концентрации экстрагента в аппарате.

Запишем иное толкование равновесия: равновесие в рассматриваемой системе наступает тогда, когда химический потенциал растворенного вещества становится равным величине химического потенциала в исходном твердом материале.

Движущей силой процесса экстрагирования в системе твердое тело–жидкость является разность между концентрацией растворяющегося вещества у поверхности твердого тела С и его средней концентрацией С0 в основной массе раствора. Концентрация на границе раздела фаз обычно принимается равной концентрации насыщенного раствора Сн, поскольку вблизи поверхности твердого тела равновесие устанавливается довольно быстро. Тогда движущая сила процесса выражается как разность (Сн-С0). Скорость процесса определяется по уравнению массоотдачи [2].

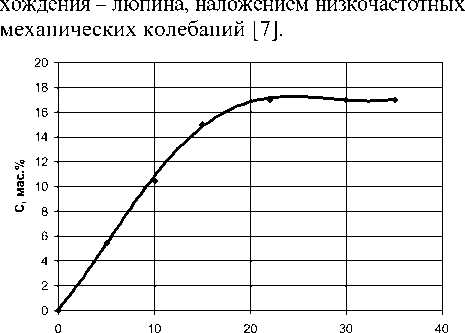
Изложенные выше рассуждения иллюстрируются рисунком 1. Кинетическая кривая, построенная в координатах С(τ) , показывает изменение концентрации экстрагента во времени. В качестве экстрагента использовалась подсырная сыворотка, с целью извлечения целевых компонентов (белков) из сырья растительного проис-

т, мин

Рисунок 1. Кривая кинетики извлечения экстрактивных веществ из люпина подсырной сывороткой наложением низкочастотных механических колебаний: частота колебаний n = 10 кол/с; амплитуда колебаний А = 5,5 мм; температура t = 50 °C; форма тела – крупка

Figure 1. Kinetic curve of extraction of extractive substances from lupine with cheese whey by superimposing low-frequency mechanical vibrations: vibration frequency n = 10 count/s; vibration amplitude A = 5.5 mm; temperature t = 500 °С; body shape – grains

Низкочастотные механические колебания использовались как один из методов интенсификации экстрагирования. Процесс сокращался до 2,5 раз по сравнению с эстрагированием в плотном слое.

Фазовое равновесие в системе твердое тело–жидкость наступало через 18 минут (рисунок 1), то есть в частицах люпина и в подсырной сыворотке концентрации были равными. В данном случае условия устойчивости двухфазной системы выражаются равенствами (6).

Движущей силой процесса конвективной сушки является разность между равновесной и рабочей концентрациями сушильного агента. Она может быть также выражена разностью температур, парциальных давлений или энтальпий паро – газовой смеси в потоке и на поверхности материала.

Как отмечается в [4], вследствие выравнивания концентраций и температур в процессе сушки сила изменяется вдоль сушильного тракта, поэтому при расчете необходимо принимать среднее значение движущей силы Δ или выражать ее через число единиц переноса m .

В период внутреннего испарения температура центра образца материала повышается с течением времени, но немного медленнее, чем температура поверхности материала. Вследствие этого внутри материала возникает температурный градиент. Последний постепенно уменьшается и при достижении равновесного влагосодержания становится равным нулю. В равновесном состояния убыли влагосодержания не происходит, а температура материала равна температуре воздуха.

Движущая сила выражается также как разность парциальных давлений пара над поверхностью материала p м и превышающим его парциальное давление в воздухе или газе p п , то есть при p м > p п.

В процессе сушки параметр p м уменьшается и приближается к пределу p м = p п . При этом наступает термодинамическое равновесие, которому соответствует предельное влагосо-держание материала, то есть равновесное вла-госодержание u р . В свою очередь u р зависит от парциального давления водяного пара над материалом p п или пропорциональной ему параметру относительной влажности воздуха φ .

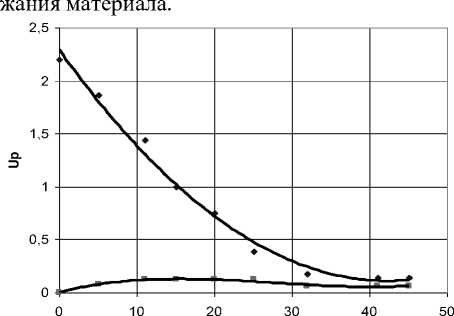
Характер изменения влагосодержаний в процессе сушки представлен на рисунке 2. Здесь G н – удельная нагрузка на опорно-газораспределительную решетку; T гн – температура воздуха начальная; φ н – относительная влажность воздуха; υ – скорость воздуха; u* -критическое влагосодержание, кг воды/кг сухого материала; τ* – продолжительность периода поверхостного испарения (первого периода сушки), мин.

Как показано на рисунке 2, когда влаго-содержание материала, уменьшаясь при сушке, переходит через значение критического влагосо-держания u* (максимального гигроскопического состояния), начинается период внутреннего испарения – период падающей (убывающей) скорости сушки.

Второй период характеризуется тем, что возрастает внутридифффузионное сопротивление, поэтому количество влаги, подводимой к поверхности испарения, уменьшается и интенсивность процесса убывает. Температура материала, изменяясь во времени, непрерывно увеличивается от значения, равного температуре мокрого термометра, до температуры окружающего сушильного агента – при достижении материалом состояния, равновесного с состоянием воздуха. Равновесное состояние влажного воздуха и материала определяется сопряженными значениями относительной влажности воздуха и равновесного влагосодер-

• т, мин

Рисунок 2. Характер изменения влагосодержаний u(τ) и u р (τ) в процессе сушки хлебопекарных дрожжей в псевдоожиженном слое при начальных размерах гранул: диаметр 2 мм, длина 6 мм и параметрах процесса: G н = 45 кг/м ² ; T гн = 40 °С; φ н = 24 %; υ = 2,93 м/с; T н = 20 °С; 1 – u(τ) ; 2 – u р (τ)

Figure 2. The nature of the change in the moisture content u(τ) and u р (τ) during the drying of baker's yeast in a fluidized bed with the initial size of the granules: diameter 2 mm, length 6 mm and process parameters: G н = 45 kg/m²; T g = 400 °C; φ н = 24%; υ = 2.93 m/s; T n = 200 °C; 1 – u(τ); 2 – u р (τ)

При сушке термочувствительных материалов (система твердое тело–воздух) их конечное значение влагосодержания, всегда больше равновесного. В этом случае термодинамика неравновесной системы и ее устойчивость выражаются неравенством:

T * T₂ ; P 1 * p ₂ ; ц _а *^ i2 , (8)

то есть температуры, давление и химические потенциалы фаз не равны между собой, равно как и их градиенты.

Заключение

При достижении экстрагированием фазового равновесия система характеризуется как равновесная и устойчивая. Решается важная технологическая задача: максимальное извлечение из твердого тела целевых компонентов.

При сушке термолабильных материалов система твердое тело–воздух является неравновесной и неустойчивой. Специфика сушки термочувствительных материалов имеет непосредственное отношение к задаче получения необходимых наилучших технологических свойств гороховых продуктов.