The cosmography and cosmology of Wang Chong in the light of Greek and Latin parallels

Wang Chong (27–ca. 102) offers in his extensive work, the Lunheng, a critical examination of a wide variety of views. He discusses particular astronomical theories; he deals with the location of China on the earth's surface; he considers what determines the successes and failures in the careers of ordinary people and rulers, the possibility of predicting the future, physiognomy, the idea of spirits, and a number of other issues. He repeatedly criticizes the views of certain literati. Typically, scholars cannot connect this or that view of Wang Chong’s literati with a particular name or book. We will consider the possibility that some of the views of both the literati and the critic go back to Greek scientific and philosophical, mostly Presocratic traditions.

Wang Chong invokes the following analogy to illustrate the contrary motion of the sun and moon (which they accomplish during a year or a month respectively) relative to the fixed stars:

其喻若蟻行於磑上，日月行遲，天行疾，天持日月轉，故日月實東行 而反西旋也。 (Huang Hui 1990, 11.32/498).¹

“Their movement may be compared to that of ants crawling on a rolling millstone. The movements of the sun and the moon are slow, whereas heaven moves very fast. Heaven carries the sun and the moon along with it, therefore they really move eastward, but are turned westward” (Forke 1962, 266; cf. 267).

Scholars observed that the same analogy is found in Vitruvius:

“Let us suppose that on a wheel such as potters use, seven ants are placed, and as many channels are made in the wheel round the centre as the lowest point, increasing in length to the most distant; let the ants be compelled to make a circuit in these channels and let the wheel be turned the other way; in spite of the revolution of the wheel, they will necessarily complete their journeys in the opposite direction. That which has the channel nearest the centre completes its wandering more quickly; that which traverses the farthest circuit of the wheel, even if it walks as quickly, finishes its course much more slowly on account of the magnitude of the orbit. In like fashion, the planets advancing in a direction opposite to the movement of the firmament complete a circuit along their own paths. Yet in the revolution of the sky they are carried backwards, by the excess of it over their own motion, in the daily circuit of time” (9.1.15; Granger 1934, 225).

Vitruvius illustrates in fact two different ideas at once, the contrary motion of the planets and the effect that some planets “seem to move more swiftly” (9.1.14) than others. Although the potter's wheel fits well for such a combination (one can see in museums examples of ancient potter's wheels with concentric tracks left on the surface), seven ants crawling along seven channels, as in Vitruvius, is a later expansion. All Greek parallel texts (Cleomed. p. 11.17 sqq. Todd; Anon. in Arat. Phaen. p. 97 Maass; Achill. Isag . 20, p. 48 Maass; Procl. In Plat. remp. II p. 234 Kroll) invoke such similes to illustrate only the contrary or double motion of the planets and never the completion of seven revolutions in different times. The text from the commentary on Aratus is convenient to cite because it is neither too short nor too long:

“Heaven moves from the east to the west, while the sun and the other planets in the opposite way, that is to say from the west to the east, so that they have double movement, for they accomplish their own advancement, on the one hand, and are carried, on the other hand, like in the case with the wheel and the ant” (Anon. in Arat., p. 97 Maass).

While the cited author speaks about “the sun and the other planets,” he refers to the ant in singular; moreover, only the sun figures in the ant simile as formulated by Achilles. Now the simile does not illustrate the most intriguing fact about the movement of the planets other than the sun and moon, that is, their apparent stops and their retrograde motion. This let us conclude that the ant simile was introduced earlier than about the middle of the fourth century, when, in the times of Eudoxus and Plato, the retrograde motion of the planets was recognized as a problem of central importance. It seems that the original simile aimed first of all to illustrate the movement of the sun.

The doxographic tradition makes already Alcmaeon (c. 500 BC) “agree with certain mathematicians” that “the planets move from west to east contrary to the movement of the fixed stars” (Dox. 345; 24 A 4 DK). Anaxagoras (his work was known in the late 460-s) and Democritus (who was young when Anaxagoras was old – DL 9. 41) contested this view, but Oenopides (contemporary of Democritus) established it firmly (41 A 7, 10 DK). It is characteristic that all testimonies related to Oenopides' teaching of the two contrary rotations mention exclusively the sun and never the other planets.

Three of the four Greek writers who use the ant simile do not specify what kind of wheel they mean, though Achilles seems to mean the chariot wheel. Cleomedes, however, speaks, in agreement with Vitruvius, about the potter's wheel. But it is easy to conceive how the originally unspecified or invoking a mill-stone comparison could be specified or transformed. As it was explained above, a potter's wheel with tracks left on its surface is very good to illustrate the movement of the seven planets, while the speed with which a potter's wheel rotates is also good to illustrate the fast movement of heaven.² On the other hand, it is rather enigmatic what should bring the ants on a potter's wheel, while everybody would easily grasp what they do on a mill-stone. Thus, it is quite likely that the original Greek simile had the ant(s) on a mill-stone. For the question of transmission of the simile from the Greek world to China, the exact kind of wheel is at any rate of little importance because one can see that minor modifications of the simile took place repeatedly within the Greek tradition itself.

Wang Chong's comparison of the sun and moon to the ants and that of heaven to the mill-stone belongs to a larger whole. There were two most influential traditions in ancient Chinese cosmography. The one, the gai tian , held the view that heaven rotated above the earth; the other, the hun tian , assumed that heaven is a sphere with the earth in the middle of it (Ho Peng Yoke 1966, 49 ff.; Needham 1959, 210–216; Cullen 1977, 81–122; 132 ff.; Cullen 1996). The ant simile belonged to the gai tian . It appears once more in the description of the gai tian / Zhou bi school in the Jinshu :

天旁轉如推磨而左行，日月右行，隨天左轉 …… 譬之於蟻行磨石之 上，磨左旋而蟻右去，磨疾而蟻遲，故不得不隨磨以左迴焉。 (Fan Xuanling et al. 1974, 11/279).

“The heavens rotate sideways towards the left like the turning of a millstone. Both the sun and the moon move towards the right, and at the same time they have to follow the heavens, which rotate towards the left ... This is analogous to an ant crawling on a millstone, such that while the millstone is rotating towards the left, the ant is attempting to move to the right. But the rotation of the millstone is much faster than the movement of the ant. It can be seen that the ant is compelled to follow the motion of the millstone, and that apparently it is moving towards the left” (Ho Peng Yoke 1966, 51; cf. Needham 1959, 213).

The comparison of the heaven's rotation to the turning of a mill-stone seems to have been one of the labels of the gai tian system. The rival system, the hun tian , seems to have had as such the comparison to the rotation of a chariot wheel. It appears in a classic description of the hun tian universe by Zhang Heng (78–139).

There is nothing extraordinary, of course, in choosing a mill-stone and a chariot wheel to illustrate the two different types of rotation. It is worth noting, however, that the same distinction for two different notions is found among the Greeks too. In formulation by Theodoretus, “some assert that cosmos rotates like a mill-stone, the others that it rotates like a wheel” (Dox. Gr. 329, note). Theodoretus lived later than both Wang Chong and Zhang Heng, but his remark goes back to a source composed centuries earlier and through it probably to the work by Theophrastus (late fourth century BC) which was devoted to the opinions of early philosophers.

One more remark seems appropriate. The ant similes imply that the planets and first of all the sun as the main subject of such similes are somehow attached to heaven. For a naïve view, there is nothing to suggest this idea; on the contrary, the sun, moon, Venus and other planets are naturally perceived as independently moving objects. The Presocratic cosmologists held, however, diverging views on the subject. The preserved evidence is scanty and sometimes (as in the case of Anaximander) controversial, but there is still something unambiguous. It is reported about Archelaus' cosmogony: “He says that the heavens are inclined, with the result that the sun gave light on the earth, made the air transparent, and the earth dry” (Kirk, Raven, Schofield 1983, 387; 60 A 4 DK). If Archelaus connected the effects caused by the sun with what had happened to heaven, it follows that he considered the sun in this or that way attached to heaven.

Alfred Forke, while observing the parallelism between the comparisons used in both Vitruvius and Wang Chong calls it "a curious coincidence" (Forke 1925, 13 f., n. b; 32). From his point of view, "any influence of Chinese astronomy on the Greek or vice versa is out of the question of course". Also according to Joseph Needham, "there can be no question of a transmission of the thought" (Needham 1959, 214). However, a coincidence in this case must be regarded as a miracle. Indeed, there are two common ideas behind the analogy, that heaven and the planets move in opposite directions and that the planets (at least the sun and moon) are somehow attached to heaven. Neither of the two is surprising, but the history of astronomy shows that neither is self-suggesting as well. Even less self-suggesting is the ingenious analogy used to illustrate the combination of both ideas. Standard procedure of scholarly interpretation unambiguously suggests a transmission.

Indeed, one finds the same simile also in Cosmology by Armenian polymath of the seventh century Anania Shirakatsi:

“There is no need for us to compare the motion of the luminaries with that of an ant, or with anything else of the kind, as the pagan philosophers who say: the ant may serve you as an example; take the ant and put it on a millstone and see why it moves against the motion of the millstone... And the millstone, owing to its speed, carries it away with it in the direction in which it rotates itself....” (Shirakatsi 1962, 78–79).3

Vitruvius' treatise appeared a hundred years earlier than that of Wang Chong and Vitruvius' ultimate Greek source must have been composed even earlier, probably in the fifth or even late sixth century BC. Thus, there are good reasons to assume a diffusion in the eastward direction.

We address now another statement by Wang Chong:

儒者曰：「天、氣也，故其去人不遠。人有是非，陰為德害，天輒知 之，又輒應之。」 (Huang Hui 1990, 11.31/482).

“The Literati say that heaven is air, and therefore not far from man. Consequently it immediately knows, whether they are right or wrong, and whether they possess secret virtues or vices, and also responds to them” (Forke 1962, 257).

We find the same idea in the Greek world and much earlier than in China. It is most clearly expressed in a passage from a lost comedy of Philemon. This once famous comedian was a native of Syracuse, but became an Athenian citizen. He lived a long life, about a hundred years. His fame came from his victory in a competition of comic poets, which he won in 327 BC. Here is what he says (fr. 91 Kock; 64 C 4 DK):

I'm the one no one can hide from, no matter what they've done, or is about to do or has done in the past, No god, no man,

I am Air, which may be called Zeus.

I am everywhere, and this is the work of god, Here in Athens, in Patras, in Sicily, In all cities, in all houses,

In all of you. There is no place

Where there is no Air, but he who is present everywhere, Necessarily knows everything, since he is present everywhere.

We may agree that air is present in all cities and in all houses. However, very few of us would draw from this a conclusion that air knows everything. Such an idea in no way suggests itself, which makes it quite problematic that this idea could independently arise in both Greece and China. The idea of air endowed with reason and present everywhere was put forward as early as Diogenes of Apollonia. Part of the tradition calls him a disciple of Anaximenes (64 A 1 DK), but Theophrastus saw in his views a dependence on Anaxagoras and Leucippus (64 A 5 DK). For our purposes, it is not of primary importance whether Diogenes' work belongs to the beginning or rather to the middle of the fifth century BC. Symplicius cites Diogenes for the following statement:

“And it is my view that that what possesses cognitive activity ( noêsis ) is what humans call ‘air,’ and that it is by this that all are steered and at the same time dominate over all. For it is my view that it is this itself that is god, and that it arrives everywhere, arranges all things, and exists in every thing” (64 B 5 DK; Laks, Most 2016, 235).

We are also told that “Diogenes praises Homer for his reasoning about deity not mythically, but truly, for according to him, Homer thinks Zeus is air, because he says Zeus knows everything” (64 A 8 DK).

A curious situation emerges. While no Chinese member of the group of the learned people criticized by Wang Chong was ever identified, this group includes Diogenes of Apollonia, an early Greek philosopher.

It is appropriate to add to the point that the very idea of air is in a way a theoretical construction. (Did anybody ever see air?) This was Anaximenes who introduced the idea of omnipresent, pervasive air. He used this term interchangeably with the term pneuma , ‘breath’, which corresponds well to Chinese qi , used by Wang Chong in the discussed passage.

However, one may not speak of transmission in this case as confidently as in the case of the ant on a mill-stone. Since the ascending of the Zhou dynasty there was a firmly established notion in China according to which a ruler receives his Mandate from Heaven ( tian ming 天命 ) and his received right to rule is conditional and can be withdrawn if he displays improper attitude towards his subjects or moral and ritual traditions. Such a notion implies that Heaven is aware of what happens on earth. In V–IV centuries BC this idea was further developed by Mohists, who argued that Heaven watches over not only the ruler, but also ordinary men:

且語言有之曰：『焉而晏日焉而得罪，將惡避逃之？』曰無所避逃 之。夫天不可為林谷幽門無人，明必見之。 (Sun Yiran 2001, 7.26/192–193)

“Moreover, there is the saying: ‘If someone commits a crime in the bright light of day, how will he flee from it?’ – which is to say there is no place to escape to. Now, with Heaven, there cannot be a forest, valley or dark and secluded place that it does not certainly see clearly” (Johnston 2010, 233).

Well before the time of Wang Chong there also appeared a notion according to which heaven is an accumulation of qi . Through combining the specified ideas a Chinese thinker could arrive independently from any Greek one at the insight that heaven, being both capable of knowledge and omnipresent in the capacity of an accumulation of qi , knows everything. It is also worth mentioning that what Wang Chong writes about is not the air (as in Forke’s translation of the discussed passage), but qi . Although Forke’s translation is possible, the semantic field of the notion qi was much broader than just “air” (for both similarities and differences between Greek aēr and Chinese qi see Lloyd, Sivin 2002).⁴

Wang Chong criticizes a theory that explains the change of the day and night as well as the seasons by alternating preponderance of the Yin and Yang fluids:

儒者曰：「日朝見，出陰中；暮不見，入陰中。陰氣晦冥，故沒不 見。」 …… 儒者曰：「冬日短，夏日長，亦復以陰陽。夏時，陽氣多，陰 氣少，陽氣光明，與日同耀，故日出輒無鄣蔽。冬，陰氣晦冥，掩日之 光，日雖出，猶隱不見，故冬日日短，陰多陽少，與夏相反。」 (Huang Hui 1990, 11.32/485)

“The Literati say that the sun, when he becomes visible in the morning, comes forth from Yin [darkness], and that, when he disappears in the evening, he re-enters Yin [darkness]. The Yin qi [of darkness] is obscure, [they say], therefore the sun disappears in it, and becomes invisible …

They [again] say that the shortness of the days in winter, and their length in summer are also brought about by the Yin and the Yang. In summer, the Yang qi abounds, and the Yin qi falls short. The Yang fluid shines with the same splendour as the sun. Consequently, when the sun comes forth, there is nothing to obscure him. In winter, the Yin qi is dusky, and overshadows the sun-light. Therefore, although the sun rises, he remains dark and invisible. Thus in winter the days are short. The Yin in paramount, and the Yang is scarce, just the reverse of what takes place in summer” (transl. Forke, 258 f., with minor adjustments).

This doctrine corresponds to Heraclitus’ theory of bright and dark exhalations as one can infer from its exposition by Diogenes Laertius:

“Exhalations arise from earth as well as from sea, some are bright and pure, others dark. Fire is fed by the bright exhalations, the moist element by the others … The bright exhalation, set aflame in the hollow orb of the sun, produces day, the opposite exhalation when it has got the mastery causes night; the increase of warms due to the bright exhalation produces summer, whereas preponderance of moisture due to the dark exhalation brings about winter” (D.L. 9; 11; transl. R. D. Hicks, slightly corrected).

Although Diogenes’ exposition is rather vague, one can nevertheless observe an important point of difference between Heraclitus’ version and that presented by Wang Chong. Reading the latter, we are not in a position to understand how actually the mechanism works, what brings about the cycle of alternating preponderance of the Yang and the Yin. In the case of Heraclitus, we understand at least that the whole process has something to do with the sun, with its action upon either earth or sea.

It is worth further noting that Heraclitus’ version requires two premises. First, to depend on exhalations from earth and sea, the sun must be small relative to the whole body of the Earth. Second, since both kinds of exhalations are caused by the activity of the sun, the regions above which the sun makes its passage during the winter and during the summer must be essentially different, that is, about a half of the surface of the Earth must be continuously (more or less) covered by sea. Both premises agree well with the ideas current in Ionia of Heraclitus’ time. Anaximenes maintained that the sun was much smaller than the earth (Daiber 1980, 399; the testimony not figures in DK and Wöhrle’s Anaximenes). Heraclitus wrote several decades after Scylax of Caryanda had sailed the Indian Ocean (c. 518–515 BC; Schiwek 1962, 16, n. 85; Panchenko 2002, 10 f.; Panchenko 1998). He knew accordingly that there was an immense body of water far in the south and thus had a good reason to think that on a winter day the sun makes its way exclusively or so above the sea, while in the summer it moves mostly above the dry land of India, Arabia, Ethiopia and Libya.5

For China, there is no problem with the first premise. The size of the sun was estimated to be 1000 li (as in the Lunheng ) or 1250 li (as in the Zhou bi ). As to the second premise, there is nothing in the Lunheng to suggest that Wang Chong is aware of the huge expanse of the Indian Ocean (though he addresses geographical matters). Nor is there any clear reason to assume such knowledge in China in earlier times.

To be sure, in China earth and water both belonged to the Yin category, and thus usually were not contrasted; each had its own opposition of Yang nature: heaven for the earth and fire for the water. Moreover, the ultimate source of Yang qi was heaven, and the source of Yin qi, the earth; the water seems to have never been thought of emitting the qi. This may suggest that the similarity between the doctrine discussed by Wang Chong and Heraclitus’ theory is illusive. This also may on the contrary suggest that the doctrine in question comes from a source outside the elaborate Chinese tradition of correlative thinking.

The option that the theory criticized by Wang Chong originated in Ionia finds support in the very kind of criticism he offers:

如實論之，日之長短，不以陰陽。何以驗之？復以北方之星。北方之 陰，〔冬〕日之陰也。北方之陰，不蔽星光，冬日之陰，何故猶(獨) 滅日明？ (Huang Hui 1990, 11.32/485–486).

“However, if we consider the question seriously, we will find that the Yin and the Yang are not responsible for the length or the shortness of the days … This is made evident by the northern stars. The Yin of the north is the Yin of the winter day. The Yin of the north does not overshadow the sparkling of the stars, why then should the Yin in winter obfuscate the brightness of the sun?” (Forke 1962, 259 with minor adjustments).

The refutation seems excellent. But should we assume that the author of the theory was so careless? If the author was Heraclitus, we saw that several aspects of his theory were consistent. What we further hear about his views is enough to argue that he anticipated the objections raised by Wang Chong.

“He does not make clear the nature of the surrounding (περιέχον). He says, however, that there are in it bowls with their concavities turned toward us, in which bright exhalations collect and produce flames. These are stars. The flame of the sun is the brightest and the hottest; the other stars are further from the earth and for that reason give it less light and heat. The moon, which is nearer to the earth, traverses a region which is not pure. The sun, however, moves in a clear and untroubled region, and keeps a proportionate distance to us” (D.L. 9. 9–10; transl. R. D. Hicks slightly corrected).

Greek ἄστρα can designate stars in general or the so-called fixed stars, or the planets; in some contexts related to the views of the Presocratics the word designates just “sun and moon.” The latter is certainly not the case in the given context. Speaking of “other stars” rather than of the stars in general points to the planets. The fixed stars are in all probability placed by Heraclitus on the heavenly vault – the surrounding; Heraclitus’ universe is a closed world: “the whole (τὸ πᾶν) is limited and forms one world” (D.L. 9. 8). The very idea of a closed world seems to imply that the starry heaven is its cover; there was no need, then, to mention in a special way the stars of heaven. Heraclitus’ system also implies the principle according to which the purity of the celestial region increases with its distance from the earth. We conclude that according to Heraclitus the exhalations from both earth and sea do not affect the perception of the fixed stars and even planets: the exhalations do not reach that far and high.

It follows that Heraclitus’ theory, however peculiar, was carefully thought out. Speaking of people criticized by Wang Chong, Cristopher Cullen suggests: perhaps we have here a variant of the gai tian , “created by those who were unable to accept the usual ‘out of range’ theory and felt the need for some actual physical blockage to explain why the sun was not visible at night” (Cullen 1977, 182). For Heraclitus, this is quite a plausible problem situation.

We have to make a choice between two options: either Wang Chong deals with a theory simplified and somewhat distorted in the long course of transmission (ultimately from Ionia) or the literati criticized by Wang Chong did not indeed care of checking the theory they held against the concomitant phenomena, but were satisfied with an explanation constructed in the spirit of the so-called correlative thinking (then one need not to think of any Greek inspiration). In a way, we are in a position to evaluate the latter option through comparing the possibility with two actual texts. This is stated in the Huainanzi (c. 139 BC):

夏日至，則陰乘陽，是以萬物就而死。冬日至，則陽乘陰，是以萬物 仰而生。晝者陽之分，夜者陰之分，是以陽氣勝，則日修而夜短；陰氣 勝，則日短而夜修。 (He Ning 1998, 3/238)

“At the summer solstice, yin (begins to be) ascendant over yang. For this reason, the myriad creatures come to an end and die. At the winter solstice, yang (begins to be) ascendant over yin. For this reason, the myriad creatures lift up their heads and come to life. Daylight is the portion of yang, night is the portion of yin. Thus when the yang qi dominates, days are long and nights are short. When the yin qi dominates, days are short and nights are long” (Major 1993, 105).

Comparing this passage with Wang Chong’s exposition of the similar view of the literati, one may note that Wang Chong includes a physical aspect, however modestly represented: “the sun, when he becomes visible in the morning, comes forth from Yin [darkness], and that, when he disappears in the evening, he re-enters Yin [darkness];” the phenomenon is described in terms of visible things, which is missing in the Huainanz i passage.

Christopher Cullen cites a rather similar passage from Baihutong , “Comprehensive Discussions at the White Tiger Hall” ascribed to Ban Gu (32–92 AD):

所以必有晝夜何？備陰陽也。日照晝，月照夜。日所以有長短何？陰 陽更相用事也，故夏節晝長，冬節夜長。 (Chen Li 1994, 9/426)

“Why is there always day and night? This is the proper ordering of Yin and Yang. The sun illuminates the day and the moon illuminates the night. Why do the days vary in length? The Yin and Yang takes charge of affairs in turn. Therefore in summer the days are long, and in winter the nights are long” (Cullen 1977, 190).

Cullen tentatively proposes that we hear in the cited passage the voice of “the literati” criticized by Wang Chong, which makes him also remark: “Paradoxically, Wang must be said to have expounded his opponents’ theories more clearly than they did” (Cullen 1977, 191). Cullen does not suggest anything impossible, yet he properly speaks of a paradox. Is it not better to think that Wang Chong had access to the exposition of theories that were more physical in character than the cited passages? One should also not to forget that the opposites of hot and cold, bright and dark, dry and wet were omnipresent in the Presocratic thought (Lloyd 1964; Lloyd 1966, 15–85; Panchenko 2002, 250; Panchenko 2016a, 249–253).

One may observe that while Heraclitus’ theory of exhalations accounts for the seasonal change of the length of the day (and night) it does not explain the seasonal change of the visible altitude of the sun above the earth. It is likely, however, that Heraclitus followed Anaximenes’ theory: “The heavenly bodies turn back in their courses owing to the resistance of compressed air” (13 A 15 DK). Of all celestial bodies that can be meant in the passage, the sun with its movement from solstice to solstice is clearly of predominant interest. How should one imagine the working of the mechanism? The sun (as also the moon and the planets) moves between a solid cover of heaven and a solid bottom of the earth. (In cosmology of Anaximenes, the heavenly bodies move only above the earth; Heraclitus probably followed him.) The sun not only describes daily an orbit above the earth, but also goes half a year down and a half a year up, from solstice to solstice. Although the sun is much smaller than the earth it is still large enough to push a significant amount of air to either solid bottom or solid cover. At some moment, the air either above or below the sun becomes condensed enough to start pushing the sun in the opposite direction.

It seems likely that Wang Chong again had a vague knowledge of this or similar Ionian theory without realizing one important detail. He says:

或曰：「夏時陽氣盛，陽氣在南方，故天舉而高；冬時陽氣衰，天抑 而下。高則日道多，故日長；下則日道少，故日短也。」 (Huang Hui 1990, 11.32/487)

“Some people hold that in summer, when the Yang qi abounds, it is in the south, and that in consequence heaven rises and becomes high. In winter the Yang qi decays, and heaven sinks down, and becomes depressed. When heaven is high, the course of the sun increases in length, and the days are lengthened; when heaven is low, the solar curve decreases, and the days are short” (Forke 1962, 259, with minor adjustments).

The association between the Yin and winter, on the one hand, and the Yang and summer, on the other hand, was of course very strong. The doctrine cited by Wang Chong includes, however, a particular idea criticized by him, and his objection is again powerful. He points to the fact that the supposed alternating shift of heaven up and down does not correspond with the visible positions of the moon in the sky. However, as presented by Wang Chong, “this theory of the pneumatic rise and fall of heaven relies implicitly on the sun being attached to heaven and rising and falling with it” (Cullen 1977, 185). That the sun is somehow attached to heaven seems a strong belief by Wang Chong himself. Although (as mentioned in our section 1) one can find the same belief in reports on the teaching of such a Presocratic thinker as Archelaus (60 A 4 DK), the theory proposed by Anaximenes does not mean it at all and is therefore immune in respect to the objection raised by Wang Chong.

As Cullen 1977, 283 properly notes “there is the further objection, common to all theories involving a relative translation of heaven and earth: why are not less stars visible in winter than in summer?” Anaximenes with his sun and not heaven going alternatively up and down is again immune in respect to the objection. On the other hand, taking such an objection into consideration does not require either intellectual sophistication or careful study of celestial phenomena. On the assumption of an independent Chinese construction of the idea, its author should have been remarkably uncritical – as also those people who made it a part of the intellectual tradition that reached Wang Chong. One cannot cite in this case even the propensity to the correlative thinking. It seems therefore legitimate to consider the possibility that we are here dealing with an echo and distortion of the doctrine once received from an authoritative, ultimately Greek source.

It is appropriate to mention that Wang Chong holds the same basic cosmographic views as Anaximenes. The fact is that the cosmography Anaximenes and the gai tian (‘celestial cover’) are so similar and so specific that one may treat them as one and the same system. According to this system, the sun and the other celestial bodies rotate only above the earth; their setting and rising is nothing but optical illusion caused by the distance (as we all know, the objects appear nearer to the horizon as they recede). The solar illumination extends only to a certain distance; when the sun is farther than that it is no longer visible. The appearance of the starry sky as a dome touching the earth on the horizon is deceptive; in reality it lies in a plane parallel to the surface of the earth (or the surfaces of heaven and earth are symmetrically curved). The celestial pole is the centre of heaven, and the heavenly bodies, including the sun describe their orbits round it. The daily path of the sun can be explained as a circle centred on the celestial pole. It expands during one half of the year, reaching its maximum on the day of the winter solstice, and then contracts during the other half, reaching its minimum on the day of the summer solstice. In this system, the centre of the surface of the earth does not coincide with any privileged land, city or temple; it is strictly beneath the celestial pole.

It should be specified that what is presented above as the Anaximenian type of cosmography is based on the interpretation proposed by one of the present authors (Panchenko 2015; Panchenko 2016a; now supported and developed by Kočandrle 2019). Two main ancient expositions of the gai tian , one found in the Lunheng and another in the Zhou bi suan jing display some differences. The Zhou bi is essentially connected with the gnomon shadow measurements. One rule is here the basis of all calculations: for every 1000 li the shadow of an eight- chi gnomon diminishes or increases by one cun . Thus, if the length of the shadow at the summer solstice noon is 16 cun , this means that we are distant by 16 000 li from the point directly below the sun – the northern tropic. The Milesian origin of this shadow rule was repeatedly argued and may be claimed to be proven.⁶ Wang Chong, however, shows no awareness of the shadow rule (Cullen 1977, 167; 174). Strictly speaking, then, the demonstration of Greek origin is valid only for the type of measurements presented in the Zhou bi , while it is still possible, in principle, to defend the independent origin of the main ideas of the gai tian . This is the way that Dirk Couprie choses (with an important qualification: Couprie 2018, 326).

Yet one has to bear in mind that Anaximenes had both the gnomon measurements of the specified type and the ideas common with the gai tian . If the books representing two branches of the gai tian , the Zhou bi and the Lunheng by Wang Chong display various and sometimes different signs of the dependence on Anaximenes, and if in the case of the Zhou bi the dependence can be taken as proven, then it is reasonable to take seriously the possibility that the branch represented by Wang Chong is also of Greek origin.

While the ant simile proves the reality of a link between Wang Chong and early Greek thought, another case seems to prove a link between Wang Chong and mature Greek science. While defending the system of the celestial cover with its emphasis on the phenomena of optical illusion, Wang Chong maintains: “To men heaven and earth seem to unite at a distance of no more than ten li . That is the effect of the distance, for they do not come together in fact” (Forke 1962, 261). Dirk Couprie makes a very important observation: “Curiously, what Wang Chong calls the apparent distance of the horizon, ten li , is just about the real distance (i.e. on a spherical earth) of the horizon (4.66 km) for a person of an eye height of 1.7 m” (Couprie 2018, 275 f., with n. 28 and Fig. 13. 8 providing both mathematical explanation and illustration; see also Couprie 2011, 182 f.). Let us consider the implications of such a striking fact.

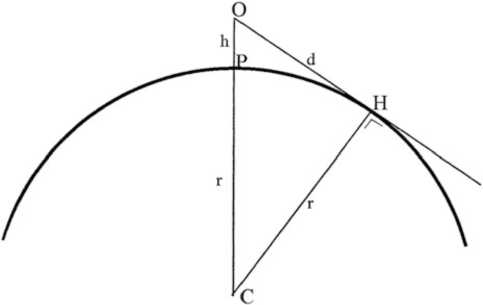
Fig. 1. Calculation of the real distance of the horizon (after Coupri 2018, 276, Fig 13. 8)

Despite qualification “no more than” Wang Chong’s statement claims to be precise; it does not invite taking ten as just a round or for example number. Wang Chong does not claim, however, that his confident declaration is based on his own inquiry. Nor is it likely that in fact it is. Since it is common experience that one sees further from an elevated place Wang Chong’s statement makes sense only on the assumption that any elevation is consciously disregarded, but he does not specify that. Moreover, is there any empirical way to determine the distance of the horizon? In principle, one may note some markers that look located very near the place where heaven and earth (or watery surface) seem to unite. To be sure, such markers are difficult to imagine since it is problematic that houses or trees will be seen clearly enough from a distance of 4.66 km. But suppose such a difficulty is overcome. Nevertheless, as one starts to measure the distance in question one soon sees the horizon clearly behind the selected markers, which undermines one’s confidence that the markers initially were indeed very close to the place where heaven and earth seemed to unite. Suppose the measurements were repeated and even in various locations, suppose the opinions of a several persons concerning the proximity of the markers to the apparent horizon were taken into account, suppose such repeated efforts brought about the conviction that the distance of the horizon is about 9 li, perhaps a bit less or more, but certainly no more than 10 li – all that is not something to be ruled out as impossible. But all that is certainly most unlikely. For it is very difficult to see what could be the problem and goal of the person who committed or initiated such a laborious and insecure enterprise. Wang Chong cites 10 li in order to point out that heaven and earth “do not come together in fact”. This is appropriate rhetorically, but irrelevant logically, for everybody knows that the line along which heaven and earth seem to unite will ever recede as one advances; the specified distance of ten li adds nothing to the argument. Finally, the idea of empirically found distance of the horizon is unlikely for the reason that a person deliberating such an enterprise could hardly hope to convince other people of the validity of the result to be achieved in the described way.

We may conclude that finding the distance of the horizon was not an achievement of Wang Chong himself and that he followed an authoritative source. We may also conclude that in all probability the achievement in question was made not in an empirical way. But then it was made in a theoretical, scientific way; indeed, the very confidence of Wang Chong’s statement suggests that it goes back to a scientific result. In that case the authoritative source of his statement must be ultimately Greek! As Couprie’s Fig. 13. 8 (our Fig. 1) makes it clear, in order to determine the distance of the horizon one has to know the radius of a spherical earth. The sphericity of the earth was a specifically Greek teaching. Measuring the circumference of the earth, and thus knowing its radius, was a specifically Greek achievement. On the contrary, the idea of a spherical earth, even if vaguely heard of, did not constitute a part of Chinese cosmological tradition (Cullen 1977, 386– 390). When Wang Chong offers once an estimate of the size of the earth (Forke 1962, 256), the numbers he cites find a remarkable correspondence with early Greek efforts to measure the earth on the basis of the cosmography of Anaxime-nian type (Panchenko 2024), while it is clear that he does not have in mind a spherical earth.

The very idea of measuring the distance to the horizon could be inspired by diagrammatic representation of the most famous Greek method of measuring the circumstance of the earth, the method of Eratosthenes (c. 276–195 BC), according to which the shadow casting gnomon is considered as an extension of the earth’ diameter (Fig. 2), in an analogous way to a person looking at the horizon in Fig. 1.

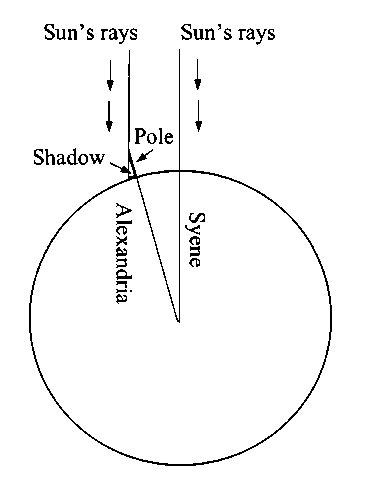
Fig. 2. An illustration to Eratosthenes’ method of measuring the earth.

Moreover, the problem itself was almost certainly solved before Eratosthenes. It is stated in a Greek popular introduction to astronomy written by Geminus (probably first century BC): “There are two horizons—one perceptible [to our sight] and the other perceivable by reason. The perceptible horizon is the one described by our vision in accordance with the limitations of sight, and it has a diameter no larger than 2,000 stadia” (V, 55 – 56; Evans, Berggren 2006, 158, slightly modified). We shall shortly see that 3 stadia corresponds to 1 li. This means that Geminus’ figure requires an explanation. A basically correct one was proposed in recent translations of Geminus. Evans and Berggren note: “If the perceptible horizon has a maximum diameter of 2,000 stadia, then we can see for 1,000 stadia … A simple geometrical calculation shows that the rim of the horizon is 1,000 stadia away for an observer standing on a mountain 12.5 stadia high. (We assume Eratosthenes’ figure of 252,000 stadia for the circumference of the Earth given by Geminos at xvi 6.) Since Geminos puts the heights of some remarkable mountains at 10 to 15 stadia (xvii 5), these geometrical considerations probably motivated his choice of 1,000 stadia for the maximum possible distance of the perceptible horizon” (Evans, Berggren 2006, 158, n. 30). Andrei Shchetnikov, the translator of Geminus into Russian, gives 12 stadia (instead of 12.5) and briefly remarks: “Perhaps this result was calculated by Dicaearchus” (Shchetnikov 2011, 195, n. 39). He apparently means that Di-caearchus had the reputation of a measurer of the mountains. Although the reference by Evans and Berggren to the mountains of 15 stadia high contradicts their own calculations, and although all the cited commentators do not specify what value of π they take, the most accurate or rounded to 3 (as is often the case even with competent ancient authors), and although their mathematical results are devoid of truly appealing elegance (with 42 000 stadia for the radius of the earth, the distance to the horizon is 1025 and 1004 stadia respectively; with 40 127.4 stadia for the radius of the earth, it is 1002 and 981 stadia respectively) their main ideas hit the mark.

It is clear that Geminus means not a distance to the horizon seen in an open space from a level ground, but he speaks of the extreme visual range, which opens from the highest available mountain. Now, Dicaearchus, a disciple of Aristotle (384–322), reputed among other things for measuring the mountains estimated that highest mountains (measured by him) reached 10 stadia. This follows from the words of Pliny the Elder of Dicaearchus, “a man of great learning, who measured the mountains with great care, of which Pelion was the highest, measuring 1250 paces” ( HN 2. 162; fr. 105 Wehrli; fr. 118 Fortenbaugh). The most common equation of the Roman mile was to 8 stadia , and hence 125 (double) paces = 1 stadion , 1250 paces = 10 stadia .

We further hear from Archimedes that an authoritative estimate of the circumference of the earth (preceding, as clear from the context, the famous measurement by Eratosthenes) was 300 000 stadia ( Aren . 1. 8), and Dicaearchus is the only candidate known by name to introduce this figure. It is hardly in doubt that the number as round as 300 000 implies π = 3, with the corresponding radius of the earth = 50 00 stadia . One can see that (50 000 + 10)² – (50 000)² = 1 000 100; and √1 000 100 = 1000,05. Thus the value given by Geminus (2000 stadia for the double distance to the horizon) fits perfectly well with the circumference of the earth equal to 300 000 stadia . We need not decide whether Dicaearchus introduced (as was repeatedly suggested) or just accepted this value for the circumference of the earth. We may, however, safely deduce that another value, 1000 stadia for the maximum range of human sight, was established on his data – most likely by Dicaear-chus himself.

It is beyond a reasonable doubt that one able to measure the maximum range of human sight is also able – and will do – to measure a usual range of human sight, unassisted by elevation. In other words, the problem of the distance to the horizon was recognized and solved by Greek science c. 300 BC at the latest.

Now, an original Greek formula of the distance to the horizon was of course formulated in Greek measures, stadia. Although one can find plausible examples of Greek stadia substituted for Chinese li, this is not the case we are dealing with: although the length of a stadion varied, even 10 largest stadia would make less than a half of the cited above 4.66 km. We should consider then a likely procedure of converting stadia into li.

Greek stadion is a complicated matter to be addressed here briefly and with a particular purpose in mind. A classic passage on Greek linear measures in Herodotus (2. 149) implies a stadion of 600 feet. Translating Roman mile (which is 1000 double paces) in terms of stadia , ancient authors give varying equations: most frequently 8, but also 7, 7.5, 8 1/3, and 10 stadia per mile. The pace as a unit is ignored in Herodotus’ passage. There is no doubt, however, that distances along the roads were measured by counting paces and not feet. We hear of special bēmatistai (“those who measure by paces”) in service to Alexander the Great and know that Eratosthenes used their accounts in his geographical work that essentially influenced the subsequent Greek geographical tradition. Varying equations of the mile (of a length around 1480 m) to stadia indicate that the latter did not always measure the same distance. It may seem most surprising that main Greek authors on geographical matters nevertheless use the term stadion as we do the terms kilometer or mile, that is, they show no awareness that different stadia were of somewhat different length. This puzzle may be resolved on the assumption that ancient authors took it as a matter of course that all measured roads were measured by counting paces (typically double paces) and that accordingly all distances expressed in terms of stadia implied a stadion of hundred paces. That the length of a pace and accordingly of a stadion can in fact vary was too obvious to them to specify it.

Further, it was systematically argued that though directly attested in the Zhou bi the shadow rule was in fact established in the sixth century Miletus; that this original shadow rule stated the change of the shadow length cast by a gnomon by one eightieth of its height for every 1000 stadia = 78.75 km since one stadion was defined as 100 single paces equal to 3 feet by 26.25 cm; that the relics of the early Ionian stadion defined as 100 single paces are repeatedly found in Greek and Latin geographical texts; that the only way to determine the basic distance used by Eratosthenes to calculate the circumference of the earth, which was the length of the arc between the latitude of Alexandria and the latitude of Syene, was to resort to the shadow rule; and that the stadion built in Eratosthenes’ measurement of the earth meant 100 paces – however, double as it became common in Greek world since the fifth century, that is, 78.75 x 2 = 157.5 m (Panchenko 2016 a, 91–147).

The stadia cited by Dicaearchus probably derived from the same old Ionian tradition. Scholars commonly blame Dicaearchus for the inaccuracy of his measurements (Wehrli 1967, 75; Keiser 2017, 356 – 361) precisely because they underestimate the fact that a stadion was a matter of change. Relying on most common equation 1 Roman mile = 8 stadia (which naturally secured prominent place in various encyclopedias), they take without any further justification Dicaearchus’ stadion to mean 185

m. This would be reasonable for the times of the firmly established Roman rule (Shcheglov 2015, 65), but not for the late fourth century BC; a contemporary of Roman conquest of Greece, most competent Polybius considered Roman mile to be equal to 8 1/3 stadia (Strab. 7. 7. 4). Meanwhile it is possible (on a couple of most plausible assumptions) to calculate the length of Dicaearchus’ stadion with a significant precision.

In another passage, Geminus argues that clouds are so to speak a terrestrial and not celestial phenomenon. He asserts that clouds “do not reach even up to 10 stadia in height”, for which he gives a proof as follows: “Those who climb Kyllene, the highest mountain in the Peloponnesos, and sacrifice to Hermes, to whom offerings are made on the summit of the mountain, find, when they climb again and perform sacrifices a year later, that the thigh bones and the ashes from the fire remain in the same condition in which they had left them, and that they have not been changed by winds or by rainstorms, because all the clouds and the formation of the winds occur below the summit of the mountain” (XVII. 2 – 3; Evans, Berggren 2006, 217). If one asks now the question of what height of Kyllene implies the story, the only natural answer will be no more than 10 stadia , which will not of course admit the possibility of the height being 9 or 8, etc. stadia , but will signify just slightly less than 10 stadia . Geminus says so and refers to Dicaearchus; the manuscript reading gives, however, “less than 15” instead of expected 10 stadia . This makes the whole rather meaningless, while in accordance with the logic of the passage the above cited testimony of Pliny implies that Dicaearchus never measured a mountain higher than 10 stadia . The manuscript version, 15 stadia , seems to reflect a later measurement mentioned by Strabo (8. 8. 1). A Greek author, be that Geminus, his source or his editor, combined and confused the name of a famous measurer and the advanced result. We conclude that the figure given by Dicaearchus was in fact 10 stadia (in all probability he measured this inland mountain as it rises above the plain of Stymfalia, while a later geographer measured Kyllene as it rises above the sea level, which is 2376 m and yields 158.4 m per stadion ).

Now Apollodorus of Athens, a learned historian and grammarian of the second century BC is cited for the assertion, made in his work On the Gods, that Kyllene is “9 Olympic stadia, without 80 feet high” (FGrHist 244 F 130). One should not think of a measure related to the length of the stadium in Olympia; Olympic stadion was a term meaning the stadion of 600 feet (Cens. DN 13). Apollodorus did not measure the mountain himself. He just converted the received value that went back to Di-caearchus into the terms demonstrating his learning (for he claimed to be precise giving 5400 – 80 = 5320 feet for the mountain height) and comprehensible to his readers. The best attested Attic foot = 29.6 cm (Dekoulakou-Sideris 1990). Converting Attic feet into our measures we receive 1574.72 m for the height of Kyllene. On the justified assumption that Dicaearchus gave 10 stadia (and neglecting his “slightly less”, as Apollodorus clearly did) we receive 157.47 m for his stadion.7 This is in perfect agreement with the Eratosthenean stadion of 157.5 m inferred both many years ago (Hultsch 1882, 61) and recently, by one of the present authors, in a very different way.8

To sum up, although this is not directly stated in the sources, Greek stadion actually meant 100 (double) paces rather than 600 feet, and there was an influential tradition that lasted for centuries of reckoning with stadia of 157.5 m. One may now easily understand how a Greek formula was translated into Chinese. It turns out that Greek stadion and Chinese li are essentially similar measures, both based on counting paces. One li is defined as 300 bu , that is, paces, perhaps single originally, but double in the Eastern Han. Hence one li is about the same as 3 stadi a, and there will be 30 stadia behind the 10 li cited by Wang Chong.

To be sure, 4.66 km calculated by Couprie for a person of an eye height of 1.7 m corresponds to modern measurements of the earth, and the results obtained on the basis of the ancient measurements were certainly somewhat different. Assuming a stadion of 157.5 m, one may calculate that for the radius of 50 000 stadia and an eye height of 157.5 cm the distance to the horizon will be 31.6 stadia and for an eye height of 173.25 cm will be 33.2 stadia ; for the radius of 42 000 stadia and an eye height of 157.5 cm he distance to the horizon will be 29 stadia and for an eye height of 173.25 cm will be 30.4 stadia . Eratosthenian version fits better with Wang Chong’s 10 li , yet the difference with the earlier measurement is not essential.⁹

On the Chinese side, the length of one li in Wang Chong’s time, c. 415 m may seem to present a problem. Since 30 stadia by 157.5 m are equal to 4725 m the Chinese equivalent would be 11 rather than 10 li . However, the ancients were not in a position to relate their respective national measures to an international system. They would have counted paces without converting them in meters and 30 stadia would have been identified as 10 li anyway. Still it is worth noting that such a short li of c. 415 m is a peculiar feature of the Eastern Han. One li of the (late) Zhou epoch is estimated to have been 477.84 m and that of Qin, possibly inherited by the Western Han, 497.7 m (Kroll, Romanovsky 1982; their data is based on the studies by Chinese and Japanese scholars). The knowledge of the distance to the horizon could easily reach China earlier than the Eastern Han. Whatever the date, the conclusion seems inevitable that the person who converted 30 stadia to 10 li understood both Greek and Chinese systems of linear measures. Whatever was Wang Chong’s source, the link in the discussed case between Greek and Chinese worlds of thought is hardly disputable.

Let us sum up. We have ants crawling on a rolling mill-stone, in both Greece and China. This is an indisputable, we assume, case of transmission.

We have air and qi (barely distinguishable from air in the context) that knows everything everywhere. The repeated independent construction of such an idea is possible, but not very likely.

We have apparently identical and most peculiar theories explaining the change of seasons, in both Greece and China. The Chinese version looks like a reduced and simplified Greek original, but this would be an exaggeration to say that such a conclusion is unavoidable.

We have the extravagant Chinese theory that involves seasonal rise and fall of the sun attached to heaven. However, if the sun is not attached to heaven the corresponding theory turns reasonable and ingenious. Precisely such a version of the theory is attested for Anaximenes whose views display many links with the views that circulated in China. Moreover, Wang Chong holds the same basic cosmo-graphic views as Anaximenes.

Wang Chong has a correct idea of the distance between the observer and the horizon, but this normally requires knowledge of the radius of the spherical earth, which suggests the Greek origin of the numerical data available to Wang Chong.

165 cm (Schwartz 2013, 167). The average distance from the eyes to the vertex is about 10 to 13 cm.

It seems to follow that there was something to connect Wang Chong with both the early and mature Greek cosmology. There is no reason to assume that Wang Chong had direct access to Greek sources. He possibly dealt with echoes of Ionian ideas long ago embedded in China, on the one hand, and with some more recent ideas that came from the Hellenistic world, on the other hand. Somewhat different scenario is also imaginable. Beginning with the fourth century BC, professional astronomy became increasingly difficult to comprehend by laymen, and there appeared and gained the popularity in the Hellenistic world various dilettante teachings that combined in a bizarre way elements of both early and advanced science. Such teachings could travel very far.

Wang Chong’s views display, however, no familiarity with the contemporary Hellenistic science of astronomy. If the correct estimate he gives of the distance to the horizon is not a mere coincidence with reality, but an echo of Greek science, he shows the knowledge only of the formula and not of astronomical and geometrical principles behind it. His familiarity with astronomy in general seems very limited. To be sure he says once: “On an average, the eclipse of the sun occurs every 41 or 42 months, and an eclipse of the moon, every 180 days” (Forke 1962, 271; cf. Huang Hui 1990, 11.32/506). Yet confidence in his statement hardly matches the views of contemporary astronomers. It is true, lunar eclipses occur typically twice a year. There is indeed a solar eclipse cycle equal to 41 synodic months, but there are better cycles and a cycle of 42 months is idiosyncratic. Wang Chong seems not aware of either the shadow rule or of the book, the Zhou bi suan jing , in which it plays a central part. Not an even implicit reference to the hun tian school appears in his discussions.

As a key element in the story of transmission of Ionian ideas, one of the present authors suggested the emigration of the Branchidae, a community governing the important temple of Apollo near Miletus, to Sogdiana in 479 BC (Panchenko 2002). Early contacts between China and the region to which the city of the Branchidae belonged are documented in the so-called Sogdian letters. Though written in the early fourth century AD, they still refer to China as Qin and the Chinese capital as Xianyang, thus reflecting the situation earlier than 200 BC (Henning 1948, 608). No objection has been raised against this suggestion, so it remains valid. The penetration of Greek ideas into China after Zhang Qian opened the way to more or less regular contacts between the Han Empire and Hellenized Central Asia requires no special explanation.