Типизация территории методами геостатистического анализа по физико-географическим факторам

Пермский край занимает первое место на Урале по обеспеченности водными ресурсами. Основная часть рек относится к бассейну Камы, который характеризуется сложностью, обусловленной разнообразием форм рельефа. Реки края имеют преимущественно снеговой тип питания с четко выраженным весенним половодьем. В период половодья в зону затопления могут попадать жилые дома, земли сельскохозяйственного назначения, объекты социальной сферы и экономики, в том числе потенциально опасные объекты. Повышение эффективности мероприятий по защите от наводнений может быть достигнуто при системном учете всех факторов, влияю-

• ^*Работа выполнена при финансовой поддержке гранта РФФИ №11-05-96026-р_урал_а.

щих на формирование половодья. Одной из основных задач прогнозирования уровня воды в реках и предотвращения негативных последствий затопления территории в весенний период является исследование процессов снеготаяния [1].

Цель данной работы – типизация территории водосборов методами геостатистиче-ского анализа по физико-географическим факторам для моделирования пространственного распределения интенсивности снеготаяния.

Для исследования был выбран бассейн реки Язьвы. Авторы располагают, во-первых, электронным слоем границы этого бассейна, а также цифровой моделью его рельефа, представленной в виде растра с пространственным разрешением 1000 м, каждый пиксель которого содержит высоту над уровнем моря соответствующего участка местности.

Известно, что на интенсивность снеготаяния влияют, в том числе, и такие физикогеографические характеристики местности, как высота исследуемого участка над уровнем моря, величина его уклона, а также экспозиция склона. Поскольку территория, на которой тестируется модель, велика, то целесообразно поделить ее на участки, однородные в смысле упомянутых выше характеристик. Подходящий для этого инструмент - кластерный анализ.

Для проведения кластерного анализа из цифровой модели рельефа бассейна реки Язь-вы был получен точечный слой пространственных объектов. Каждый объект характеризуется набором признаков: высотой соответствующего участка местности над уровнем моря, экспозицией склона, на котором находится этот участок, а также его уклоном. Высота над уровнем моря измерена в метрах, экспозиция - в градусах от направления на север, а уклон - в градусах от горизонтали. Высота над уровнем моря взята непосредственно из цифровой модели рельефа (ЦМР), а экспозиция и уклон - результаты ее обработки посредством инструментальной геоинфор-мационной системы ArcGIS.

Анализируемый класс пространственных объектов представлен на рис. 1. Интенсивность цвета соответствует высоте объектов над уровнем моря.

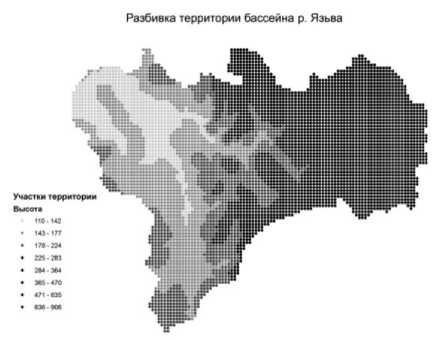
Рис. 1. Анализируемые территории

• 1.    Описание алгоритма выделения однородных групп пространственных объектов

  Обозначим через

  
  

  S = { X i , i = 1, N }

  
  

совокупность анализируемых пространственных объектов. Каждый объект представляет собой трехмерный вектор. Задача состоит в том, чтобы разбить совокупность на однородные группы (кластеры), учитывая только ре- зультаты измерений характеризующих объекты признаков.

Для этой цели используется одна из наиболее известных процедур кластерного анализа - метод k -средних. Данный метод принадлежит к группе итерационных методов эталонного типа. Ее смысл состоит в последовательном уточнении на каждой итерации эталонных точек (средних арифметических многомерных наблюдений, попавших в образовавшиеся кластеры) [2]. Таким образом, в геометрическом пространстве векторов-признаков определяются довольно плотные структуры.

Доказано, что в результате применения метода k-средних всегда находится решение (последовательность итераций сходится), однако конечный результат сильно чувствителен к выбору начального разбиения. В связи с этим предлагается в качестве начального разбиения использовать результат кластеризации объектов иерархическим методом полных связей [4]. Центры тяжести образовавшихся кластеров в дальнейшем могут рассматриваться как эталонные точки начального разбиения в процедуре метода k -средних.

Еще одной особенностью метода k- средних является то, что исследователь должен располагать информацией о количестве однородных групп в структуре анализируемого множества объектов еще до проведения кластеризации. Однако такая априорная информация не всегда доступна. Поэтому возникает необходимость обосновывать полученный результат разбиения. Для этого в данной работе используется функционал качества разбиения вида

m

^ = ZZ d ² ( X. ,X i ) .

l = 1 X i е S_l

Здесь m — количество кластеров в разбиении, X = ( x ⁽¹⁾, x ⁽²⁾, x ⁽³⁾) - центр тяжести кластера с номером l , d ( X i , X_l ) - евклидово расстояние между объектом X , принадлежащим кластеру с номером l и центром тяжести этого кластера.

Функционал (1) характеризует разброс объектов внутри кластера (плотность кластера). Наилучшим считается разбиение, при котором достигается минимальное значение этого функционала [3]. Таким образом, последовательно применяя метод k -средних для k =1,2… и вычисляя значение функционала (1)

для каждого полученного разбиения, можно определить наиболее оптимальную типизацию объектов.

Перед применением вышеописанной процедуры кластерного анализа целесообразно применить нормировку исходных стати- стических данных с использованием следующих формул:

x

*( q ) ₌

ν =

x ( ^q ) - x⁽ q ) a qq

nn

x(q) = 1∑xν(q); σ(q) =   1∑(xν(q)-x(q))2, n ν=1                  n ν=1

где q = 1,2,3 – размерность вектора характеристик пространственных объектов, ν = 1, 2, ... n – количество анализируемых объектов. Такое преобразование необходимо, так как первая характеристика объектов измерена в метрах, а другие – в градусах. В результате получаем безразмерные координаты для каждой многомерной точки наблюдения.

Авторами работы разработано приложение для выполнения описанной выше процедуры [5]. Входные данные – исходная совокупность объектов, сохраненная в базе данных MS Access. Выходные данные – текстовый файл, содержащий сведения о принадлежности объектов к кластерам в различных разбиениях, а также значения функционала (1) для этих разбиений.

2.    Результаты

Кластерный анализ проводился для выборки, состоящей из 5 886 объектов. Каждому из них были назначены следующие атрибуты:

• •    высота над уровнем моря;

• •    экспозиция склона;

• •    уклон склона.

Кроме того, для каждого объекта известна точка его местонахождения на электронной карте.

Выборка разбивалась на 2, 3, 4,… 10

кластеров. Для каждого разбиения вычислялось значение функционала (1). Результаты расчетов представлены в табл. 1 и на рис. 2.

Таблица 1. Значения функционала (1) для различных разбиений

Количество кластеров	Значение функционала
2	15 517,70
3	9 400,61
4	17 253,49
5	16 110,43
6	19 640,10
7	16 790,57
8	5 152,36
9	7 688,13
10	11 250,81

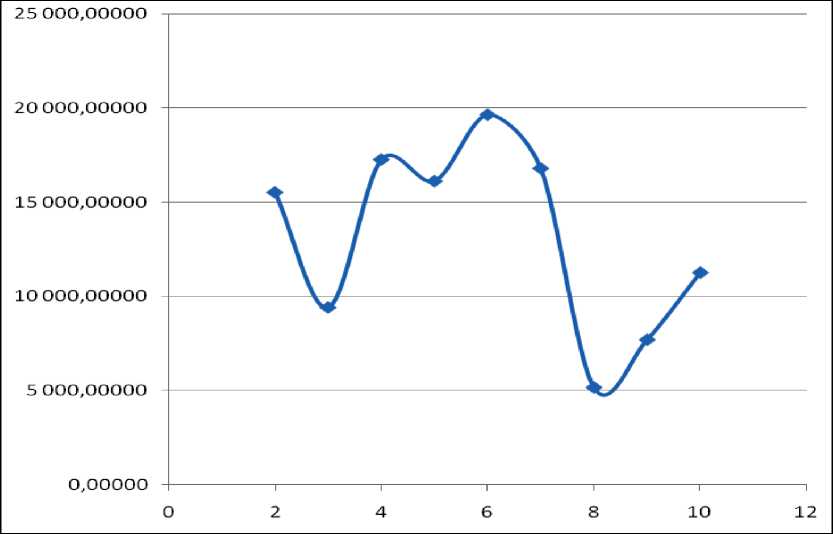
Рис. 2. График значений функционала (1) для различных разбиений

На рис. 2 по оси Ox отложено значение числа кластеров в разбиении, по Oy – значение функционала (1). Легко видеть, что локальные минимумы функционала достигаются при разбиениях, состоящих из трех, пяти и восьми кластеров, причем "наилучший" минимум получается для восьми кластеров. Изображение слоя электронной карты, где каждая точка-объект раскрашена в зависимости от номера кластера (для случая 8 кластеров), к которому она принадлежит, представлено на рис. 3.

Разбивка территории бассейна р. Язьва

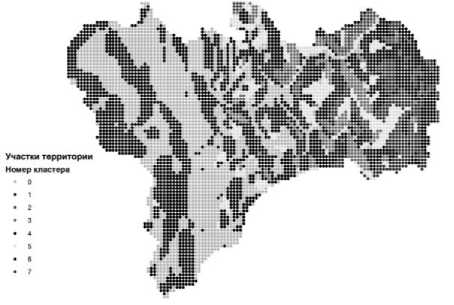
Рис. 3. Разбиение территории на 8 кластеров

Из рисунка видно, что, несмотря на то что при анализе не брались во внимание географические координаты объектов, нам удалось получить разбиение на компактные группы, отражающие характерные формы рельефа изучаемой местности. Статистика по каждому кластеру представлена в табл. 2.

Если учитывать средние значения физико-географических характеристик и сред-невкадратичные отклонения по ним, то из таблицы видно, что кластеры хорошо разделены по совокупности характеристик. Например, первый и второй кластеры пересекаются по высоте, но разделены по экспозиции.

Заключение

Таким образом, полученные результаты могут быть использованы в дальнейшем для построения наиболее качественной математико-картографической модели расчета процесса снеготаяния.

В дальнейшем планируется включить в анализ данные о растительном покрове местности.

Таблица 2. Статистика по кластерам

№	§ м й S о а 5 н ® h F   У S ^ g Ч “ 2 О Ч у п д	3 и и	й u S ^ о К й «кой «не® о g 2 о & & Н д и °	со	и и g s й о к к и о    К й д М н w ж о О « g М И и Й О о и & 2	ж а >ч и	Ml М 5 2 и § ч й о ” ° и 5 й Г о sr и U н
1	1926	180,80	45,52	272,82	47,28	0,40	0,31
2	1531	171,28	39,51	73,81	47,33	0,45	0,32
3	128	421,78	91,29	186,37	53,56	3,76	0,66
4	331	338,44	84,80	77,12	55,81	2,06	0,53
5	810	354,16	80,27	280,42	40,63	1,71	0,51
6	476	345,84	99,03	159,49	59,82	0,73	0,37
7	287	684,58	101,40	251,30	54,53	2,91	0,62
8	397	554,18	90,67	258,46	55,15	1,10	0,51