Transversal domination in double graphs

Lot G be a graph. A subset S of vertices is called a dominating set of G if every vertex not in S is adjacent to at least one vertex in S. The minimum cardinality of a dominating set is called the domination number, denoted by y (G) F°^r an у graph G, there may be many dominating sets of different cardinalities between y ( G ) ^and the order of G. The concept of transversal domination in graphs is defined and studied in [1]. A dominating set is called the transversal dominating set if it intersects every minimum dominating set in G. The minimum cardinality of a transversal dominating set is called the transversal domination number, denoted by Ytd(G). In [1], authors have obtained fundamental results related to transversal domination parameter including exact values for standard graphs and bounds in terms of order and domination number.

Let G and H be any two graphs. The direct product of G and H is a graph denoted by G x H with the vertex set V(G) x V (H ) such that two vertices (v1,w1) and (v₂,w₂) are adjacent in G x H if and only if v1 aiid v₂ are adj;icent in G and w1 aiid w₂ are adjacent in H. The total graph Tn of оrder n is the graph associated to the total relation (where every vertex is adjacent to each vertex). In fact, Tn can be obtained from the complete graph K_n by adding a loop to every vertex. Given a simple graph G, the double of G is a simple graph

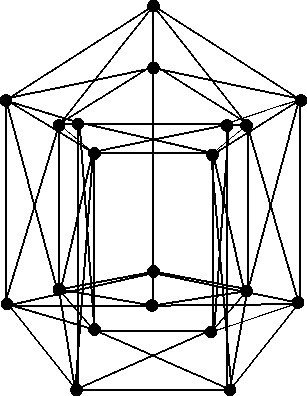
From the definition of a double graph [2], it follows that if G is a graph of order n and size m then D(G) is a graph of order 2n and size 4m. In particular, the degree of a vertex (v,k) will be 2degG v. The pentagonal prism with modified lateral edges and its double graph are as shown in Figure 1. The double graph D(G) always decomposes into two subgraphs Go and G1 such that Go П G1 = 0 aiid Go U G1 is a spanning subgraph of D(G). T1 юн {Go,G1} is called the decomposition of D(G). The double graph operation is defined for any graph G, throughout this paper, by a graph G, we mean a graph without loops and multiple edges. The multi-star graph K_m(ai, a₂,..., am) is a graph of order ai + a₂ + • • • + am + m formed by joining a1,a₂,...,a_m eiid-eiIges to m vertices of Km. For ex ample. K₂(a1,a2) is a double star.

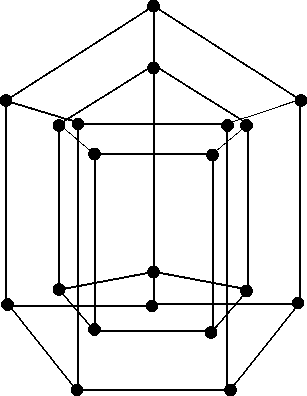
Fig. 1. Double graph of a Pentagonal prism.

Lemma 1.1. Let G be a path of order n. Then

Y (D(G)) =

{2L n J,

12L 3 J +1,

if n = 0 or 1 (mod 3);

if n = 2 (mod 3).

Theorem 1.1. Let G be a path of order n ^ 3. Then Ytd(D(G)) = y (D(G)) + 1.

• <    Let G be a path of order n. Since the Y-set of D(G) is obtained by choosing vertices from the Y-set of copies of G, it will be clear that there are atmost two possibilities to select vertices from a Y-sct of copies of G. Thus, for any vertex u of Y-set of G which is riot in Y-set

S оf D(G), the set S U {u} will be a dominating set intersecting the minimum dominating sets in D(G). Minimality" of the set S1 = S U {u} since for tmy vertex v of S1. there always exists a Y-set of D(G) riot intorseeting S1. Ho neo. Y.d(D(G)) = y ( D ( G )) + 1 »

Lemma 1.2. Let G be a complete graph. Then y ( D ( G )) = 2.

Theorem 1.2. Let G be a complete graph of order n. Then Y.d(D(G)) = 2n — 1.

• < 1 Lel G be a complete graph of order n. Tlюн D(G) will be a regular graph order (2n — 2). Since every pair of vertices, taken from each copies of G, is a dominating set it follows that Ytd(D(G))=2n — 1. ▻

Theorem 1.3. Let G be a cycle of order n > 4. Then

(5,

Y (D(G)) = 3,

if n = 4;

if n = 5;

^2[ П3 J, otherwise.

• <    Lcl,. G be a cycle of order n ^ 3. Tlion D(G) is a 4-rcgular graph of order 2n. If n = 4. then clearly y ( D ( G )) = 5. Assume n = 5. Then, any minimum dominating set of a copy of G. in which a vertex u of S replaced by the corresponding vertex u¹. will be a minimum, dominating set and so y (D(G)) = 3.

7.d(D(^G)) = ^ф_     n_{n s 2(m-Kj3}).

Now. suppose n ^ 6. We may consider three possible cases here. First, suppose n = 3k. As the graph D(G) consists of two copies of C_n. choose a minimum dominating set S ‘ of one copy, which dominates D(G) except the vertices corresponding to the vertices of S'. So that, the set S obtained by taking the vertices not dominated by S’ togetlier with S ‘. will be a dominating set of D(G). Further, for any vertex v of S, the set S — {v} will not be a dominating set in G and so in D(G). Thorefore. y ( D ( G )) = 2|S‘| = 2^П3J.

Next, suppose n = 3k + 1. As in the previous case, clioose a minimum dominating set S’ of a, copy G arid then select the correspoiigiiig vertices from another copy of G. Tins will be a dominating set but not minimal as the vertices v1 and v^ have two neighbors in the set. Hence, S ‘ — {v1, v^} will be a minimum, dominating set in G. Therefore. y ( D ( G )) = |S‘ — {v1, v^}| = 2LП3J. FinaUy. if n = 3k + 2. similar to the above case, for any set S ‘ consists of vertices from y- set of G arid the corresponding vertices in other copy of G. the set S = (S’ — {v1, v_n-1})U{v^} will be a minimum dominating set of cardinality 2|П3J. >

Theorem 1.4. Let G be a cycle of order n > 3. Then f 2L nJ +3, ifn = 0or1(mod3);

• <    Lel.. G be a cycle of order n ^ 3 arid let V(D(G)) = {vi,vj : 1 C i, j C n}. First we note that any minimum dominating set in D(G) contains a vertex from V‘ = {vi,v₂,v2 , v_n,v_n, }• Lei, H be a spanning sub-graph of G having the vertex set V — V‘. Tl1011 Y.d(D(G)) = Y(H) + |V‘|- Further, it car1 be rioted that H will be isomorphic to a double graph D(P_n-3)-Therefore. Y.d(D(G)) = y (D(P_n-3)) +5. establisliiigg the result. >

Theorem 1.5. Let G = K_m(ai, a₂,..., am) be a multi-star. Then Y.d(D(G)) = m + 1.

• <    Let G = K_m(ai, a₂,..., am) be a multi-star of order a1 +a₂ + • • ^+a_m. Ciearly y (G) = m. Consider the double graph of G and the minimum dominating set S. As every vertex in S covers the leaves adjacent to it and the vertices adjacent to the corresponding vertices in another copy, it follows that S itself a minimum dominating set in D(G). Therefore, y (D(G)) = |S| = m. Finally. since D(G) contains exactly two r-erte.c disjoint dominating sets. Y.d(D(G)) = m + 1. >

Definition 1.1. For m >  2, Jahangir graph Jn,_m is a graph of order nm + 1, consisting of a cycle of order nm with one vertex adjacent to exactly m vertices of C_nm at a di stance n to each other. Jahangir graph J₂,₁6 is shown in figure 1.

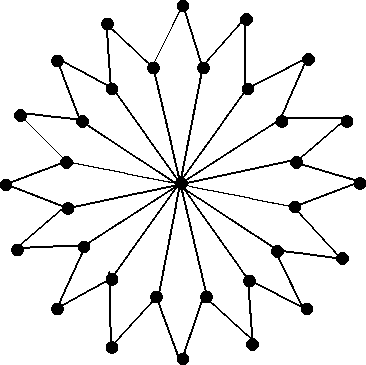
Fig. 2. J2,16.

Proposition 1.1 [3]. Let G = J₂,m be a Jahangir graph with m >  3. Then

Y (G) = |

2,

Г mm 1 +1,

if m = 3; otherwise .

Theorem 1.6. Let G = J_n,_m be a Jahangir graph with m,n >  3. Then

Y (G) = |

mn-¹) + 1, nn = 1(mod3);

Гmn 1, nn = 0 or 2(mod 3).

• < 1 Let G = J_n,_m be a Jahangir graph with m, n > 3 and let V(G) = {v₁,v₂,... ,v_nm,v_nm+₁}. wliere vnm+1 is the vertex at the ceriter. adjacent to vertices of C_nm. First assume n = 1(rnod 3). i. e.. n = 3k + 1. for some positive integer k. From the definition, the vertex v_nm+₁ is adjacent to m vertices of C_nm at a distaiice 3k + 1. Removing the vertex v_nm+₁ fr* mi G. the graph induced by V (G) — {v_nm+₁} splits into m comp orients each component isomorphic to Рзк. Therefore, the minimum dominating set of G is obtained by taking dominating set from each component together with v_nm+1. That is, if S = U^Si, where Si denotes Y-set of i^th component, then SU{v_nm+1} will be a minimum dominating set of G. Since any vertex not in S U{v_nm+1} will be adjacent to exactly one vertex in S U{v_nm+1}. no proper subset will be dominating set in G. Thus, y(G) = mn s ¹ + 1-

• Next, suppose n = 2(mod 3). Here, we may consider three possible cases. First, assume m = 0(inod 3). T1 urn {vm,v2m, V3m,..., vnm} will be a, doriihiathig set of cardinality nm. Ou the other hand, let D be a, dominating set in G and assume vnm+1 G D. As the vertex vnm+1 dominates m vertices, to cover the remaining vertices, at least mГ31 vertices are necessary. Thus, we must have, |D| ^ mrn 1 + 1, which is not possible. Hence, vnm+1 / D. This shows that the domination number of G co-incides with that of a cycle. Therefore, y(G) = Гnm 1-Next, suppose m = 1(mod 3). In this case {v1, V3, V6,..., vnm-1} will be a dominating set of size nm^^, i, e., Гn3m 1- On the other hand, as in the above case, it is easy to observe that vnm+1 / D f°i‘ siiy domhiating set D of G. Therefore, y(G) = Гnm 1-
• Finally, assume n = Q(mod 3). For am' integer m ^ 3. ele;rrly nm will Ire a iMultiple of 3. Further, no dominating set D contains the center vertex vnm+1. He nee, y (G) = Y(Cnm), i- e-> Y(G) = nm. ▻

Proposition 1.2. Suppose m > 3 and n = 1(mod 3), then ytd (Jn,m) =

mn^-1) + 2, mm = 3;

^{m ( n} 3^{- 1)} + 1,    otherwise.

• < 1 Let J_n,_m be a Jahangir graph with m ^ 3 and n = 1(mod 3). If m = 3, then J_n,3 contains three minimum dominating sets among which two of them having a common vertex. Thus, Ytd(Jn,m) = m ⁽n3 1) + 2- Next, Assume m ^ 4. Then, J_n,_m contains three minimum dominating sets. The dominating set {3, 7,11,... , v_nm-1, vnm+1} intersects other two sets and hence itself become a transversal dominating set. Therefore, Ytd(J_n,_m) = m ^(?3 1) + 1- ▻

Theorem 1.7. Suppose m ^ 3 an d n = 1(mod 3), then 7 (D(J_n,_m )) = 2y (J_n, , m )•

• <    Let J_n,_m be a Jahangir graph with m >  3 and n = 1(mod 3). Let S be any minimum dominating set of J_n,_m. Then, S dominate the double graph D(J_n,_m) except the corresponding vertices of S in the other copy of J_n,_m. Since none of the vertices in S have common neighbor in itself, the minimum dominating set of D(J_n,_m) is obtained by adding the corresponding vertices of S. Therefore, Y(D(Jn,m)) = 2 y ( J _n, , _m )• ▻

Proposition 1.3. Suppose m ^ 3 an d n = 1(mod 3). Then Ytd(D(Jn,_m )) = y (D( J n, , m))-

• <    Let J_n,_m be a Jahangir graph with m ^ 3 and n = 1(mod 3). We observe that J_n,_m contains a unique dominating set, the double graph D(J_n,_m) also contains only one dominating set and hence. Ytd(D(Jn,m)) = Y(D(Jn,m))- ▻

Theorem 1.8. Let G = J_n,_m be a Jahangir graph with n = 2(mod 3). Then

⌈m3n⌉

+ 2,

Ytd(G) = < Гm 1 +1,

j mn 1,

if m = Q (mod 3);

if m = 1 (mod 3);

if m = 2 (mod 3).

• <    Let G = J_n,_m,m >  3 be a Jahangir graph such that n = 2(mod 3). First, we note that dominating set in J_n,_m arises from dominting set of the cycle C_nm and hence any transversal dominating set in J_n,_m contains at least one vertex from the set D = {v1,v₂,v3}. There are three possible cases here, suppose m = Q(mod 3), th en nm = Q(mod 3). Th us, J_n,_m contains exactly three vertex disjoint dominating sets each of cardinality nm. Therefore Ytd(G) ^ nm + 2. Ou the other 1 land, since any 7-set contains vertex from D. it follows that Ytd(G) = 3+ y ( H )-where H is the graph induced by V(J_n,_m) — D. Clearly, H = P_mn-5 and hence, Ytd(Jn,m) = Г nm 1 +2. Sup pose m = 1(mod 3), th en J_n,_m contains two vertex disjoint dominating sets. Hence, Ytd-set °f Jn,m is obtained by adding one vertex to the Y"^set °f Jn,_m- Therefore, Гmn 1 + 1. Finally, suppose m = 2(mod 3). As the graph J_n,_m contains only one dominating set {v1, v₄, V7,..., v_mn-4, v_mn-1} and hence itself a transversal dominating set. Therefore, Ytd(Jn,m)= Y(Jn,m)= Гmn 1- ▻

Theorem 1.9. Let G = J_n,_m be a Jahangir graph with n = 2(mod 3). Then Ytd(D(G)) = 2Г nm 1 — _L m-L j + 1 _Furlhcn Ytd(D(G)) = Y(D(G)).

• <    Let G = J_n,_m be a Jahangir graph with n = 2(mod 3). Let S be a minimum dominating set in G. Then, S dominates the double graph D(G) except the vertices in the second copy of G corresponding to that of S. Also, the vertex v'n_m+1 at the center will be adjacent to

exactly L m- ¹J vertices of S. Hence, the minimum dominating set will be obtained by choosing |S| - L m^-1 J vertices from the second copy of G. Therefore. Yt_d(D(G)) = 2^nm1 — Lm-^-1 J +1. Next, since any dominating set in D(G) contains the center vertex vnm+1, it follows that any Y-set itself a transvers al dominating set in D(G). He nee. ym( D ( G )) = Y (D(G))- ▻

Proposition 1.4. Let G = J_n,_m be a Jahangir graph with n = 0(mod 3) an d m >  3. Then Ytd(G)= Y (G)-

• < 1 Let G = Jnm be a Jahangir graph with n = 0(mod 3) and m > 3. For any value of m, we have nm = 0(mod 3) am 1 so G contains unique dominating set {v1, v₄, V7,...■ v_nm 5, v_{nm 2}}-Therefore. Ytd(G) = Y(G) = Г ... 1 - ▻

Theorem 1.10. Let G = J_n,_m be a Jahangir graph with m >  3. If n = 0(mod 3), then y ( D ( G )) = nm + 1. ’

• <    Let G = J_n,_m be a Jahangir graph with m > 3 and n = 0(mod 3). Si nee G contains a unique dominating set D = {v1, v₄, V7,..., v_nm 5, v_{nm 2}} and the set fails to dominates the corresponding vertices in the second copy of G. Therefore, y (G) ^ nm + 1- On other hand, since the center vertex vnm+1 is adjacent to every vertex in D, the set D U {vnm+1} will be a dominating set and hence, y ( D ( G )) = nm + 1- ▻

Theorem 1.11. Let G = J_n,_m be a Jahangir graph with m >  3. If n = 0(mod 3), then Ytd(D(G)) = nm + 2. ’

• <    Let G = J_n,_m be a Jahangir graph with m ^ 3 and n = 0(mod 3). From the above theorem, it follows that G conatins exactly two dominating sets having no vertex in common. Thus adding one vertex from a dominating set to other set, the transversal dominating set will be obtained, therefore, Ytd(D(G)) = nm + 2. ▻

• 2. Bounds for Ytd( D (G))

Theorem 2.1. Let G be any connected graph of order n. Then 1 C y (G) C y (D(G)) C Ytd(D(G)) C 2n. Further, y (D(G)) = Ytd(D(G)) holds if a.nd only GG contains a unique dominating set of size 1.

• <    Let G be any connected graph of order n. Since any dominating set of double graph of G dominates G also, it follows that y (G) C Y (D(G))- Ass time y (D(G)) = Ytd(D(G)). On contrary, suppose y ( G ) ^ 2 and let S be a Y-set. Then S dominates the double graph D(G) except the corresj"wilding vertices of S in other copy of G. Therefore. S cannot Ite a transversal dominating set in D(G), showing that y (D(G)) = Ytd(D(G)). Conversly, if G contains a unique dominating set of cardinality one, then D(G) contains unique dominating set and so y ( D ( G )) = Ytd(D(G)). ▻

Corollary 2.1. Let G be any graph. Then 2 C y ( D ( G )) C Y td( D ( G )). Further, Ytd(D(G)) = 2 if and only GG is a star.

• <    Let G be any graph. First, assume Ytd(D(G)) = 2. From the above theorem it follows that y (D(G)) = Ytd(D(G)) am 1 so G must contain exactly one vertex of degree n — 1. proving that G is a star. Com"erse is obvious. ▻

  There is no exact relation between Ytd(G) and y (D(G)). For example, if G is a star, then y ( D ( G )) = Ytd(D(G)). Let G be a complete graph of order n ^ 4. theii Ytd(G) = n — 1 > 2 = y ( D ( G )). Finally. lol, G be a path of Рб- T11011 Ytd(G) = 5 bi it y (D(G)) = 6.

Proposition 2.1. Let G be a connected graph of order n ^ 2. Then Ytd( D (G)) C y ( D ( G ))+ d( D (G)).

• < 1 Lel G be a connected graph of order n ^ 2. Tlten. 6(G) ^ 1 and lei, v Ire a vertex of degree 6(G). Clearly, any demiinating set in D(G) must, contalii either v or a vertex from N ( v). Thus. Ytd(D(G)) <  Y(D(G)) + | N ( v )l- Tins pr<>ves that. Ytd(D(G)) ^ y ( D ( G )) + 6 (D( G )). ▻

Theorem 2.2. Let G be any graph. Then Ytd(D(G)) = 2n — 1 if and only if G is a complete graph.

• <    Lel, G be a connected graph of order n. Assume that Ytd(D(G)) = 2n — 1. Them any subset S' of vertices of order almost 2n — 2 is not a transversa 1 dominating set in D(G). From the minimality of Ytd(D(G))- T follotvs that. V — S ' = { u, v } is a domimtting set in D(G). Furl,her. V — S ' must contains at least one vertex from each copy of G. Thus, y ( G ) = 1- As the vertices u. v are chosen arbitrarily. each vertex in G must have degree n — 1. proving that G is a complete graph. Converse is obvious. ▻