TVD-модификация метода Годунова 3-го порядка

DOI:

В последние два десятилетия прошлого века широкое распространение получили нелинейные разностные методы 2-го порядка аппроксимации по пространству и времени, обладающие повышенной устойчивостью на разрывных решениях. С начала века активно развиваются нелинейные методы более высокого порядка аппроксимации по пространству и времени. В своем большинстве такие методы являются полудискретны-ми [6; 8; 11; 12], реализующими два этапа аппроксимации дифференциальных уравнений в частных производных. На первом этапе с помощью кусочно-полиномиальной реконструкции строится дискретный разностный оператор для производных по пространству, в результате чего получается система обыкновенных дифференциальных по времени уравнений размером по количеству ячеек сетки. На втором этапе к этой системе применяются методы Рунге — Кутта 3-го или 4-го порядка по времени.

Отдельная дискретизация по пространству и времени упрощает построение метода, однако она существенно расширяет шаблон разностной схемы и требует дополнительных мер для обеспечения TVD-свойства, что приводит к увеличению количества стадий в методе Рунге — Кутта и порождает заметную диссипацию численного решения [6; 12]. Использование метода Рунге — Кутта для аппроксимации по времени впервые предложено в [14]. Позже эти же авторы в [15] пришли к выводу, что совместная аппроксимация является более эффективной.

В работе [4] предложен полностью дискретный метод 3-го порядка, использующий совместную дискретизацию уравнений по пространству и времени без использования стадий Рунге — Кутта. Этот метод является расширением метода Годунова 2-го порядка [1] за счет подключения двух отдельных блоков коррекции потоков. Первый блок повышает аппроксимацию для линейных систем уравнений, а второй устраняет погрешность, возникающую из-за нелинейности уравнений.

В первом разделе представлено компактное описание метода [4] без подробных обоснований. Во втором разделе сформулирована и доказана теорема о монотонности разностной схемы метода применительно к модельному уравнению переноса при использовании адаптивного TVD-лимитера центральных разностей [9]. В заключение раздела приведен способ построения новых модифицированных лимитеров, удовлетворяющих условию теоремы о монотонности.

На тестовых примерах показано, что новые лимитеры улучшают точность решения как в окрестности сильных и слабых разрывов, так и в окрестности локальных экстремумов решения.

В третьем разделе приведены описание метода для системы уравнений газовой динамики и результаты расчетов стандартного теста [16] с применением новых лимитеров.

1.    Общий вид модификации схемы Годунова 3-го порядка

Изложение схемы проведем на примере однородной гиперболической системы уравнений законов сохранения du   д f (и)

dt Эх

Пусть сетка является равномерной с шагом h, причем направление роста номеров ячеек (г) совпадает с направлением оси координат х. Разностная схема Годунова с шагом т по времени для г-й ячейки будет иметь вид иг+1 -«Г   /(и+1)— /(и- 1)   п v                v |                 2                       2   0J

т              h где и" ~ u(xi,tn) — приближенное решение в центре г-й ячейки. Величины с полу-целыми индексами ui+1 представляют собой значения параметров на границе между ячейкам, на которых вычисляются потоки. В методе Годунова 1-го порядка эти величины являются результатом решения задачи Римана с аргументами из смежных ячеек.

В методе 2-го порядка [1] в задаче Римана используются аргументы с поправками U i + ди и Н г₊₁ + du _{i +1} , где поправки аппроксимируют выражение (^hu _— + - и)/2. По сути применяется линейная реконструкция по координатам ж, t на границы ячеек и на половинный шаг по времени. Для вычисления поправок производные по времени следует выразить через пространственные производные, используя свойство решения дифференциального уравнения

U t _ —J (u)u - ,

где J(и) _     .

ди

В методе 3-го порядка [4] выполняется квадратичная реконструкция, которая реализуется в виде двух этапов линейной реконструкции по схеме Горнера.

Для нелинейной / (и) квадратичная реконструкция потоков отличается от квадратичной реконструкции параметров и на величину 2-го порядка малости, которая в [4] учитывается введением дополнительных потоков N на последнем этапе коррекции

N _ ^(т ² J t U t — h^J - u - Y

Устойчивость разностной схемы, аналогично схеме Годунова, обеспечивается использованием процедуры ^ точного решения задачи Римана с параметрами и ± на границах между ячейками.

С учетом сказанного один шаг по схеме 3-го порядка состоит из следующих четырех этапов.

• 1)    Первый уровень левых и правых поправок во всех ячейках (индексы опущены)

  и

  
  
  
  

  _ и —

  
  

  ^и - — 3J (и)и -

  
  

  U⁺ _ и |— и_х —

  6 ^х

  
  

  τ

  3J (u)U - .

  
  
  
  

• 2)    Второй уровень левых и правых поправок во всех ячейках

  и _ U — ^U - — ^J (и )й ^- ,

  
  

  и ⁺ _ и + -и_х — - J(и ⁺ )и + . —                —

  
  
  
  

Вычисление производных и _х на этих этапах осуществляется по трем точкам с использованием гладких TVD-ограничителей [2; 10].

• 3)    Предиктор, дающий решение и 2-го порядка

  и — и"   / (ui+1) — / (ui- 1)

  - +     2        2

  т

  
  

  где ^и + 2 ^_ ^(и+^+у) .

  
  
  
  

• 4)    Корректор с нелинейными потоками, дающий решение и "⁺¹ 3-го порядка

и "^¹ - U i + ^N 1 - N ¹ т            h

= 0 ,

где нелинейные потоки (4), например, по формулам

„   _ ( J (и , ) - J (и " ))(п - и " )    ( J (п +1 ) - J (u ? ))(u ?_h -и " )

N i — ------------------- — ---------------------- i+2                24                               24

Нелинейные потоки (4) можно вычислять с 1-ым порядком точности.

Формулы (5)–(9) описывают этапы одного шага для схемы Годунова 3-го порядка: предварительный шаг (7) с поправками первого (5) и второго уровня (6) плюс шаг коррекции (8) с нелинейными поправками третьего уровня (9).

2.    TVD-свойство схемы 3-го порядка

В этом разделе проведем обоснование монотонности вышеописанной схемы 3-го порядка применительно к модельному уравнению переноса, свойства решений которого хорошо известны

Зи    Зи.

— + о— — 0 , о — const > 0.(10)

atox

Обозначим через u _i и U _i приближенные значения и(х) в ячейке г в моменты t и t + т соответственно. В этих обозначениях схема Годунова 1-го порядка для (10) запишется в виде двухточечной схемы

U i — U i - v(Ui - U i- 1 ) ,

где v — о^Т , h

которая устойчива и монотонна при выполнении условий

0 6 v 6 1.                                     (12)

Для вычисления производных в поправках первого и второго уровня схемы 3-го порядка будем использовать лимитер центральных разностей

£(^a,b) ^— |

sign(a) min(2 0 |a|, s(|a|, |b|), 2 0 1&|), if

0 ,

if

^ab> ⁰                a + b

, где s(a,b) — ab 6 0                   2

с адаптивным ограничивающим коэффициентом θ ,

зависящим от ν

_      1

max( v , 1 - v )

1 6 0 6 2.

Заметим, что при 0 — 1 адаптивный лимитер (13) совпадает с обычным лимитером центральных разностей [9]. Функция £(a, b) удовлетворяет очевидным свойствам, которые будут использованы далее

|£(a,b)| 6 min(2 0 |a|, 2 0 |b|);      ^(a, b) — £(b, a);

С(а + |е|,Ь) > £(а, b);     С(ка,кЬ) = к £(а, b).(16)

Для каждой ячейки г введем обозначение Au _i разностей против потока

Aui = Ui -Ui-1.(17)

Для модельного уравнения переноса (10) отсутствуют нелинейные потоки (8) и решение задачи Римана Р(и+ ,u-+1) = и+. В результате схема (5)-(7) будет состоять из трех этапов1

• 1)    Ui = Ui + т(1 - 2v)C(Aui, Aui+i),(18)

о

• 2)  Ui  =  Ui + ^(1 - v)£(Aui, Aui+i),(19)

• 3)  Ui  =  ui — vAui.(20)

Теорема 1. Разностная схема (18)–(20) с функцией-ограничителем (13)–(14) и с числом Куранта (12) является TVD-схемой.

Доказательство. Из (15) следует, что разность функций ℒ с общим аргументом можно записать в виде равенства с некоторым коэффициентом ц , зависящим от а, b, с:

£(а, b) — С(с, а) = 2ц0а,      где |ц| 6 1.(21)

При объединении (18)–(20) в одну формулу применим это равенство два раза

^(Aui, Aui+i) — ^(Aui-i, Aui) = 2n0Aui,(22)

P(A-Ui, AUi+1) — £(AUi-i, AUi) = 2ц0AUi.(23)

Получим одно соотношение для схемы с двумя коэффициентами | ц | 6 1 и | п | 6 1

Ui = Ui — v(1 + (1 — v)ц0(1 + 3(1 — 2v)n0)^ Aui.(24)

Таким образом схема (18)–(20) формально приведена к двухточечной схеме (11), но с переменным коэффициентом v _i , зависящим от решения

Vi = v(1 + (1 — v)^0(1 + 3(1 — 2v)n0)),     |ц| 6 1, |n| 6 1.(25)

Двухточечная схема с переменным коэффициентом v _i будет TVD-схемой, если выполнены условия v _i >  0 и 1 — v _i >  0 [7]. С учетом (12) проверка этих условий сводится к проверке неравенств для двух функций

Р(v, ц,п) = 1 + Ц0(1 — v)(1 + 3П0(1 — 2v)) > 0 ,(26)

Q(v, ц,п) = 1 — ^0v(1 + зn0(1 — 2v)) > 0 .

Прежде чем проверять выполнимость этих условий, установим связь между коэффициентами ц и п . Введем параметр р, для которого с учетом (12) выполнено

|1 — 2v| р =    '    , ' ,   ^   0 6 р 6 1.(28)

max( v , 1 — v)

Далее оценим величины с крышкой в (23).

1I

Au = Aut + -(1 - 2v)2n0Au^ = (1 + k^Aut,    где Щ 6 -.(29)

Обозначим для краткости А = £(Au _t , Au _t+i ), А = £(A4, Au _{t +i} ). Пусть Au _t >  0, тогда из условий (16)

А = Г((1 + k^Au, (1 + k_H i )Au_H i ) 6 Г((1 + k _A )Au t , (1 + k _A )Au t +i ) = (1 + k A ) А,

А = £((1 + kt)Aut, (1 + kt+i)Aut+i) > Г((1 - kA)Aut, (1 - kA)Aut+i) = (1 - k^, где kA = max(|kt|, |kt+i|) 6 |/3. Эти два неравенства объединим в одно |А - А| 6 kA|А|. Случай Aut < 0 приводит к точно такой же оценке. Аналогичные оценки выполенны и для величин В = £(Aut-i, Aut) и В = £(Aut-i, Aut). В результате с учетом первого свойства функции-ограничителя (15) будем иметь

• |А -А| 6 I|А| 6 ^|Au t |,     |В -В| 6 ||В| 6 2| 0 |Au t |.         (30)

В обозначениях А и В система (22)-(23) приводится к виду

А -В = 2 n6 Au _t , А -В = 2 ц0 (1 + k _t )Au _t .               (31)

Вычитаем в (31) первое уравнение из второго, переходим к модулям и учитываем ранее выведенные оценки (29) и (30). Получим

• 2| ц - n | 0 |Au _t | = |А -А -В + В - 2 ^0 k _t Au _t | 6

• 6 |А - А| + |В -В | + 2| ц0 k _i Au _i | 6 2| 0 |Au t |, откуда непосредственно следует связь между коэффициентами µ и η :

| ц - п | 6 |.                                       (32)

Таким образом, обоснование TVD-свойства схемы сводится к необходимости доказать, что неравенства (26) и (27) для функций В ( v , ц , п ) и Q( v , ц , п ) выполнены в диапазоне аргументов 0 6 v 6 1, | ц | 6 1, | п | 6 1, | ц - п | 6 |.

Для фиксированного ν диапазон представляет собой шестиугольник в плоскости ( ц , п ), изображенный на рисунке 1.

Заметим, что функции Р и Q связаны центральной симметрией

Q(1 - v, -ц, -п) = Р(v, ц,п),     Р(1 - v, -ц, -п) = Q(v, ц,п), поэтому доказательство достаточно провести для 0 6 v 6 2.

По аргументам ( ц , п ) функции Р и Q являются гармоническими, то есть Р _цц +Р _пп = = 0 и Q _цц + Q _пп = 0, следовательно, их максимум в шестиугольнике достигается на границе шестиугольника. Задача сводится к проверке экстремумов функций одного переменного на шести сторонах шестиугольника. На сторонах АВ, АР , CD и DE (рис. 1) функции линейны, на сторонах ВС и FE функции квадратичны с точкой экстремума за пределами диапазона. То есть на всех сторонах шестиугольника функции либо монотонно возрастают либо монотонно убывают. В этом случае для проверки неравенств (26) и (27) достаточно вычислить и проверить значения функций в вершинах шестиугольника

^А( ц = ^{- 1,} п = ^{- 1)},    ^В( ц = ^{- 1,} п = ^{- 1+}1),    ^{С (} ц =1 ^- I, п = 1),

D( ц = 1, п = 1),         E ( ц = 1, п = 1 -1),       F ( ц = -1+ 1, п = 1).

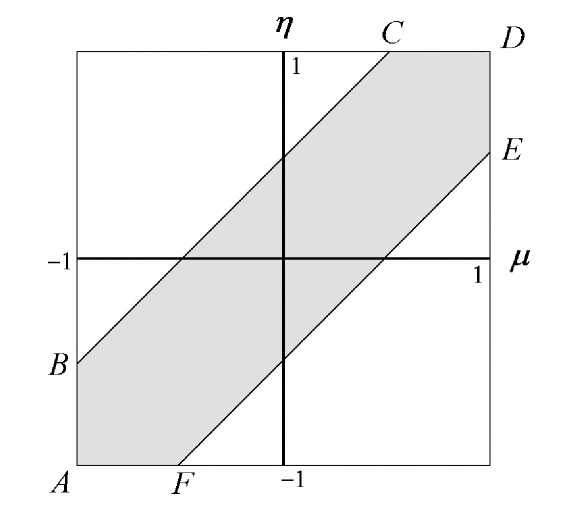
Рис. 1. Область возможного изменения параметров µ и η функции устойчивости в (25)

Опуская несложные выкладки, выпишем значения функций Р и Q в вершинах, используя для краткости обозначение q = p/3:

Р (Л) = q,

^{Р ( в} ) = ^{(1 -} p)q,

Р(С ) = 1 + (1 - p)(1 + q),

Р (D) = 2 + q,

Р(Е ) = 2 + (1 - p)q,

^{Р ( F} ) = ⁽⁴ - p)q,

Q(Л) = 1 + (1 - p)(1 - q), ^{Q ( B} ) = ¹ +^{(1 -} p ^{)(1 -} q^{(1 -} p))

^{Q ( c} ) = ⁽5 ^- р ^- p ^{2 )}q,

Q(D) = (2+ p)q,

^{Q ( E} ) = ^{(2 + 2}p ^- p ^{2 )}q,

Q(F ) = 1 + (1 - p) ² (1 - q).

С учетом диапазона изменения 0 6 p 6 1 видим, что значения функций во всех вершинах неотрицательны. Следовательно, схема (18)–(20) при условиях (12)–(14) обладает TVD-свойством. Теорема доказана.

Заметим, что в вышеприведенном доказательстве непосредственные свойства функции среднего арифметического s(a,b) в формуле (13) не использовались. Вместо нее в лимитере (13) может быть и любая другая функция s(a,b), обладающая следующими свойствами при положительных аргументах:

s(a, b) = s(b, a),

ds n

> о, da

s(ka, kb) = ks(a, b),

s(a, a) = a,

ds

da

a = b

.

Здесь последнее свойство требуется для обеспечения 3-го порядка аппроксимации разностной схемы. Такими свойствами обладает известная функция среднего гармонического и ряд других функций [2; 5]. Для построения новых аналогичных лимитеров можно использовать следующее утверждение: если s(a, b) при положительных аргументах удовлетворяет условиям (33), то этим же условиям удовлетворяет и функция

• s(a,b) = s(a,b)(1 + r(1 — d)²d), где d = — ,    ,  0 6 r 6 3V3.     (34)

max(a, b)

Добавка в (34) приближает лимитер к известному лимитеру “superbee” [13], сохраняя гладкость и положительность в указанном диапазоне коэффициента г.

Далее в тестовых расчетах использовались лимитеры /(a,b), C(a,b), M(a,b), которые при аргументах одного знака (ab >  0) имеют вид

/(a, b) = sign(a) min(2|a|, s(|a|, |b|), 2|b|),(35)

C(a, b) = sign(a) min(20|a|, s(|a|, |b|), 20|b|),(36)

M(a, b) = sign(a) min(20|a|, s(|a|, |b|), 201b|),(37)

где s(a,b) и 0 из формул (13)-(14), а s(a, b) из формулы (34) с коэффициентом r = 3V3.

Известным недостатком TVD-схем является эффект срезания локальных экстремумов численного решения. На рисунке 2 представлены тестовые расчеты влияния вышеприведенных лимитеров на численное решение модельного уравнения переноса (10) с ст = 1 с треугольным профилем точного решения после длительного перемещения.

Начальный треугольный профиль состоит из левого линейного участка шириной на 0,2 и высотой 5 и правого разрыва. Расчеты проводились на отрезке [0,1] с периодическими граничными условиями на сетке со 160-ю ячейками и числом Куранта CFL= 0, 6. Результаты расчетов для трех лимитеров изображены на момент времени t = 5, то есть на момент, когда начальный профиль проехал расстояние 5 длин расчетной области.

По рисункам видно, что адаптивный лимитер С чуть меньше срезает экстремум, а в остальном его действие мало отличается от лимитера С. Модифицированный адаптивный лимитер М помимо существенно меньшего срезания экстремума значительно лучше выдерживает как фронт переднего разрыва, так и подножие сопряжения линейного участка с константой.

Заметим, что повышение качества решения не требут значительных затрат, так как лимитер М получается из лимитера С простыми арифметическими операциями.

3. Реализация схемы 3-го порядка для уравнений газовой динамики

Система дифференциальных уравнений, описывающая законы сохранения массы, импульса и энергии для нестационарного течения идеального совершенного газа в трубе постоянного сечения в одномерном приближении имеет следующий вид:

д w    d f

dt дх где

	ρ		p v
w =	p v	, f =	p v 2 + р
	е		(е + p)v _

Здесь р (х, t), р(х, t), v(x, t) — плотность, давление и скорость газа зависят от координаты х вдоль трубы и времени t. Полная энергия единицы объема газа е = p(y — 1) ^{- 1} + + p v²/2 (для воздуха у = 1,4). Вектор массовых переменных w (плотность, импульс, энергия) используется для записи законов сохранения. Вектор традиционных переменных u = ( р , р, v) обычно используется для ввода/вывода и анализа результатов.

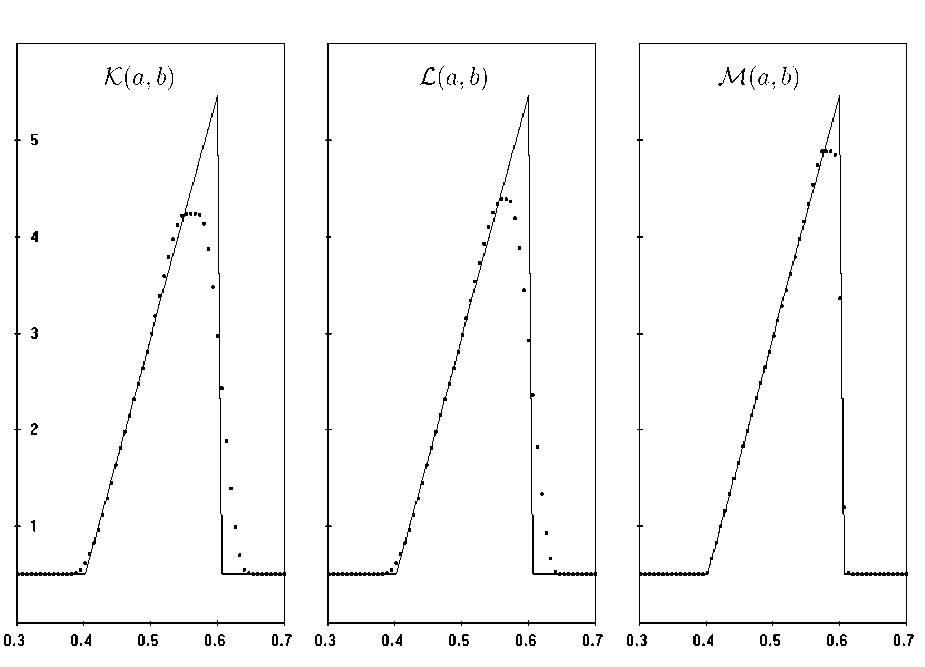
Рис. 2. Сравнение численных решений с разными лимитерами (35)–(37) для модельного уравнения переноса (10) с с = 1 на решении с треугольным профилем. Сетка из 160 ячеек на отрезке [0,1] с периодическими граничными условиями, CFL = 0, 6.

Результаты показаны на момент времен t = 5

Систему уравнений (38)–(39) можно записать с производными по времени от u du    . дu

= 0,

+ АТТ dt дх где

ρ		V	0	ρ
р	, А =	0	V	Y P
V		0	р - 1	V

Пусть выбрана равномерная по х сетка c шагом h, причем направление роста номеров ячеек г совпадает с направлением координаты х. Схема Годунова для системы (38) записывается в следующем виде:

wp - w P    ^{f ( u} i+ 1 ) ^{- f ( u} i - 1 )   _n

+2—2— = 0 т              h где w)+1 — вектор параметров в ячейке г в момент tP + т. Величины с полуцелыми индексами представляют собой параметры на границах между ячейками. Они находятся из решения задачи Римана с условиями из прилегающих ячеек. В линейном приближении для системы (40) это решение имеет вид:

u” + u”,               u” — u^, u.+ 1 = ' „ 1+1 + Sign(A+ 1) • „ 1+1.(43)

2          2                     2

Коэффициенты матрицы Л с полуцелыми индексами вычисляются по средним значениям параметров в соседних ячейках. Функция sign(Л) вычисляется через разложение

Л = RAR-1  ^  sign(Л) = Rsign(^) Д-1,(44)

где R и A — матрица собственных векторов и диагональная матрица собственных чисел матрицы Л, sign(A) = diag(sign( A 1 ),..., sign( A ^ )). Разложение (44) для (41) выглядит следующим образом:

Л =

1      1

с ²      0

с

—с р ¹ 0

с р

v — с 00

0    v0

0   0  v +

0    2 с - ² — 2 р с ^{- 1}

1  —с ^{- 2} 0

0    2 с ^{- 2} I р с ^{- 1}

где квадрат скорости звука с ² = Y P/ р .

Для устойчивости явной схемы (42) необходимо соблюдать ограничение на шаг интегрирования по времени. За шаг τ волны Римана, распространяющиеся со скоростями, равными собственным числам матрицы Л, не должны проходить расстояние больше размера ячейки. Отсюда вытекает соотношение т = v- min(-—.-----),

• Ы + с/’ где коэффициент ν, называемый числом Куранта — Фридрихса — Леви (CFL), должен быть меньше единицы (v < 1). В таком виде схема (42) имеет 1-й порядок аппроксимации.

Для записи схемы 3-го порядка введем обозначения для разностей

^{A u} i = ^u ” ^{— u} ” - ! .

Этап 1.

u^ = u” + R( ^-E — --A) £(R-1Aui,R-1Aui+1) ,(48)

где матрицы R, A и R ^{- 1} разложения (45) вычисляются на u ” .

Этап 2.

v- = u” + R( — 2e — 2-A) C(R-1Au-,R-1Au-+1) , v+ = u” + R( + |e — 2-A) £(R-1AU+, R-1Au++1) , здесь матрицы R, A и R-1 вычисляются соответственно на u- и на U+

Этап 3.

W • — w ”    f ( u 1+ 1 )    f ( u 1 - 1 ) L +       2          2   = 0, т              n

где

u 1+ 2 = ^( v 1+ , v 1+1 )

Этап 4.

»+1   »     дг _ дг. , W —W +   ,+ 2 -   •- 2 = 0,                      (52) т             h 1 1 ^ •+ 1 = 24(J - - ^ - )( и • — и - ) — 24(^ -+1 - J - )( u - +i — и - ).               (53)

Здесь матрица производных J от потоков системы (38) по переменным и = ( р , р, v)

имеет вид

v     0           р J = v 2      1          2 p v        .                       (54) , 2 v 3 Y— i v    Y— i P + 2 P v 2 -

Тестирование изложенного метода в работе [4] подтвердило 3-й порядок точности по пространству и времени.

На рисунке 3 представлены результаты расчетов изложенным методом для стандартного теста [16] c лимитерами (35) и (37). Начальные условия на отрезке [0,1] представляют собой разрыв в точке ж = 0,41 с исходными данными

( p L ,P l ,v l ) = (8, 10, 0), ( р д ,p r ,v r ) = (1, 1, 0), y = 1,4.

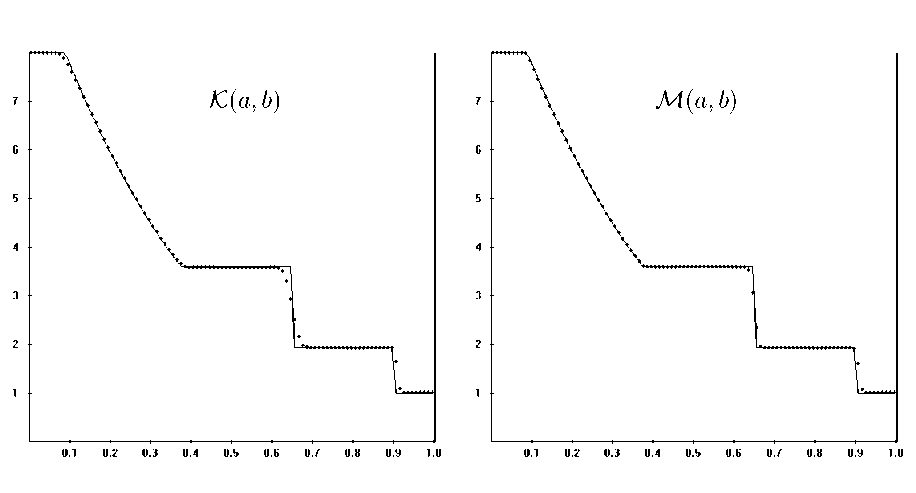
Рис. 3. Сравнение численных решений с разными лимитерами (35) и (37) для теста Сода.

Сетка из 100 ячеек на отрезке [0,1] , CFL=0,6. Результаты для плотности р(ж) показаны на момент времени t = 0, 27

Расчеты проводились на сетке из 100 ячеек с числом Куранта в (46) v = 0,6. Результаты для плотности р(ж) показаны на момент времени t = 0,27. Для правого варианта на рисунке 3 лимитер М(а,Ь) использовался только для первой и второй компоненты вектора характеристических разностей Д-1Аи в формулах (48)-(50). Тем самым его действие проявлялось в волне разрежения и контактном разрыве. Видно, что при использовании M(a,b) точность локализации контактного разрыва и границ волны разрежения существенно выше, причем признаки каких-либо численных флуктуаций отсутствуют. Разные лимитеры для разных характеристических полей успешно использовались в [5] для двухфазных течений. На целесообразность такого подхода впервые указано в [7].

В заключение параграфа отметим, что способ решения задачи Римана (точное решение или приближенное) заметного влияния на порядок аппроксимации метода не оказывал. В то же время замена функции лимитера на более простой кусочно-линейный ограничитель minmod приводила к тому, что порядок аппроксимации метода снижался до второго.

Заключение

Предложено семейство гладких нелинейных адаптивных лимитеров, основанных на лимитере центральных разностей. Показано, что их использование существенно улучшает точность решения в окрестности разрывов первых производных и локальных экстремумов. Доказана теорема о том, что модификация метода Годунова 3-го порядка [4] с этими лимитерами обладает TVD-свойством. Представлена экономичная версия метода для уравнений газовой динамики с квадратичной реконструкцией параметров в трациционных переменных. Метод имеет 3-й порядок аппроксимации по пространству и времени и является развитием W-метода 2-го порядка [1] за счет подключения двух отдельных блоков коррекции. Предложенный подход построения разностных схем 3-го порядка может быть использован для неоднородных и двумерных гиперболических систем нелинейных уравнений.