Учебно-методическое обеспечение по дисциплине «Теоретические основы начального курса математики»

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 372.851                                        

Учебно-методическое обеспечение как педагогическая проблема в теории и методике профессионального образования определяется как одно из ведущих научных направлений. Ряд фундаментальных исследований психологов [11], дидактов и методистов [9] посвящен проблеме развития теоретических основ средств обучения. В психолого-педагогических исследованиях освещаются различные стороны проблемы создания и использования форм учебно-методического обеспечения. Решается она в аспекте активизации процесса обучения и рациональной организации самостоятельной работы студентов с использованием учебнометодической литературы; формирования мотивации студентов в профессиональном саморазвитии; разработки модели активной профессиональной самоподготовки студентов; моделирования содержания учебного материала на основе проблемно-модульного обучения [2–7]. Для эффективного развития профессионального образования ряд исследователей предлагают более полно реализовать личностный подход, позволяющий создавать условия для индивидуального проявления, развития и самореализации студентов, обеспечивать им свободу выбора в обучении, способствовать реализации каждым из них личностных притязаний и способностей [1]. На основе структурно-функционального анализа деятельности преподавателя и системного подхода к процессу обучения разработана модель методического обеспечения, структура учебно-методического комплекса по учебной дисциплине ТОНКМ в колледже [2]. В этой модели будет изучено взаимосвязанные подсистемы педагогической системы. Они могут включать в себя: I. Цель образования. II. Содержание образования. III. Дидактические процессы. IV. Организационные формы [3].

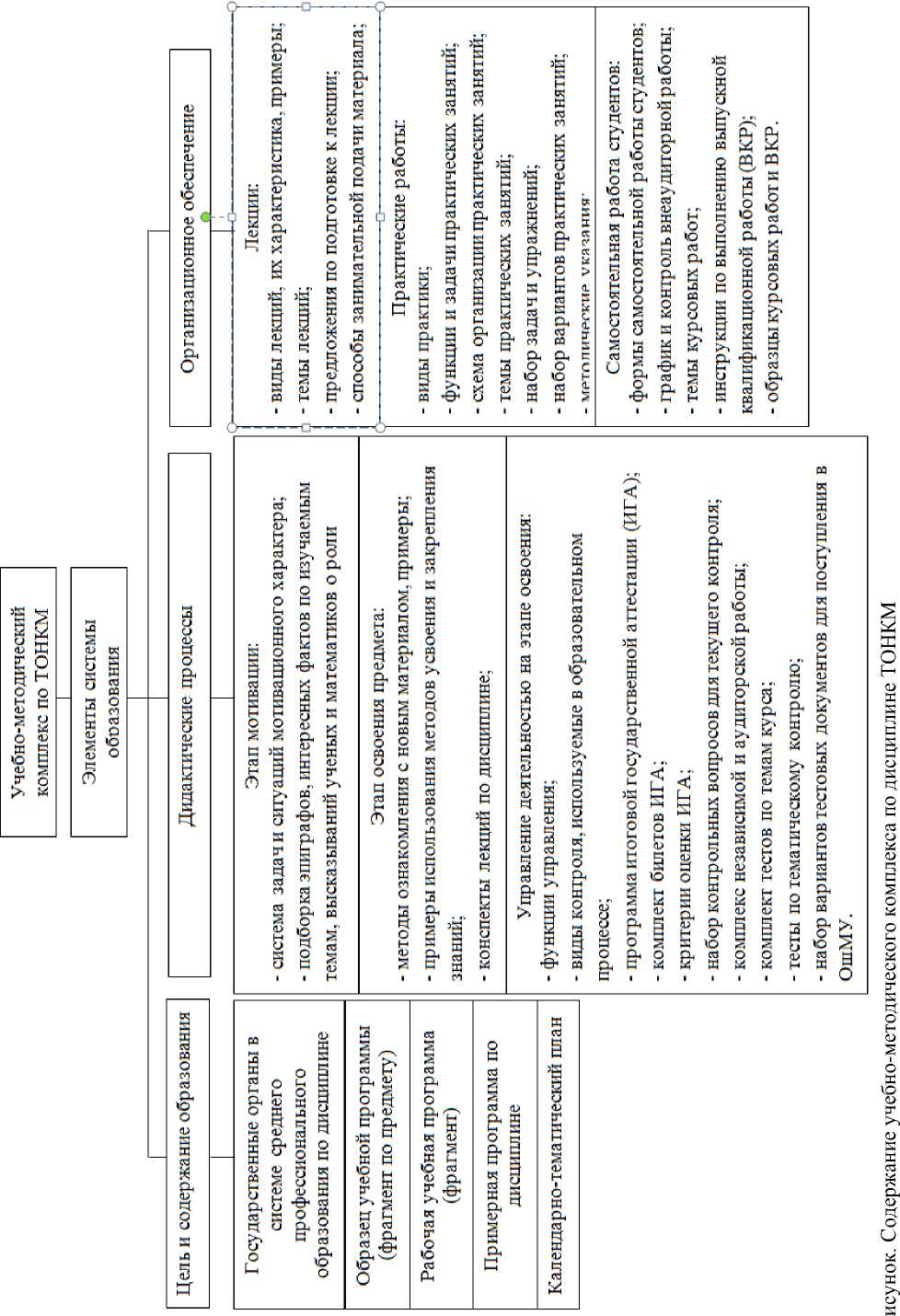
Компонентный состав учебно-методического комплекса по дисциплине ТОНКМ, разработанного автором данного исследования, систематизирован в виде описательной схемы по ее структуре (Рисунок). Кроме того, педагог начальной школы должен стимулировать учащихся к самостоятельной творческой работе, ознакомить их с различной периодической литературой, образцами творческих работ студентов из предыдущих выпусков. Для этой цели также целесообразно прибегать к нетрадиционным формам уроков: КВН, уроки с соревновательным характером, «путешествия» в мир математики и т.д [4].

Одним из лучших качеств учителей начальных классов является умение анализировать полученные знания учеников по математике и вызвать у них интерес к предмету. Наряду с этим, важное значение имеет профессионально ориентированное обучение, не только в занятиях специальных методических курсов, но и по всем предметам, в том числе, и по математике [5].

В связи с этим преподавание курса математики в педагогических колледжах должно представлять собой сочетание теоретических и методических концепций [8]. Анализ опыт работы в этом направлении показывают, что профессионально-педагогическая ориентация в обучении математике будущих педагогов начальной школы может быть успешно осуществлена при выполнении следующих условий: мотивации к различным видам профессии, предполагающим использование математики; ориентации методов и форм обучения математике на подготовку студента к будущей практической работе педагога; ориентации всей классной, внеклассной и исследовательской работы со студентами на практические нужды и навыки. Рассмотрим подробнее содержание первого из приведенных выше условий.

Мотивация к изучению курса ТОНКМ . Для достижения этой цели были выдвинуты идеи связать этот курс в колледже с курсом математики в начальной школе. В этом направлении можно успешно создать научные основы начального курса математики. Опыт показывает, что при целенаправленном и систематическом использовании школьных учебников усвоение учащимися основных понятий курса становится более осмысленным и информативным. Рассмотрим классификацию мотивационных методов.

• 1.    Вербальные мнения о необходимости изучения данной темы в связи с будущей профессиональной деятельностью. Например, тема: «Элементы логики». «Чтобы освоить систему понятий, предложений и доказательств и затем успешно использовать полученные знания и умения, решить задачу обучения младших школьников и их развития с помощью математики, необходимо сначала разобраться в определениях и предложениях, выражающих сами свойства этих понятий и доказательств».

• 2.    Обоснование практической значимости проблемы — предмета дальнейших исследований. Например, тема: «Элементы логики». «Изучение этого материала связано с овладением теоретико-множественным языком, который используется не только при рассмотрении логической структуры математических понятий, предложений и доказательств, но и при создании всего курса» [6].

• 3.    Разъяснение учащимся логики изучения проблемы с точки зрения профессиональной деятельности и их математического образования. Например, тема: «Теоретикомножественное значение натурального числа, нуля и операций над числами». Введя понятие отрезка натурального ряда, мы установили, что подсчет элементов конечного множества приводит к счетному числу. Используя теоретико-множественные концепции, можно объяснить значение натурального числа, не связывая его со счетом [5]. Мы делаем это в рамках так называемого теоретико-множественного подхода к числу. Знание этого метода поможет учителю начальной школы понять, как построены те курсы начальной математики, в основе которых лежит сложная теоретико-множественная модель системы натуральных чисел, используемая явно или неявно [5].

• 4.    Использование конкретных ситуаций, связанных с содержанием начального курса математики. Например, тема: «Умозаключения и их виды». «Давайте посмотрим на некоторые примеры умозаключений, которыми руководствуются школьники младших классов при изучении математики. Ученику предлагается объяснить, почему число 23 можно выразить в виде суммы 20 + 3. Он говорит: «Число 23 состоит из двух цифр. Любое

• 5.    Использование исторического материала. Например, тема: «Натуральные числа и ноль». «Теоретическая наука, которая стала изучать числа и действия над ними, называлась «арифметикой». Слово «арифметика» происходит от греческого слова arithmos, что означает «число». Следовательно, арифметика есть наука о числах» [7].

• 6.    Использование опыта и знаний учащихся по курсам средней школы. Например, тема: «Неравенства с одной переменной». «Урок на тему можно начать с вовлечения учащихся в знание следующих выражений из курса математики: 3х – 6 < 9х + 2; х² + 5х – 7 > 0; (8x + 3)(6 – 5x) < 0 называются неравенствами с одной переменной. Решаем неравенства, обращаемся к определениям «неравенство с одной переменной» и «эквивалентные неравенства», создаем и доказываем теоремы об эквивалентности неравенств» [8].

• 7.    Математическое объяснение задач из учебников для начальных классов. Например, тема: «Сообщения и формы уведомлений». «Покажите, что выполнение учащимися начальных классов следующих задач связано с понятием формы выражения, сферой ее определения и заданным множеством истинности:

двузначное число можно представить в виде суммы двух чисел разных разрядов. Следовательно, 23 = 20 + 3».

• 1)    Из чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, выделите делящиеся на 3.

• 2)    Назовите все числа меньше 7 (только целые неотрицательные числа)» [9].

• 8.    Информация о содержании курса математики в начальной школе. Например, тема: «Математические понятия». «Среди понятий, изучаемых в элементарном курсе математики, имеют место такие, как «треугольник», «многоугольник», «прямой угол», «число», «четное число», «трехзначное число», «слагаемые», «сумма», «выражение». Имеются ли среди них есть понятия, связанные с: 1) родом и видом; 2) целым и частью» [10]. Сформулированные методы мотивации учебной деятельности учащихся характеризуют профессиональную направленность курса математики [11]. Они играют важную роль в процессе подготовки учителей начальной школы. Однако, на наш взгляд, данная система методов мотивации в содержании учебника не является всеобъемлющим и не в полной мере решает современные проблемы мотивации обучения, большинство методов информативны, и только, и не содержат проблемных элементов. С этой целью нами разработаны другие методы повышения эффективности обучения студентов, активизации их мотивации и формированию у них познавательной деятельности. Эти способы практически апробированы в процессе обучения.

• 1.    Передача успеха. Передача успеха является важным ресурсом при создании условий для мотивации учащихся. Необходимо поддерживать развитие успехов, недостатки, обычно, замедляют процесс обучения. Студенты, ориентированные на успех, успевают лучше, чем учащиеся, чья мотивация, в основном, сводится к избеганию от неудач. Чрезмерные требования приводят к неудовлетворенности из-за их чрезмерно высокого уровня. В то же время, слишком низкий уровень требований приводит к скуке. Советы для повышения мотивации: положительный отзыв в отношении обучающихся (поощрение); предложение примеров средней сложности; наглядное представление успехов обучающихся даже после частичного достижения целей (тесты и упражнения без оценок, работа в группах со сравнением результатов); постепенное повышение уровня сложности (переход от простых задач к сложным, переход от групповой работы к самостоятельной работе); четкое изложение.

• 2.    Примеры из практики. Рекомендации: использовать опыт педагогической практики; личные примеры из практики; метод проектов; итоговые занятия приближенные к практике; лекции приглашенных практиков.

• 3.    Образы действий, вызывающие интерес. Мотивация возрастает, когда вы начинаете новое и увлекательное занятие. «Готовые» решения и игнорирование решений, самостоятельно принятых обучающимися, убивают интерес и приводят к снижению мотивации. Предложения: не предлагать готовые решения; дать возможность проводить самостоятельные эксперименты; использование методов соревнования в игровой форме; работа над проектами; методологические последствия неожиданных действий, например, через противоречивые взгляды; ссылки на литературу, в особенности, с различными подходами.

• 4.    Участие в работе над проблемой. Рекомендации: постоянно прерываать лекции упражнениями (меняющиеся модели рецептивной и продуктивной деятельности); работать в небольших группах над решением проблемы; этапы обсуждения; обобщение вкладов студентов; вовлечение студентов в проекты; практическая деятельность.

• 5.    Свобода действий при принятии решений. Советы: случайный выбор студентами практических примеров; свободный выбор тем выпускных работ; принятие совместных решений по теме основных задач.

• 6.    Связь с другими областями знаний. Предложения: проектное обучение; междисциплинарная разработка личных тем; интегрированный урок; приглашение отдельных коллег на специальные мероприятия.

• 7.    Обзор перед детальной презентацией. Рекомендации: предоставление плана учебных занятий; объяснять программу семестра на первых занятиях; соответстенно в начале и в конце урока дается обзор глав и выводы.

• 8.    Разъяснение целей обучения. Предложения: сформулировать цели обучения перед каждым разделом; предоставить возможность определить цели обучения на конкретных примерах; предоставить возможность определить практическую значимость и жизнеспособность цели и т. д.

На основе образовательной программы подготовки учителей начальных классов определены возможные пути реализации учебно-методического комплекса по дисциплине «Теоретические основы начального курса математики». Установлена модель, структура и содержание учебно-методического комплекса по дисциплине ТОНКМ в колледже.