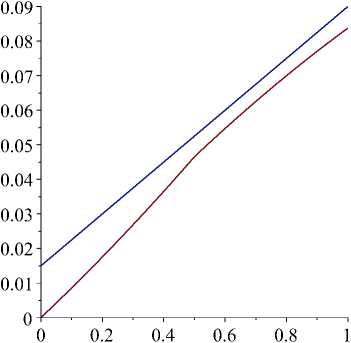
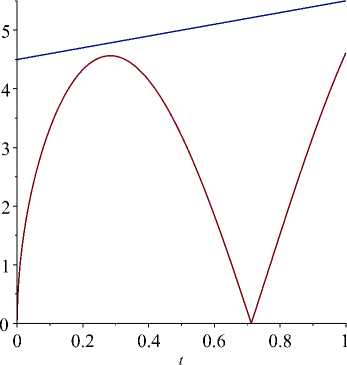
Ulam-Hyers stability of four-point boundary value problem for Caputo fractional differential equations with a parameter

Ulam-Hyers stability of four-point boundary value problem for Caputo fractional differential equations with a parameter

Автор: Castro Luis Filipe Pinheiro, Silva Anabela De Sousa

Журнал: Владикавказский математический журнал @vmj-ru

Статья в выпуске: 4 т.24, 2022 года.

Бесплатный доступ

Fractional calculus is considered to be a powerful tool in describing complex systems with a wide range of applicability in many fields of science and engineering. The behavior of many systems can be described by using fractional differential equations with boundary conditions. In this sense, the study on the stability of fractional boundary value problems is of high importance. The main goal of this paper is to investigate the Ulam-Hyers stability and Ulam-Hyers-Rassias stability of a class of fractional four-point boundary value problem involving Caputo derivative and with a given parameter. By using contraction principles, sufficient conditions are obtained to guarantee the uniqueness of solution. Therefore, we obtain sufficient conditions for the stability of that class of nonlinear fractional boundary value problems on the space of continuous functions. The presented results improve and extend some previous research. Finally, we construct some examples to illustrate the theoretical results.

Еще

Fractional boundary value problem, caputo derivative, ulam-hyers stability, ulam-hyers-rassias stability

Короткий адрес: https://sciup.org/143179312

IDR: 143179312   |   DOI: 10.46698/v3243-1645-4815-b

Список литературы Ulam-Hyers stability of four-point boundary value problem for Caputo fractional differential equations with a parameter

  • Oldham, K. B. Fractional Differential Equations in Electrochemistry, Advances in Engineering Software, 2010, vol. 41, no. 1, pp. 9–12. DOI: 10.1016/j.advengsoft.2008.12.012.
  • Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering, New York, Academic Press, 1999.
  • Samko, S. G., Kilbas, A. A. and Marichev, O. I. Fractional Integrals and Derivatives: Theory and Applications, Singapore, Gordon & Breach, 1993.
  • Torvik, P. J. and Bagley, R-L. On the Appearance of Fractional Derivatives in the Behavior of Real Materials, Journal of Applied Mechanics, 1984, vol. 51, no. 2, pp. 294–298. DOI: 10.1115/1.3167615.
  • Kilbas, A. A., Srivastava, H. M. and Trujillo, J. J. Theory and Applications of Fractional Differential Equations, Amsterdam, Netherlands, Elsevier, 2016.
  • Yang, C. and Zhai, C. Uniqueness of Positive Solutions for a Fractional Differential Equation Via a Fixed Point Theorem of a Sum Operator, Electronic Journal of Differential Equations, 2021, vol. 70, pp. 1–8.
  • Wang, C. and Xu, T.-Z. Stability of the Nonlinear Fractional Differential Equations with the Right-Sided Riemann–Liouville Fractional Derivative, Discrete and Continuous Dynamical Systems. Ser. S, 2017, vol. 10, no. 3, pp. 505–521.
  • Zhai, C. and Hao, M. Fixed Point Theorems for Mixed Monotone Operators with Perturbation and Applications to Fractional Differential Equation Boundary Value Problems, Nonlinear Analysis: Theory, Methods & Applications, 2012, vol. 75, no. 4, pp. 2542–2551. DOI: 10.1016/j.na.2011.10.048.
  • Zhai, C. and Xu, L. Properties of Positive Solutions to a Class of Four-Point Boundary Value Problem of Caputo Fractional Differential Equations with a Parameter, Communications in Nonlinear Science and Numerical Simulation, 2014, vol. 19, no. 8, pp. 2820–2827. DOI: 10.1016/j.cnsns.2014.01.003.
  • Zhai, C., Yan, W. and Yang, C. A Sum Operator Method for the Existence and Uniqueness of Positive Solutions to Riemann–Liouville Fractional Differential Equation Boundary Value Problems, Communications in Nonlinear Science and Numerical Simulation, 2013, vol. 18, no. 4, pp. 858–866. DOI: 10.1016/j.cnsns.2012.08.037.
  • Zhao, X., Chai, C. and Ge, W. Positive Solutions for Fractional Four-Point Boundary Value Problems, Communications in Nonlinear Science and Numerical Simulation, 2011, vol. 16, no. 9, pp. 3665–3672. DOI: 10.1016/j.cnsns.2011.01.002.
  • Ulam, S. M. Problems in Modern Mathematics, New York, John Wiley & Sons, 1940.
  • Hyers, D. H. On the Stability of the Linear Functional Equation, The National Academy of Sciences USA, 1941, vol. 27, pp. 222–224.
  • Rassias, T. M. On the Stability of the Linear Mapping in Banach Spaces, Proceedings of the American Mathematical Society, 1978, vol. 72, no. 2, pp. 297–300. DOI: 10.1090/S0002-9939-1978-0507327-1.
  • Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications, Elsevier, 1998.
  • Wang, J., Lv, L. and Zhou, Y. Ulam Stability and Data Dependence for Fractional Differential Equations with Caputo Derivative, Electronic Journal of Qualitative Theory of Differential Equations, 2011, no. 63, pp. 1–10. DOI: 10.14232/ejqtde.2011.1.63.
  • Ali, A., Shah, K. and Li, Y. Topological Degree Theory and Ulam’s Stability Analysis of a Boundary Value Problem of Fractional Differential Equations, Frontiers in Functional Equations and Analytic Inequalities, Springer, Anastassiou G., Rassias J. (eds), 2019, pp. 73–92. DOI: 10.1007/978-3-030-28950-8_4.
  • Ali, A. and Shah, K. Ulam–Hyers Stability Analysis of a Three-Point Boundary-Value Problem for Fractional Differential Equations, Ukrainian Mathematical Journal, 2020, vol. 72, no. 2, pp. 161–176. DOI: 10.1007/s11253-020-01773-2.
  • Ali, A., Shah, K. and Abdeljawad, T. Study of Implicit Delay Fractional Differential Equations under Anti-Periodic Boundary Conditions, Advances in Difference Equations, 2020, vol. 2020, Article no. 139, pp. 1–16. DOI: 10.1186/s13662-020-02597-x.
  • Dai, Q., Gao, R., Li, Z. and Wang, C. Stability of Ulam–Hyers and Ulam–Hyers–Rassias for a Class of Fractional Differential Equations, Advances in Difference Equations, 2020, vol. 2020, Article no. 103, pp. 1–15. DOI: 10.1186/s13662-020-02558-4.
  • Palaniappan, M. Hyers–Ulam–Rassias Stability of Nonlinear Fractional Differential Equation with Three Point Integral Boundary Conditions, International Journal of Engineering Research and Technology, 2020, vol. 13, no. 12, pp. 4679–4685.
  • El-hady, E. and ¨O˘grek¸ci, S. On Hyers–Ulam–Rassias Stability of Fractional Differential Equations with Caputo Derivative, Journal of Mathematics and Computer Science, 2021, vol. 22, no. 4, pp. 325–332. DOI: 10.22436/jmcs.022.04.02.
  • Gronwall, T. H. Note on the Derivatives with Respect to a Parameter of the Solutions of a System of Differential Equations, Annals of Mathematics, 1919, vol. 20, no. 4, pp. 292–296. DOI: 10.2307/1967124.
  • Bellman, R. The Stability of Solutions of Linear Differential Equations, Duke Mathematical Journal, 1943, vol. 10, no. 4, pp. 643–647. DOI: 10.1215/S0012-7094-43-01059-2.
Еще
Статья научная
SciUp 2024 © 2024 ©