Управление качеством подготовки специалистов

Quality management for preparing specialists

The authors of the following article consider that the given approach presented in this work can serve as a basis for development theoretical and applied models of quality management system for preparing specialists as well as for creation models for other management systems.

азработка модели подготовки специалистов с высокими профессиональными, психофизиологическими, социальными и иными качествами (ориентированная на создание соответствующего алгоритма с его последующим воплощением в программный продукт) предполагает:

• —    введение системы численных показателей, с необходимой полнотой характеризующих индивидуальные качества специалиста (обучаемого), и их анализ в динамике развития;

• —    введение системы численных показателей, с необходимой полнотой характеризующих качество процесса подготовки специалистов в учебном заведении (от конкурсного отбора абитуриентов до вручения каждому выпускнику документов об окончании учебного заведения, среди которых будет документ, содержащий показатели качества выпускника) [1, 2];

• —    определение взаимосвязи между показателями качества каждого отдельно взятого обучаемого и показателями процесса подготовки специалистов в учебном заведении;

• —    установление функциональной зависимости показателей процесса подготовки специалистов от управляющих воздействий (управления) со стороны управленческих структур учебного заведения.

Перечисленные задачи служат концептуальным описанием модели управления качеством подготовки специалистов. Действительно, сравнение специалистов (обучаемых) между собой и с «эталонными» представлениями об уровне их подготовки (в связи с профессиональным прогностическим отбором и т. п.) возможно лишь тогда, когда имеются способы численной оценки свойств, которыми должен обладать специалист данной профессии (обучае-

мый). Это же утверждение относится и к сравнению между собой (и с «эталонами») систем подготовки специалистов, систем управления подготовкой специалистов в различных учебных заведениях, а также к учебным заведениям в целом.

Введение указанных количественных показателей вместе с установлением их зависимости от качественных и количественных характеристик управления позволит сформулировать и решить задачу наиболее эффективного управления подготовкой специалистов максимально высокого качества [1, 3] (в рамках модели управляющее воздействие, которое характеризуется набором своих численных показателей, приводит к контролируемому изменению показателей качества специалиста; это относится, например, и к отбору абитуриентов). Такой модельный подход означает рассмотрение учебного процесса как технологического процесса в «индустрии» подготовки специалистов.

Качество специалиста (обучаемого) — это многофакторная характеристика, причем каждая профессия предъявляет свои требования к каждому из факторов качества личности специалиста. Все факторы должны иметь численное выражение и всегда могут быть введены по принципу: чем выше качество, тем больше фактор. Указанные факторы разнородны, меняются с течением времен t , и, очевидно, было бы неправильно сворачивать их в один показатель качества специалиста.

Таким образом, качество каждого отдельно взятого специалиста данной профессии может быть описано вектором Q(t), что позволяет говорить о «направлении» и «уровне» развития личности специалиста (или профессии). Требования к качеству подготовки специалис- та можно сформулировать в виде условного неравенства:

I                                               I

^Q(t) >  Q min (t),             (1)

где Qmin(t) — вектор качества, координаты которого составлены из минимально допустимых факторов качества. Неравенство означает, что каждая координата вектора Q(t) должна быть не меньше соответствующей координаты век-^а тора e„„(t)

Учебный процесс, как технология подготовки специалиста данной профессии, а также профессиональная деятельность специалиста на протяжении любого периода времени t e [t_r t₂] должны быть охарактеризованы упорядоченным набором показателей качества (учебного процесса либо условий профессиональной деятельности), имеющих численное значение и подлежащих по своему существу максимизации. Этот набор представляет собой вектор q(t) , отражающий качественный уровень организации учебного процесса в данном учебном заведении (уровень организации профессиональной деятельности). Требования к уровню организации учебного процесса (профессиональной деятельности) будут выражаться неравенством, аналогичным неравенству (1):

^q(t) >  ^q mJ I).              (2)

где q_min(t) — вектор минимально допустимого (по каждому из показателей) качества организации учебного процесса (профессиональной деятельности). Далее будем говорить только об учебном процессе.

Качество специалиста (обучаемого) Q(t) в момент времени t определяется качеством q( т ) учебного процесса на всем предшествующем интервале времени те [t₁, t₂], а также условиями существования и развития личности до поступления в учебное заведение т <  t₀. Вместе с тем ясно, что усвоение учебного материала в текущий момент времени т зависит от свойств Q( т ) личности в этот момент времени. Поэтому вектор Q(t) качества специалиста (обучаемого) является функционалом вектор-функции q( т ) качества учебного процесса и вектор-функции Q( т ) . Предложим для выражения указанной зависимости при т >  t₀ интегральное соотношение:

t ^а           ^а                 ^а                  ^а

Q(t) = Q(t o ) + J F( i ,< a ( т ),QJ)) • d i ,    (3)

to где F (т,((т),Q(т)) — некоторая вектор-функ ция указанных переменных, отражающая становление специалиста в ходе учебного процесса и подлежащая определению. Вектор-функционал (3) демонстрирует очевидный факт: чем выше подготовка абитуриента, задаваемая вектором Q(t0), тем выше при прочих равных условиях качество выпускника.

Управление учебным заведением (системой) можно разделить на тактическое (реализующее установленные функции управляющей системы) и стратегическое (направленное на введение/ удаление структурных подразделений и/или изменение их функциональных обязанностей). Конструктивное управление должно быть направлено на улучшение работы системы (на увеличение показателей ее работы) и может быть вызвано внешними и внутренними причинами. Управление является, вообще говоря, комплексным (многомерным) действием, имеющим некоторое распределение во времени. Поэтому с математической точки зрения управление следует рассматривать как вектор u (t) . Для краткости среди аргументов u (t) неприводим величины, отражающие причины и параметры управления (в том числе опускаем вектор Q(t). Управление учебным процессом в период времени 9 < т оказывает непосредственное влияние лишь на вектор q ( т ) качества учебного процесса:

q( т ) = J f ( 9 ,u( 9 )) • d 9 , (4) где f ( 9 ,u( 9 )) — вектор-функция, которая описывает влияние управления на показатели учебного процесса и подлежит определению.

Вектор-функция f( 9 ,u( 9 )) определяет задержку между управляющим воздействием и соответствующим изменением показателей учебного процесса, и для каждого учебного заведения имеет в общем случае свой вид (задаваемый, прежде всего, типом учебного заведения).

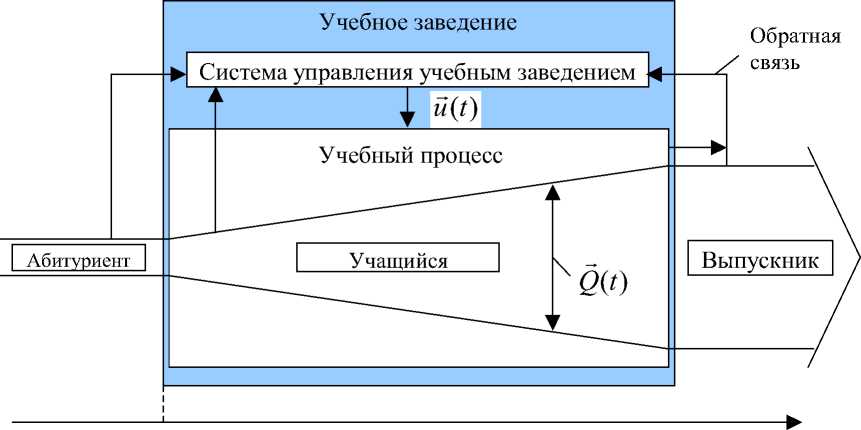
Вектор-функционалы (3), (4) являются математическим воплощением модели управления качеством подготовки специалистов (образно представленной на рис.) и демонстрируют высокую алгоритмическую сложность поставленной задачи.

Интегральным выражениям (3), (4) эквивалентна система векторных дифференциальных уравнений (при учете всех необходимых факторов и введении начальных условий таких, как ^а ^а

Qo = Q(to) ит.п.): ^а dQ^ = F (t,q (t),Q (t)), <Э d t

t0                                                                             t

Модель управления качеством подготовки специалистов dqp)=f (в,в (в)). (6) dt

Следующие этапы исследований должны быть направлены на установление вида вектор-функций q(t) , QB(t) , B(t) , F(t,q,Q) и f⁽t, ^B ) Поиск оптимального управления ^в ( в ) качеством на некотором промежутке времени в е [ т ₀, т ] должен осуществляться в результате решения одной из следующих оптимизационных задач:

I

Q(t ,B ( в )) ^ max, в ( в )

в в

Q(t,B( в )) ^ Q_op t , (₈) где Q_opt — заданный вектор качества. Векторный критерий (7) должен пониматься как система критериев, в которых максимизируется каждая координата вектора Q . Критерий (7) представляет собой традиционную задачу системного анализа, в которой искомое решение должно принадлежать множеству Парето-опти-мальных решений [4].

Поскольку своевременное улучшение качества q учебного процесса должно приводить к повышению качества Q подготовки специалистов (во всяком случае, не может быть обратного), задача (7) сводится к задаче оптимального управления элементами учебного процесса [1, 3] (а при определенных условиях тождественна этой задаче):

q(t,Bl.( в )) ^ max. в ( в )

Конечно же, задачи (7) и (9) существенно упростятся, если будет предложен корректный, всесторонне обоснованный способ свертки векторных показателей Q и q в соответствующие скалярные показатели, после чего векторные критерии (7) и (9) примут скалярную форму.

Отметим также, что подынтегральные век-тор-функции F и f из выражений (3), (4) для некоторых моделей управления, возможно, будут содержать своих аргументов соответственно моменты времени t и т , совпадающие с верхними пределами интегрирования в (3) и (4). Это приведет к адекватным изменениям уравнений (5) и (6).

Изложенный в настоящей работе подход может служить основой для разработки теоретических и прикладных моделей систем управления качеством подготовки специалистов, а также для создания моделей других систем управления.