Управление с "поводырем" двухзвенным манипулятором с вращательными парами
Автор: Лутманов С.В., Попова Е.С.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 4 (27), 2014 года.
Бесплатный доступ
Решается игровая задача управления о переводе схвата манипулятора на базовую траекторию движения в предположении, что измерение фазового вектора игры производится с некоторой погрешностью. Численно подтверждено, что процедура управления с "поводырем" является эффективным средством управления конфликтно-управляемым динамическим объектом в условиях неточного измерения фазового вектора дифференциальной игры.
Манипулятор, математическая модель, дифференциальная игра, управление с "поводырем"
Короткий адрес: https://sciup.org/14729943
IDR: 14729943 | УДК: 519.7
Текст научной статьи Управление с "поводырем" двухзвенным манипулятором с вращательными парами
На горизонтальной плоскости рассматривается двухзвенный механический манипулятор с двумя вращательными парами (рис. 1), управление которым осуществляется моментами, развиваемыми в соединительных парах. Задана траектория схвата и его закон движения вдоль этой траектории. Указанный закон движения реализуется посредством известных программных управлений. В случае, когда начальные условия для схвата нарушаются, его дальнейшее движение будет отклоняться от базового.
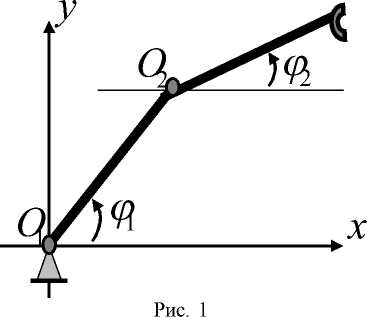
Возвращение схвата на базовую траекторию осуществляется посредством применения дополнительных управлений. В предположении, что нарушения начальных условий незначительны, задача о возращении схвата на базовую траекторию сводится к задаче приведения фазового вектора линеаризованной модели в начало координат. Линеаризация производится в окрестности базового закона движения. В работе [2] эта задача была решена в предположении, что в соединительных парах могут возникать неконтролируемые помехи в виде вращательных моментов. Неконтролируемой помехе предписывалось стремление максимально навредить в решении задачи перевода схвата на базовую траекторию. На дополнительные управления и вращательные моменты, развиваемые неконтролируемой помехой, накладывались геометрические ограничения в виде выпуклых компактных множеств.
В данной статье допускается, что измерение фазового вектора линеаризованной модели производится неточно. Известно [3], что в этих условиях оптимальная стратегия управления, реализованная в форме прицеливания на соответствующий стабильный мост, является неустойчивой по отношению к ошибке измерения фазового вектора. В данной статье оптимальное управление манипулятором осуществляется в виде процедуры управления с " поводырем " [1], преодолевающей этот недостаток.
-
1 . Линеаризованная модель
Манипулятор представляет собой механизм с двумя степенями свободы. Пусть qw. q0: [0,1]^ R4 закон движения, манипу лятора, порожденный управлением w* (•) и 0
выходящий из начального положения q , а qw• q0* : [0,1] ^ R4 - выходящий из начального положения q °*. Полагаем x ( t ) qw** ,q0* ( t ) qw**,q0 (t ) , t e[0,1] .
Предполагается, что величина ||q °*- q 0|| мала. Дифференциальные уравнения линеаризованной модели имеют вид [2]
x _ A ( t ) x + B ( t ) ( u + v ) , (1.1)
Q _ bw 1 — bcq 4 2 sin( q 1 — q 2 )
-
3 ab — c 2cos2( q 1 — q 2 )
—
cw2 cos( q 1 — q 2 ) ab — c 2 cos2 ( q 1 — q 2 ) 1 c2 q 32sin[2( q 1 — q 2 )] -
2 ab — c2cos2(q 1 — q2)
q aw2 + acq 32 sin( q 1 — q 2)
-
4 ab — c 2cos2( q 1 — q 2)
—
c w 1 cos( q 1 — q 2 ) ,
2------2+ ab — c cos (q1 — q2)
, 1 c2 q 4 2sin[2( q 1 — q 2 )]
+— •------;----;---------
2 ab — c 2cos2( q 1 — q 2) ,
Здесь u e R2 - вектор дополнительных управляющих параметров, а v e R2 - вектор
где
A (t)
_ d Q ( t , q , u )
d q
управляющих параметров помех. При этом
u e P _«
f 0
fF 1
P q 2 )
fF 1
P q 2 )
*
*
B (t)
q _ q * 0 w , q
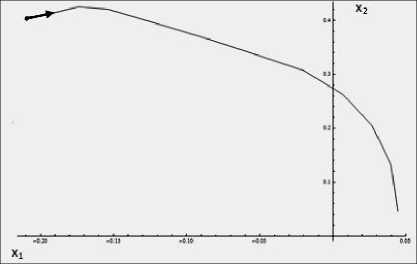
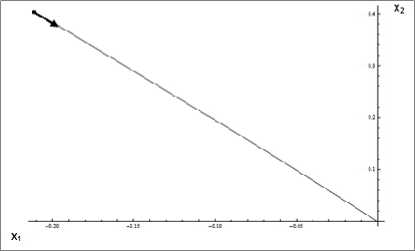
f> 1 p 1 ld q з) * * (t), w=w •( t) p 1Id q 4) p Q4 1 * * ld q 4)) V eQ _< fV11 P v 2 ) [ u’1 < u 2 ) 22 2 u1 + u2< a 1, V’2+ v 22 < в21, a > в > 0. _ d Q (t, q, w) 5 w f 0 0 P Q3 1 * 0 (t), w=w • 0 1 0 11 fd Q3 1* q_q . t w ,q '•( t) \ d w1 ) * d w1) P w2 ) * F P w2 ) ) , Задача возвращения схвата на базовую траекторию представляет собой антагонистическую дифференциальную игру наведения-уклонения, целевым множеством для которой служит начало координат. В этой игре первый игрок распоряжается управляющими параметрами u e P, а второй - параметрами v e Q. Первый игрок решает задачу наведения и поэтому является игроком-союзником. Свою оптимальную стратегию он строит в форме экстремального прицеливания на стабильный мост, обрывающийся в конечный момент на целевом множестве. Выше уже отмечалось, что такой способ управления является эффективным, если измерение фазового вектора игроком-союзником производится без погрешностей. В противном случае игрок-союзник должен применить процедуру управления с "поводырем". Q = f Q1 Q2 Q3 IQ4 ) , Q1 = q3, Q2 = q4, 2. Процедура управления с "поводырем" Предполагается, что в любой момент времени выполнено неравенство Ix (t)" x •( 11< Z Z a 0. где x*(t)- измеренное значение фазового вектора линеаризованной модели. Следуя [1] опишем позиционную процедуру управления с "поводырем". Пусть W - стабильный мост первого игрока в антагонистической дифференциальной игре с динамикой (1.1), обрывающийся в момент времени 5 g[0, T] в начале координат. Введем виртуальный динамический объект, который будем называть "поводырем". Его динамика описывается тем же дифференциальным уравнением (1.1), что и реальный объект. Для отличия фазовый вектор "поводыря" будем обозначать буквой w . Таким образом, w = A (t) w + B (t)(u + v), t g[ 10, T ] , w G Rn , u G P, v G Q. Рассмотрим разбиение Д промежутка времени [ 10,5] на полуинтервалы: К,Ts+1 ) , s = 0,1,^, k-1, Т 0 = t 0, тк = 5. Опишем действия первого игрока на каждом из указанных полуинтервалах (см. рис. 2). Рис. 2. Траектория "поводыря" Полуинтервал [т0,т1). Определяем точку w0на сечении моста как ближайшую к x *. Имеем IIx ’-М=.min,! x'-w • (2.1) где x * измеренное первым игроком в начальный момент времени t0положение фазового вектора. Управление u0 = const первого игрока на полуинтервале [т0,т1) находится из условия (z0, Bu °) = min (z0, Bu}, (2.2) ' 0 / u G P ' 0 ' где z0 = x* - w0. Если условия (2.1), (2.2) определяют вектор u0 g P неоднозначно, то берется любой из них. Движение реального динамического объекта получим интегрированием дифференциального уравнения x = A (t) x + B (t)(u 0 + v (•)), x (t J = x *, t g[t о, т1). Полагаем x1 = lim x (t). Движение пово-t ^T1 дыря w(•) отождествим с тем решением дифференциального уравнения в контингенциях w g A (t) x + B (t)(P + v0), w(t*) = w0, tG[T0,т1), ( z0, Bv0) = max (z0, Bv}, ' / v G q x ' для которого выполнено включение w(т1 )g W (т1). Такое решение существует по определению стабильного моста. Полагаем w1 = lim w (t). t ^т1 Полуинтервал [т1, т2). Пусть x1* - измеренное первым игроком в момент времени τ1положение фазового вектора. В общем случае w1 ^ x* . Управление u1 = const первого игрока на полуинтервале [т1, т 2) определяем из условия (z, Bu '\ = min (z,, Bu}, (2.3) \ 1 / u G P ' 1 где z1 = x* - w1. Если условие (2.3) определяет вектор u1g P неоднозначно, то берется любой из них. Движение реального динамического объекта получим интегрированием дифференциального уравнения x = A (t) x + B (t)(u1 + v (•)), x(т1 ) = x1, t G[т1, т2 ) . Полагаем x2= lim x (t). Движение "по-t ^т 2 водыря" w(•) отождествим с тем решением дифференциального уравнения в континген-циях w g A (t) x + B (t)(P + v1), w(т1 ) = w1, tG[то,т1), (Zj, Bv1) = max (zj, Bv}, ' ' vgq ' ' для которого выполнено включение w(т2 )e W (t2). Такое решение существует по определению стабильного моста. Полагаем w2= lim w (t). и т. д. t ^Т 2 Полуинтервал [ts,ts+1). Пусть x* - измеренное первым игроком в момент времени τs положение фазового вектора. В общем случае ws ^ x*. Управление us = const первого игрока на полуинтервале [ts,ts+1) определяем из условия (zs,Bus\ = min(z ,Bu),, (2.4) s u e PX где zs = xs - ws. Если условие (2.4) определяет вектор us e P неоднозначно, то берется любой из них. Движение реального динамического объекта получим интегрированием дифференциального уравнения X = A (t) x + B (t)(us + v (•)), x(Т ) = Xs , te[Ts, Ts+1 ). Полагаем xs+1= lim x (t). Движение t ^t+1 "поводыря" w(•) отождествим с тем решением дифференциального уравнения в контин-генциях w e A (t) x + B (t)(P + vs), w (Ts ) = ws , t e[Ts ,Ts +1 ) , (zs,Bvs\ = max(z ,Bv), \ ' veQ ' ' для которого выполнено включение w(ts+1) e W (ts+1). Такое решение существует по определению стабильного моста. Полагаем ws+1= lim w (t). и т. д. t ^Ts+1 Таким образом, на каждом полуинтервале [ts,ts+1), s = 0,1,...,k -1 разбиения промежутка времени [t*, T] будет получено движение "поводыря" w (•) и движение реального динамического объекта x (•) .Справедливо следующее утверждение [1]. Позиционная процедура управления с "поводырем" позволяет по любому £ > 0 подобрать величины Z (£)> 0 и 5 (£ )> 0, для которых бы выполнялось xА (0) < £ , где xА(-)- ломаная Эйлера, выходящая из начального положения (10, x0 )e W и порожденная процедурой управления с "поводырем", если длина шага разбиения А меньше д (£ )> 0, а точность измерения фазового вектора не ниже Z (£) > 0. 3. Численный эксперимент В рассматриваемой дифференциальной игре стабильный мост первого игрока, обрывающийся в момент времени 5 e [0, T] в на- чале координат, имеет вид W = {(t,x)|£ (t,x)< 0, t e[0,5]}, где £ 0 (t, x ) = T = max{0, max ^x, s (t)} + J minBB (t) u, s (t)ddz + l,SueP T + j max BB (t ) v, s (t ) ^dz t - max meM (3,1) S(4)={l e R 2| ||l|| = 1}, s (t ) = ( X [ T, t]) ' l °, т e [t, T], l0 e S(4) - вектор, доставляющий максимум в (3.1). При проведении численного эксперимента были установлены следующие значения параметров задачи. Каждое звено двух- звенного манипулятора имеет длину l1 = 12 = 1 м, масса схвата m=1 кг , массы стержней - m1 = m2 = 1 кг . Отклонение схвата манипулятора от начального положения определяется вектором x 0* 1-0.21 рад ^ 0.40 рад 0 рад сек рад V 0 ~к / и составляет величину р0 = 0.45177 . Заметим, что (0, x°*)e W . Принимается также, что а = 10 н • м, в = 1 н • м, д = 0.005 м . Все вычисления проводились в среде пакета Mathematica 8. В рамках численного эксперимента рассмотрены два случая. В первом случае в условиях неточного измерения фазового вектора игрок-союзник реализует свою стратегию в виде стандартного прицеливания на мост, а во втором случае – в форме процедуры управления с "поводырем". В процессе прицеливания на мост определение w0— точки моста, ближайшей к точке x £ W (t) = {x е R41 (t, x) e W}, t e [0,5] осуществляется путем решения задачи математического программирования на условный минимум с ограничением типа неравенства ( pl - x1 ) +( p2 - x2 ) +( p3 - x3 ) + +( P 4 - x4) ^ min, (3.2) s(t,x1,x2,x3,x4,)< 0. (3.3) Заметим, что задача (3.2), (3.3) является невырожденной задачей выпуклого программирования. Тогда необходимые условия локального минимума в форме правила множителей Лагранжа служат для нее и достаточными условиями глобального минимума. При реализации процедуры управления с "поводырем", описанной в предыдущем пункте, удержание "поводыря" на стабильном мосту на каждом шаге процесса осуществляется выбором управляющего па- раметра первого игрока из условия ds < 0. dt Случай первый. Управление манипулятором производится в форме стандартного прицеливания на стабильный мост в условиях неточного измерения фазового вектора. На рис. 3 показана траектория фазового вектора игры в проекции на первые две координаты, в предположении, что второй игрок действует самым неблагоприятным для первого игрока образом. Расстояние фазового вектора до начала координат (по всем четырем координатам) в конечный момент времени равно pk = 0.06224, что говорит о неэффективности приведенной процедуры управления. Рис. 3. Траектория движения управляемого объекта Случай второй. В условиях неточного измерения фазового вектора управление манипулятором осуществляется в форме позиционной процедуры управления с "поводырем". На рис. 4 показана траектория фазового вектора игры в проекции на первые две координаты, в предположении, что второй игрок действует самым неблагоприятным для первого игрока образом. Расстояние фазового вектора до начала координат (по всем четырем координатам) равно pk = 0.00031. В случае, когда второй игрок действует случайно, оно практически равно нулю. Полученные результаты являются приемлемыми. Рис. 4. График движения управляемого объекта при оптимальном действии помехи Заключение В работе численно подтверждено, что процедура управления с поводырем является эффективным способом управления в дифференциальной игре наведения в условиях неточного измерения фазового вектора игры. Этот факт позволил решить задачу возвращения схвата манипулятора на базовую траекторию с заданной степенью точности, в предположении, что его отклонение от базового закона движения в каждый момент времени измеряется с погрешностью.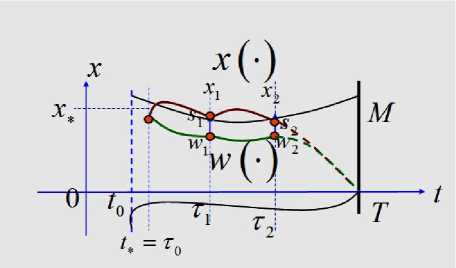
Список литературы Управление с "поводырем" двухзвенным манипулятором с вращательными парами
- Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1973. 456 с.
- Лутманов С.В., Попова Е.С. Игровые задачи управления двухзвенным манипулятором с вращательными парами//Проблемы механики и управления: межвуз. сб. науч. тр. Пермь, 2012. Вып. 44. С. 59-73.
- Лутманов С.В., Попова Е.С. Реализация процедуры управления с "поводырем" в одной антагонистической дифференциальной игре двух лиц наведения на целевое множество//Проблемы механики и управления: межвуз. сб. науч. тр. Пермь, 2013. Вып. 45. С. 39-54.


