Уравнение Орнштейна - Цернике в физике стеклообразного состояния

Под стеклом обычно понимают любой материал неорганического или органического происхождения, у которого отсутствует дальний порядок в структуре и вязкость которого выше 10 1 -10 14 Пуаз . Согласно молекулярно-кинетическим представлениям [1-3], в принципе все вещества могут быть получены в стеклообразном состоянии, если этому переходу не помешает кристаллизация. Можно осуществить переохлаждение и переход в стекло даже расплавов металлов и получить так называемые металлические стекла [3]. Поэтому, стеклообразное состояние часто определяют как неравновесное метастабильное состояние жидкости с замороженной структурой [4; 5].

Теплофизические и другие свойства стеклообразных твердых тел во многом определяются структурой жидкости, которая фиксируется в области стеклования. Вместе с тем в настоящее время нет общепризнанной теории перехода жидкость - стекло, а также нет полной ясности в природе жидкого и стеклообразного состояний вещества. Построение строгой статистической теории встречает большие трудности. Успехи, достигнутые в последнее время, касаются лишь равновесных свойств простых жидкостей со сферически симметричным парным потенциалом взаимодействия.

При исследовании методами статистической физики однородных и изотропных жидкостей в равновесном состоянии классикой стало использование уравнение Орнштейна — Цернике (ОЦ) [6-8]. Как показано в [7; 8], это уравнение является прямым следствием распределения Гиббса, если учитывать только парные взаимодействия частиц. В системе частиц с вышеуказанными свойствами уравнение ОЦ отражает пространственные корреляции между положениями любых трех частиц во всем объеме системы:

h ( r 12 ) = C ( r 12 ) + n J C ( r 13 ) h ( r 32 WV ⁽¹⁾

Здесь r ₁₂ = | r - r₂ |, r ₁₃ =| r - r₃ |, r ₃₂ = | r - r ₂1 — модули приращений радиус-векторов трех произвольно взятых частиц системы, коррелирующих между собой; h ( r ₁₂) — полная и C ( r ₁₂) — прямая корреляционные функции; n — концентрация частиц; интегрирование ведется по координатам третьей частицы по всему объему системы.

1 Применение уравнения Орнштейна — Цернике к стеклообразному состоянию

Использование уравнения ОЦ к описанию метастабильных состояний, к которым можно отнести стеклообразное состояние, является проблематичным [7; 8]. Однако, стеклообразное состояние в отличие от метаста-бильных жидкостей характеризуется большими временами релаксации частиц системы к структуре равновесных состояний, что позволяет применять уравнение ОЦ к стеклам, как к жидкостям с практически замороженной структурой.

В работе Малиевского с соавторами [9] было показано, что расщепление второго максимума радиальной функции распределения на два пика в системе твердых сфер, полученные с помощью уравнения ОЦ при плотностях твердого состояния, можно считать признаком аморфного состояния. Это предположение было подтверждено экспериментами по нейтронному и рентгеновскому рассеянию, и расщепление второго максимума корреляционной функции считается признаком аморфного состояния [10; 11]. Кроме этого, моделирование методом молекулярной динамики аморфного состояния в системе Леннарда — Джонса [12] также показы - вают такое расщепление.

Функцию h ( r ) в уравнении Орнштейна — Цернике (1) можно выразить через потенциал взаимодействия ф ( r ) и через бридж-функционал B [ h ( r )]:

h (r)

, - kT ) + y ( r ) + b : h ( r ) i

- 1,

где k — постоянная Больцмана, у ( r ) — непрямая корреляционная функция, равная разности между полной h ( r ) и прямой C ( r ) — корреляционными функциями: h ( r ) - C ( r ).

Ввиду невозможности использования в (2) бридж-функционала B[h(r)] в виде бесконечного ряда диаграмм, при решении уравнения ОЦ исполь- зуются процедуры замыкания, устанавливающие связь между полной и прямой корреляционными функциями. В нашем случае используется за- мыкание Мартынова — Саркисова [8], как наиболее подходящее для описания стеклообразного состояния:

B [ h (r)] ^ B (h (r)) = -1 - Y (r) +

nK(r)         Г

2 ( ) + 1 - 2 Y (r) kT \         ’

—

n^F 2 ( ^r ) " kT ,

где F 2 ( r ) — часть потенциала парного взаимодействия частиц ф ( r ), отвечающая за силы притяжения между ними. В наших расчетах используется известный потенциал Леннарда — Джонса:

ф( r) = 4s

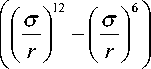
Здесь е — минимум потенциала, а — эффективный диаметр частиц.

Численное решение уравнения Орнштейна — Цернике (1) с использованием вышеуказанных выражений [13-16], позволяет найти двухчастичную или радиальную функцию распределения частиц g2(r12) = 1+ h(r12). Эта функция для однородных и изотропных систем зависит только от модуля разности радиус-векторов двух частиц r12 =| r - r, |. Она определяет расстояние между двумя частицами в радиальном направлении. Функция радиального распределения g2(r12) для однородной и изотропной жидкости, приведена на кривой 1 рисунка 1. Она отражает ближний порядок частиц в жидкостях — высокий и узкий первый пик, отражающий взаимное упорядоченное расположение частиц первой координационной сферы диаметром о = 1, затем быстрое убывание и расплывание по ширине следующих пиков, свидетельствующие о быстром исчезновении ближнего порядка.

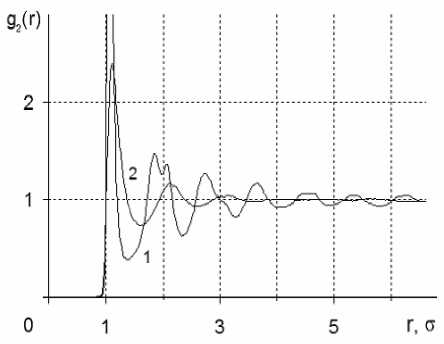
Рис. 1. Радиальная функция распределения g₂ (r) ЛД-системы.

1 — аморфное твердое тело, T * =0.25, n * =1.1;

2 — жидкость T * =1.0, n *=0.7; n * = n о ³ , T*=T/e ; получено методом молекулярной динамики.

Уменьшение температуры жидкости с достаточной скоростью вблизи точки фазового перехода жидкость — кристалл приводит к тому, что при резком уменьшении межчастичного расстояния, частицы жидкости не успевают перестроиться в упорядоченную кристаллическую структуру и образуют неравновесное стеклообразное твердое тела с замороженной структурой ближнего порядка жидкости. Такой переход не относится к фазовым переходам и является кинетическим явлением с большим временем релаксации, зависящим от скорости охлаждения, от сложности структуры и сил межчастичного взаимодействия, определяющих вязкость и другие структурно чувствительные свойства системы частиц.

Переход в стеклообразное состояние отражается на виде радиальной функции распределения в виде расщепления второго максимума на два пика на кривой 1 рисунка 1 [7; 17].

Плотность стеклообразного состояния выше плотности жидкого расплава, что приводит к уменьшению простора для передвижения частиц и неоднородности, носящей микроскопический характер. Поэтому, для применения уравнения Орнштейна — Цернике (1) к стеклообразному состоянию, предлагается ввести в это уравнение функцию распределения J ( r ₃), учитывающую микроскопическую неоднородность системы и зави-сящей только от расстояния между частицами:

^h ( r 12 ) = ^C ( r 12 ) + n J ^J ( r 3 ) ^C ( r 13 ) ^h ( r 32 ) d^V 3 .            ⁽⁵⁾

В стеклообразном состоянии подвижность частиц системы ограничена ближним окружением в пределах сферы с эффективным диаметром о :

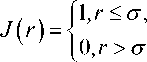
Подставляя (6) в выражение (5), получим замкнутое уравнения Орнштейна — Цернике пригодное для стеклообразного состояния:

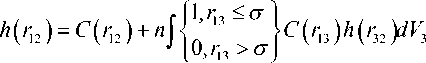
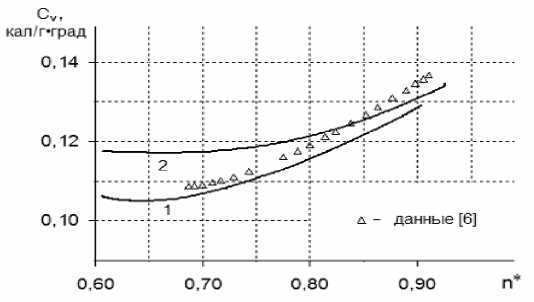
Рис. 2. Изохорическая теплоемкость аргона. T =120K, 1 — уравнение (1), 2 — уравнение (7).

С использованием алгоритма Малика — Лабиевского были рассчитаны радиальные функции распределения g₂ ( r ₁₂) = 1 + h ( r ₁₂) для систем частиц аргона в стеклообразном состоянии при решении выражения (7).

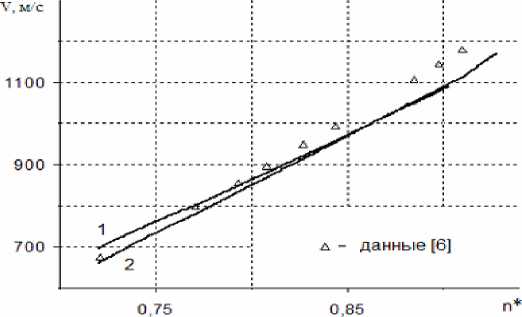
Рис. 3. Скорость звука в аргоне. T =120K.

1 — уравнение (1), 2 — уравнение (7).

Радиальная функция распределения позволяет рассчитать многие термодинамические свойства изучаемых систем, например теплоемкость, скорость звука и др.

На рисунках 2 и 3 приведены результаты расчетов теплоемкости и скорости звука в аргоне, показывающие, что модифицированное уравнение Орнштейна — Цернике (7) более пригодно при высоких плотностях.

Вышеприведенные результаты показывают, что модификация уравнения Орнштейна — Цернике (1) путем ввода в него одночастичной функции распределения J ( r 3 ), учитывающей различия между структурами жидкости и стеклообразного твердого тела позволяет получить более точные значения термодинамических параметров простых систем в микроскопически неоднородных состояниях.

Другой подход модификации уравнения Орнштейна — Цернике для исследования стеклообразного состояния на основе модели хаотического фазового перехода рассматривается в работе [18]. Для этого в уравнении Орнштейна — Цернике учитываются уравнения для прямой корреляционной функции C ( r 12 ), позволяющие отличить жидкое состояние от стеклообразного.

Заключение

Отличие стеклообразного состояния от жидкого должно быть каким-то образом отражено в уравнении Орнштейна — Цернике. Одним из способов учесть микроскопическую неоднородность стеклообразных тел является модификация уравнения Орнштейна — Цернике путем ввода в уравнение одночастичной функции распределения, учитывающей различия между структурами жидкости и аморфного твердого тела.

Другой способ позволяющий отличить переохлажденную жидкость от стекла заключается в модификации метода частичных функций распределения, в частности, модификации выражения для прямой корреляционной функции C ( r 12 ) в уравнении Орнштейна — Цернике.

Полученные интегральные уравнения физики для стеклообразных состояний являются приближенными и свидетельствуют о возможности описания аморфных состояний простых молекулярных систем с помощью модифицированного тем или иным способом уравнения Орнштейна — Цернике.