Уравнения соболевского типа с неизвестной правой частью

Настоящая работа посвящена исследованию разрешимости линейных обратных задач для дифференциальных уравнений

Au t + Bu = F (x,t), ( * )

Au tt + Bu = F (x,t) ( ** )

с операторами A и B , действующими по пространственным переменным (точный вид этих операторов будет приведен ниже).

Дифференциальные уравнения ( ∗ ) и ( ∗∗ ) в последнее время называют уравнениями соболевского типа [1–3], или же уравнениями составного типа [4], или же уравнениями, не разрешенными относительно производной [5].

Разрешимость краевых и начально-краевых задач для уравнений ( ∗ ) и ( ∗∗ ) представляется хорошо изученной — помимо названных выше монографий [1–5], можно назвать монографии [6–8]; что же касается журнальных статей, то их так много,что перечислить даже малую их часть весьма затруднительно.

В настоящей работе изучается разрешимость некоторых линейных обратных задач для уравнений ( ∗ ) и ( ∗∗ ). Близкие задачи достаточно хорошо изучены для классических дифференциальных уравнений второго порядка — см. монографии [9–14], и в значительно меньшей степени — для уравнений соболевского типа, уравнений составного типа и других неклассических дифференциальных уравнений.

Особенностью изучаемых в работе задач является то, что в них неизвестная правая часть определяется некоторой функцией, зависящей лишь от пространственных переменных. Для уравнений ( ∗ ) и ( ∗∗ ) в ряде работ [15–20] изучалась разрешимость линейных и нелинейных обратных задач в случае, когда неизвестный коэффициент (неизвестные коэффициенты) зависел (зависели) лишь от временной переменной. Что же касается случая, когда неизвестный коэффициент является функцией от пространственных переменных, то здесь можно назвать лишь работы [21; 22], в которых изучались линейные обратные задачи пространственного типа для некоторых частных случаев уравнения ( ∗∗ ).

Одним из методов исследования линейных обратных задач является метод, основанный на переходе от исходной задачи к новой задаче для уравнения более высокого порядка, не содержащего неизвестных коэффициентов — см. [23–26]. Именно этот метод будет применяться в настоящей работе, и именно он позволит получить существенно новые результаты для уравнений ( ∗ ) и ( ∗∗ ) с правой частью, содержащей неизвестный множитель, зависящий лишь от пространственных переменных.

Все построения и рассуждения в работе будут проводиться на основе пространств Лебега L _p и Соболева W _p ^l . Необходимые определения и описание свойств функций из этих пространств можно найти в монографиях [27–29].

Уточним, что целью настоящей работы будет доказательство существования и единственности регулярных решений для поставленных задач.

В работе будут изучаться дифференциальные уравнения ( * ) и ( ** ) модельного вида. Некоторые обобщения и усиления полученных результатов будут представлены в конце работы.

1    Постановка задачи

Пусть Q есть ограниченная область пространства R n с гладкой (бесконечно-дифференцируемой) границей Г, Q есть цилиндр Q х (0, T), 0 <  T <  + то , S = Г х (0, T) есть боковая граница Q. Далее, пусть b ij (x), i,j = 1,..,n, b o (x),h(x,t) и f(x,t) есть заданные функции, определенные при x G Q, t G [0, T], △ есть оператор Лапласа, действующий по переменным x 1 , x 2 , .., x n , B есть дифференциальный оператор, действие которого по заданной функции v(x) определяется равенством

∂

Bv =     (b j (x)v x j ) + b o (x)v,

∂x i

(здесь и далее по повторяющимся индексам ведется суммирование в пределах от 1 до n).

Обратная задача I: найти функции u(x,t) и q(x), связанные в цилиндре Q уравнением

4ut + Bu = f (x,t) + q(x)h(x,t),(1)

при выполнении для функции u ( x, t ) условий

u(x,t)|s = 0,(2)

u(x, 0) = 0,     x G Q,(3)

u(x,T) = 0, x G Q.(4)

Обратная задача II: найти функции u(x, t), q(x), связанные в цилиндре Q уравнением

4utt + Bu = f (x,t) + q(x)h(x,t),(5)

при выполнении для функции u(x,t) условий (2)-(4), а также условия ut(x, 0) = 0,     x G Q.(6)

В обратной задаче I условия (2) и (3) есть условия начально-краевой задачи для уравнения (1), называемого в некоторых источниках псевдо-параболическим [1], условие же (4) есть условие переопределения, необходимость которого диктуется наличием дополнительной неизвестной функции q(x).

В обратной задаче II условия (2), (3) и (6) можно трактовать как условия первой начально-краевой задачи для нестационарного уравнения (5), условие же (4) можно трактовать как условия переопределения. Можно и по иному трактовать условия обратной задачи II.

2    Разрешимость обратных задач I и II

Всюду ниже будем считать выполненным условие

h(x,t) >  h ₀ > 0    при    (x,t) € Q.                (7)

Определим функции h 1 (x, t), h ₂ (x, t) и F(x,t,£,n) при (x,t) € Q, £ = (£ i ,..,£ n ) € R ⁿ , n € R:

h t ^(x,t)

h ^{1 (X,t)}       h(x,t) ,

• h ₂ (x,t) = h i (x,t)b o (x) + ^(b ij (x)h i x i (x,t)V ,

F (x, t, _{, n) = XX 6 2 - ( X h l X i (x, % ) n + h 2 (x, t)n ² .

i =0         i =0

Далее определим операторы C 1 и C 2 :

C 1 = h i (x,t)A + B,

C 2 = - (h i (x,t)B - h i t (x,t)A).

Теорема 1. Пусть выполняются условие (7), а также условия bij (x) € C 3(fi),   bij (x) = bj4x),_ i,j = 1,..,n, bij (x)£i£j > 0 при x € Q ,£ € Rn;

b ₀ (x) € C (Q), b ₀ (x) <  0 при x € Q;                (9)

h(x,t) € C 3 (Q), h 1 (x,t) <  0, h _{1 t} (x,t) <  0, h ₂ (x,t) >  0 при (x,t) € Q;

n

F(x,t,£,n) >  Y 0 X € 2 ,  Y 0 > 0,  (^x,t) ^{G Q} ,  £ 6 R n ,  n ^G R;    ⁽¹¹⁾

i =0

оператор C i эллиптичен при (x, t) G Q, оператор C ^ эллиптико-параболичен в Q.

Тогда для любой функции f (x, t) такой, что f (x,t) G L ₂ (Q), f t (x,t) G L 2 (Q), обратная задача I имеет решение { u(x,t), q(x) } , для которого выполняются включения

• ^d k d_tX ^{,t )} G L ₂ (0,T; W 2 №), k = 0,1, 2, q(x) G L ₂ (Q).

Доказательство . Определим функцию f i (x,t):

^f i ^(x,t) = h^(x,t) ffTxT)) .

h(x, t) _t

Рассмотрим краевую задачу: найти функцию u(x,t), являющуюся в цилиндре Q решением уравнения

4 u tt + C i u t + h i Bu = f i (x, t)

и такую, что для нее выполняются условия (2)—(4).

Покажем, используя метод продолжения по параметру [30, гл. III, § 14], что данная задача имеет решение u(x,t) такое, что u(x,t), u t (x,t), u _tt (x,t) принадлежат пространству L 2 (0,T; W ^ (Q)).

Пусть А есть число из отрезка [0,1]. Рассмотрим семейство задач: найти функцию u(x,t), являющуюся в цилиндре Q решением уравнения

4 u tt + А [C i u t + h i Bu] = f i (x, t)

(13a)

и такую, что для нее выполняются условия (2)—(4).

Как следует из теоремы о методе продолжения по параметру, эта задача будет иметь решение из указанного класса для всех чисел λ из отрезка [0,1], если 1) задача (13o), (2)—(4) имеет решение, принадлежащее требуемому классу; 2) для всевозможных решений u(x, t) краевой задачи (13a), (2)—(4) при выполнении условий теоремы имеет место априорная оценка kukL2(0,T;W22(Q)) + kutkL2(0,T;W22(Q)) + kuttkL2 (0,T;W22(Q)) — R0kfikL2(Q)

с постоянной R o , определяющийся лишь функциями b ij (x), i,j = 1,..,n, b o (x), h(x,t), областью Q и числом T .

Выполнение пункта 1) очевидно. Покажем, что для всевозможных решений u(x,t) краевой задачи (13 д ), (2)—(4) действительно имеет место требуемая оценка.

Умножим уравнение (13 д ) на функцию u(x,t) и проинтегрируем полученное равенство по цилиндру Q. После несложных преобразований с использованием условий (8)—(11) придем к оценке

^X    u ² _{x i t} dxdt ≤ R 1    f ₁ ² dxdt

i=1 Q               Q с постоянной R1, определяющейся лишь функциями bij(x), i,j = 1,..,n, bo(x) и h(x, t).

На следующем шаге умножим уравнение (13д) на функцию —Ciu(x, t) и проинтегрируем по цилиндру Q. Полученное равенство нетрудно преобразовать к виду j AutC1utdxdt —

Q

2 У h i tt (Au) ² dxdt +

Q

C 1 uC 2 udxdt =

Q

f 1 C 1 udxdt.

Q

Поскольку оператор C1 эллиптичен в Q, то первое слагаемое левой части (16) можно преобразовать, используя технику доказательства второго основного неравенства для эллиптических операторов [28]; учитывая дополнительную оценку (15), придем к неравенству f AutC1utdxdt > R2 X у uXixjtdxdt — R3,

Q                        i,j=1 Q постоянные R2 и R3 в котором положительны и определяются лишь функциями bij(x), i,j = 1,..,n, bo(x) и h(x,t), а также областью Q и числом T .

Преобразуем аналогичным образом третье слагаемое левой части (16), учитывая, что оператор C 2 эллиптично-параболичен в Q, применяя теоремы вложения и оценку (15) получим, что справедливо неравенство

C 1 uC 2 udxdt ≥ I -

Q

n

δXZ

i,j =1 _Q

u X-x j t dxdt — M (d),

в котором I есть некоторый неотрицательный интеграл, δ есть произвольное положительное число, число же M (d), помимо числа d, определяется также функциями b ij (x), i, j = 1, ..,n и b o (x), а также областью Q и числом T .

Неравенства (17) и (18) вместе с выбором числа δ малым означают, что следствием равенства (16) будет вторая априорная оценка решений u(x,t) краевой задачи (13 д ), (2)—(4):

X I u X i x j t dxdt <  R 4 j fdxdt;

i,j=1Q                   Q постоянная R4 здесь вновь определяется лишь функциями bi (x), i, j =

1, ..,n и b o (x), а также областью Q и числом T .

Из оценок (15) и (19) вытекает очевидная третья оценка решений u(x,t) краевой задачи (13 д ), (2)-(4):

X j u X i x j _tt dxdt <  R 5 j fdxdt;

i,j=1Q                    Q постоянная R5, как и постоянные R1—R4, определяется функциями bij (x), i, j = 1, ..,n и bo(x), а также областью Q.

Оценки (15), (19) и (20) и дают в целом требуемую оценку (14). Как уже говорилось выше, из этой оценки следует, что краевая задача (13 д ), (2)–(4) будет разрешима в требуемом классе для всех чисел λ из отрезка [0,1]. Но тогда и задача (13), (2)-(4) будет иметь решение u(x,t), также принадлежащее требуемому классу.

Уравнение (13) можно записать в виде

( h ^(Au t + ^{Bu) —} Т^ = 0.

∂t h              h

Интегрируя, получим равенство

Au t (x, t) + Bu(x, t) = f (x, t) + h(x, t)q(x),               (21)

в котором q(x) есть функция

q^(x) = ^7¹nт^[Au t ^{(x, 0) - f(x},^0)]. h ( x, 0)

Принадлежность функции q(x) пространству L 2 (Q) очевидна. Уравнение (21) и означает, что функции u ( x, t ) и q ( x ) представляют собой искомое решение обратной задачи I.

Теорема доказана.

Исследование разрешимости обратной задачи II будет проведено в целом по той же схеме, по какой было проведено исследование разрешимости обратной задачи I.

Пусть для коэффициентов bij(x), i,j = 1,..,n, bo(x) оператора B выполняются условия гладкости теоремы 1, и пусть β0 есть фиксированное число, v(x) есть функция из пространства W2(Q) nW2(Q)- Используя простейшие алгебраические неравенства, а также применяя второе основное неравенство для эллиптических операторов, нетрудно показать, что для функции v(x) имеет место оценка kBv — e04vkL2(Q) < eik4vkL2(Q) + e2kvkWl(Q),          (22)

в которой числа в 1 и в 2 определяются функциями b ij (x), i,j = 1, ..,n и b o (x), а также числом в о и областью Q.

Оценка (22) нам понадобится для доказательства разрешимости обратной задачи II.

В дальнейшем будем считать, что функция h зависит лишь от переменной t; общий случай h = h(x, t) будет отличаться от рассмотренного большей громоздкостью условий и выкладок.

Через v = (v i ,.., v n ) будем обозначать вектор внутренней нормали к Г в текущей точке.

Теорема 2. Пусть выполняются условие (7), а также условия bj(x) G C 1(Q),   bij(x) = bji(x),   i,j = 1,..,n, bij(x^iCj > 0 при x G Q,^ G Rn;

b ₀ (x) G C (Q), b ₀ (x) <  0 при x G Q;              (24)

h = h(t) G C 3 ([0,T]),   (T - t)h i (t) <- 2 ,

((T - t)h i (t)) tt <  0 при t G [0,T];

а также одно из условий bij (x)vivj = 0 при x G Г или для оператора B существует число во из промежутка (-то; 0] такое, что для числа β1, определенного в (22), выполняется неравенство

- ^{+ (}Т — t^)h i ^(t)— > 0.                     ⁽²⁷⁾

2                  П

Тогда для любой функции f (x,t) такой, что f (x,t) G L2(Q) , ft(x, t) G L2(Q) обратная задача II имеет решение {u(x,t), q(x)} такое, что dku^t) G L2(0,T; W22(Q)), k = 0,1, 2, 3, q(x) G L2(Q).

Доказательство . Рассмотрим краевую задачу: найти функцию u(x, t), являющуюся в цилиндре Q решением уравнения

4 u ttt + h i 4 u tt + Bu t + h i Bu = f i (x, t)

и такую, что для нее выполняются условия (2)–(4) и (6). Разрешимость этой задачи вновь будет установлена с помощью метода продолжения по параметру.

Для чисел А из отрезка [0,1] рассмотрим семейство краевых задач: найти функцию u(x,t), являющуюся в цилиндре Q решением уравнения

4 u ttt + А [h i 4 u tt + Bu t + h i Bu] = f i (x, t)            (28 д )

и такую, что для нее выполняются условия (2)-(4) и (6). При А = 0 эта задача имеет решение u(x, t) такое, что u(x, t) и все ее производные по переменной t до третьего порядка включительно существуют и принадлежат пространству L 2 (0, T ; W ^ (О)). Покажем, что для произвольных регулярных решений задачи (28 д ), (2)-(4), (6) имеют место необходимые априорные оценки.

Умножим уравнение (28 д ) на функцию (T — t)u(x, t) и проинтегрируем по цилиндру Q . После несложных преобразований получим равенство

PP J [3 + А(Т — t)] u^.tdxdt — А J [ 1 + (T — t)hi(t)] bijuxiuxjdxdt— i=1 Q                            Q

2 E ^J [(T — t)h i (t)] tt u X i dxdt + А ^{J [} 1 + (T — t)h i (t)^] b o u²dxdt = i =1 Q                             Q

J (T — t)f 1 udxdt.

Q

Используя условия (23)–(25) и применяя неравенство Юнга, нетрудно получить первую априорную оценку решений u(x, t) краевой задачи (28), (2)–(4), (6):

X / u X i t dxdt <  N 1 У f 2 dxdt

i=1 Q               Q с постоянной Ni, определяющейся лишь функцией h(t) и числом T.

На следующем шаге умножим уравнение (28 д ) на функцию — (T — t) 4 u(x,t) и проинтегрируем по цилиндру Q. Получим равенство

PP / [2 + (T — t)hi(t)] (4ut)2dxdt— i=1Q

2 J [(T — t)h 1 (t)] _tt ( 4 u)²dxdt — J(T — t)Bu _t 4 udxdt —       (30)

QQ

J (T — t)h 1 (t)Bu 4 udxdt = — J (T — t)f 1 4 udxdt.

Пусть выполняется условие (26). Тогда третье слагаемое I 3 левой части (30) преобразуется к виду

-

I 3 =

2 j b ^ij u x i x k u x j x k dxdt Q

(появляющиеся при интегрировании по частям граничные интегралы будут равны нулю вследствие условия характеристического вырождения (26) и условий (3) и (4)), и тем самым будет представлять собой неотрицательную величину. Далее, четвертое слагаемое левой части (30) преобразуется к сумме неотрицательной величины и величины, являющейся ограниченной вследствие оценки (29). Учитывая далее условия теоремы и пременяя неравенство Юнга, получим, что при выполнении условия (26) из равенства (30) вытекает оценка

j ( 4 u t ) 2 dxdt <  N2

Q

f ₁ ² dxdt,

Q

постоянная N в которой определяется функциями b ^ij (x), i,j = 1,..,n, b o (x) и h(t), а также областью Q и числом T .

Пусть теперь выполняется условие (27). Для интеграла I 3 выполняется равенство

I 3 =

— ^в0 /( 4 u)²dxdt Q

j (T — t)(Bu t — e o 4 u t ) 4 udxdt.

Q

Первое слагаемое правой части данного равенства неотрицательно, второе же нетрудно оценить с помощью неравенства Гельдера, неравенства

TT

/ v 2 (t)dt <  ( ^T )  /

π

v _t ² ( t ) dt,

справедливого для любой функции v(t) из пространства W ^ ([0, T ]), а также неравенства (22) и оценки (29):

j(T — t)(Bu t — e o 4 u t ) 4 udxdt <

Q

^ ^в1 I ( 4 u t ) 2 dxdt+N ₃ Q

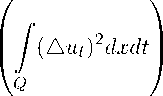
(число N 3 здесь определяется лишь числом N i , областью Q и числом T ).

Проведенные выше рассуждения и выкладки, а также условие (27) означают, что следствием равенства (30) будет оценка

I ( 4 u t ) ² dxdt <  N

Q

I f l dxdt

Q

с постоянной N, определяющейся функциями b ij (x), i, j = 1, ..,n, b o (x) и h(t), а также областью Q и числом T .

Последняя оценка j ^dxdt < N4

Q

У f l dxdt

Q

очевидным образом вытекает из оценок (29), (31) и (32), а также из неравенства

j ( 4 u tt ) ² dxdt <  5

Q

j (bumfdxdt +

Q

C (5) j

( 4 u _t ) ² dxdt,

Q

в котором δ есть произвольное положительное число (см. [31]).

Оценки (29), (31) и (32), а также (33) дают окончательную оценку