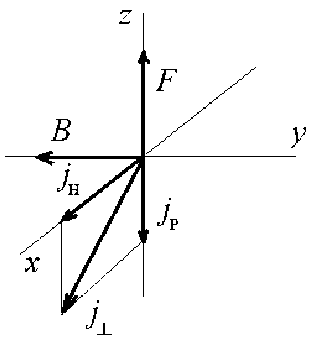Ускорение заряженной частицы под влиянием соударений в поле электромагнитной волны

Заряженная частица в поле электромагнитной волны колеблется и, вообще говоря, испытывает систематическое ускорение под действием усредненных по периоду колебаний пондеромоторных сил. Известны силы Миллера и Абрагама, пропорциональные величинам V E ² и d E ²/ д t соответственно. Здесь Е – амплитуда колебаний электрического поля волны. Если движение происходит в постоянном неоднородном магнитном поле В , то при исследовании ускорения следует учитывать также силу Питаевского, пропорциональную E ²V_H B , где V_H =B^-1 B ^ V (см., например, [Морозов, Соловьев, 1963]). Все эти силы играют большую роль в физике бесстолкновительной космической плазмы (см. [Zotov, Guglielmi, 2010] и указанную там литературу). В данной статье мы покажем, что при наличии столкновений возникает еще одна сила, пропорциональная v E ², где v - частота столкновений.

Сделаем ряд предварительных пояснений, следуя обзору [Болотовский, Серов, 2003]. Рассмотрим плоскую монохроматическую волну в вакууме. Пусть магнитное поле В отсутствует. Понятно, что в этом случае силы Абрагама, Миллера и Питаевского не возникают. При указанных условиях задача о поведении заряженной частицы в волне имеет аналитическое решение, найденное Волковым в 1935 г. Частица совершает финитное движение, описывая в пространстве плоскую замкнутую кривую [Ландау, Лифшиц, 1973]. Болотовский и Серов обратили внимание на важность того обстоятельства, что найденное решение является частным [Болотовский, Серов, 2003]. Оно справедливо в движущейся равномерно и прямолинейно сопутствующей системе отсчета, в которой частица покоится в среднем по периоду колебаний поля. В то же время интерес может представлять поведение частицы в лабораторной системе отсчета. В этом случае движение частицы существенным образом зависит от начальных условий. Оказывается, что частица не только колеблется, но и систематически дрейфует в направлении распространения волны (эффект Болотовского–Серова). Скорость дрейфа равна

V D = e ² E ² ( cos2 ^ + 2 ) /(4 m ² to ² c ). (1)

Здесь е и m – заряд и масса частицы, ω и φ – частота и фаза волны, c – скорость света.

Ускорение частицы вследствие соударений

Мы используем следующую эвристическую модель. Допустим, пробная заряженная частица, движущаяся в поле волны, испытывает случайные столкновения с другими частицами. (Ниже для простоты будем считать их неподвижными нейтральными частицами.) При каждом столкновении происходит «обновление» начальных условий и вследствие эффекта Болотовского–Серова пробная частица приобретает дополнительную скорость V D , поэтому ускоряется в направлении распространения волны под действием силы

F = v e ² E 2 /(2 mc to ²).                           (2)

При выводе (2) из (1) мы произвели усреднение по фазе φ.

Подтвердим справедливость (2) путем прямого расчета. Пусть плоская монохроматическая волна поляризована линейно и распространяется в направлении z . Ориентируем оси x , y так, чтобы неисчезающими были компоненты E x электрического и b y магнитного поля волны. Подсчитаем z- компоненту силы Лоренца ( e / c ) v × b и усредним ее по периоду колебаний:

F l = ( e /2 c ) Re ( v* _x b y ) .                             (3)

Здесь v – скорость колебаний частицы, b – магнитное поле волны, звездочка означает комплексное сопряжение. Чтобы найти vx , воспользуемся линеаризованным уравнением движения dv, / dt = ( e / m) E,-v,.(4)

xxx

Второй член в правой части моделирует столкновения. Решая (4), находим vx = eEx (v + ito) /(mto2 )(5)

при условии, что ν²<<ω². Подставим (5) в (1) и учтем, что в вакууме b_y = E_x . Получим

FL =v e 2 E 2/(2 mc to2).(6)

А . В . Гульельми , О . Д . Зотов , Б . И . Клайн

Результат расчета подтверждает формулу (2), найденную из эвристических соображений.

Влияние плазмы и магнитного поля

Сопоставим F с силой Миллера

F m =- ( e 2 /(4 m e w ²) ) V E ². (7)

Она возникает в том случае, когда волна распространяется не в вакууме, а в плазме. Пусть вначале внешнее магнитное поле B отсутствует. Если ω>>ω 0e , то показатель преломления не отличается от единицы и формула (6) не изменяется. Здесь ω 0e =(4π e ² N e / m e )^1/2 – частота Ленгмюра, N e – концентрация электронов. Из-за соударений амплитуда волны экспоненциально уменьшается в направлении распространения. При ν_e<<ω имеем

E ^ exp ( -к г ) , (8)

где x = v _e w 0e /(2 w ² c ) [Гинзбург, 1967]. Подставляя (8) в (7), находим, что F превышает F M в 2(ω/ω 0e )² раз. Разумеется, данный результат относится только к рассмотренной здесь модели при указанных выше условиях.

Чтобы избежать громоздких формул, возникающих при учете поля B, ограничимся рассмотрением нескольких частных случаев. Рассмотрим вначале высокочастотный предел, когда ω>>max(Ωe, ω0e, νe), где Ωe=eB/(mec) – циклотронная частота электронов. Если волна распространяется параллельно силовым линиям B, то под действием силы F электроны движутся в том же направлении и создают постоянный продольный ток j = eE2w2e/(8nme cw2), (9) текущий в направлении, противоположном направлению распространения волны. Если же волна распространяется перпендикулярно к силовым линиям, то возникает ток Холла jh = veE2

Теперь рассмотрим низкочастотный предел и определим его условием ω<<Ω_p, где Ω_p=eB/m_pc – циклотронная частота протонов. Дополнительно будем считать, что Ωp<<ω0p и νp<<ω. Здесь ω0p=(4πe²Np/mp)^1/2, причем Np=Ne (условие квазинейтральности плазмы). Как и выше, ограничимся случаями строго продольного и строго поперечного распространения волны.

Вдоль внешнего магнитного поля распространяются поперечные волны правой и левой круговой поляризации [Гинзбург, 1967]: E(t)=(1, ±i, 0)Eexp(ikz–iωt). Элементарный расчет показывает, что сила, действующая на протон, в низкочастотном пределе не зависит от поляризации, параллельна направлению распространения и равна

Возбуждение тока ji силой F, ортогональной магнитному полю B.

F = ( b / B )2 V_pmpca.                              (11)

Здесь b=(c/cA)E – магнитное поле волны, cA = B /^4nm_pN_p - скорость Альфвена. Сила, действующая на электрон, в ~ ^m_p / m_e раз меньше.

Сопоставим (11) с силой Абрагама, которая возникает при амплитудной модуляции волнового поля. Допустим, что амплитуда b(t) есть функция времени, мало меняющаяся за время ~1/ω. Тогда вместо (11) имеем

F = m_pcA (v_p+ d/dt)(b/B)2.                   (12)

Видно, что силой Абрагама (второй член в правой части) можно пренебречь, если частота соударений много больше характерных частот амплитудной модуляции.

Поперек внешнего магнитного поля на низких частотах распространяется быстрая магнитозвуковая волна с фазовой скоростью c_M= ^cA + cS, где c_S -скорость звука [Альфвен, Фельтхаммар, 1967]. Ориентируем координатные оси так, что B=(0, 1, 0)B. Тогда при распространении вдоль оси z волна поляризована следующим образом:

E(t) = (1, 0, 0) E exp (ikг - iwt),

b(t) = (0,1, 0) b exp (ikг - iwt).

Здесь b=(c/cM)E. Сила равна

F = ( b / B )2 Vpmpcm/2.                         (13)

Как и во всех предыдущих случаях, она параллельна направлению распространения. Под действием силы ион дрейфует поперек силовых линий внешнего магнитного поля со скоростью V=(c/eB²)F×B.

Обсуждение

Идея об ускорении заряженной частицы под влиянием соударений в поле бегущей электромагнитной волны может оказаться полезной при решении некоторых задач космической электродинамики. Например, одной из трудных задач является интерпретация эффектов воздействия индустриальной активности на режим низкочастотных колебаний магнитосферы [Guglielmi, Zotov, 2007; Zotov, Gug- lielmi, 2010]. При обсуждении соответствующих наблюдений предлагались различные механизмы демодуляции в ионосфере высокочастотных полей промышленного происхождения. Представление о возбуждении токов (9), (10) высокочастотной волной дает дополнительную возможность для поиска в этом направлении.

Рассмотрим еще несколько примеров. По наблюдениям на ИСЗ ISEE 2 и IMP8 обнаружено некоторое замедление солнечного ветра перед фронтом околоземной ударной волны – в так называемой области форшока [Bonifazi et al., 1980]. Известно, что в этой области существует перманентный поток низкочастотных (ω<<Ωp) волн правой круговой поляризации [Guglielmi, 1974]. Волны распространяются вдоль силовых линий межпланетного магнитного поля навстречу солнечному ветру. Поэтому естественно связать указанное замедление ветра с пондеромоторной силой (11). (Напомним, что направление силы F совпадает с направлением распространения волн.) Нетрудно увидеть, что максимальная величина замедления составляет δ Vmax=(b/B)²cA. Возьмем типичные значения b=3 нТл, B=7 нТл, c_A=50 км/с и получим δ V_max≈ 10 км/с при средней скорости ветра 500 км/с. Оценка δV_max не противоречит наблюдениям, но этим вопрос о происхождении эффекта замедления, разумеется, не решается. Во-первых, поток низкочастотных волн в области форшока неоднороден и нестационарен, так что необходимо еще учесть действие сил Миллера и Абра-гама на ионы солнечного ветра. Оценка замедления дана здесь лишь как иллюстрация возможного использования формулы (11) при анализе естественных физических процессов. Во-вторых, не вполне ясно, что надо понимать под частотой соударений в «бесстолкновительной» межпланетной плазме. Обычно в связи с этим говорят об аномальной или эффективной частоте соударений νef, величина которой определяется мелкомасштабной плазменной турбулентностью. Численные значения νef достоверно не известны. Теоретические оценки на этот счет неопределенны, а надежные экспериментальные оценки νef отсутствуют. (Подчеркнем, что речь идет об ионах. Для электронов эффективная частота соударений известна, в частности, по данным об аномальной электропроводности бесстолкновительной плазмы.) Величина δ V_max≈ 10 км/с, довольно близкая к измеренным значениям, получена нами в предположении, что время, за которое частица, двигаясь со скоростью солнечного ветра, переместится от передней границы форшока до фронта околоземной ударной волны, заметно превышает величину 1/νef. Это дает грубую оценку νef>10^–2 с^–1, если принять предложенную интерпретацию эффекта замедления.

В случае низкочастотной волны левой круговой поляризации, распространяющейся вдоль внешнего магнитного поля, специальный интерес представляет задача об ускорении тяжелого иона массой m_i>>m_p. (Тяжелыми являются, например, ионы O⁺ в водородной плазме, заполняющей магнитосферу Земли, металлические ионы в солнечной короне и т. п.)

Поскольку Ω_i<<Ω_p, то возможен циклотронный резонанс при условии ω=Ω_i, совместимом с условием ω<<Ωp. Вместо (11) получим

F = Vie²E2/(mica [(®-П_£)²+V²]), (14) откуда следует, что при резонансе сила F в (Ωi/νi)² раз больше, чем без него.

Случай поперечного распространения низкочастотных волн также представляет интерес для физики космической плазмы. По магнитопаузе, отделяющей магнитосферу Земли от горячей солнечной плазмы, распространяются поверхностные волны большой амплитуды. Преимущественное направление распространения ортогонально силовым линиям геомагнитного поля, примыкающим к магнитопаузе. Будем считать, как это обычно принято, что ионы солнечного ветра испытывают эффективные соударения, обусловленные мелкомасштабной турбулентностью. Если так, то существует сила параллельная магнитопаузе и перпендикулярная силовым линиям геомагнитного поля. Под действием этой силы ионы солнечного ветра могут перемещаться поперек силовых линий со скоростью ~сА(b/B)²(νef/Ωp) и проникать в магнитосферу на глубину порядка длины поверхностной волны при благоприятной ориентации направления распространения относительно направления геомагнитных силовых линий.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 0905-00048).