Условие стеклования в модели делокализованных атомов

Общая теория стеклования представляет собой на данный момент сложную и до сих пор нерешенную проблему теоретической физики. Подтверждением тому является многообразие феноменологических теорий и подходов, описывающих процесс стеклования, и которые в принципиальных вопросах отличаются коренным образом. В то же самое время микроскопические теории, обладая современными перспективными методами, не в состоянии дать количественную картину процесса стеклования сложных некристаллических систем.

С другой стороны, при качественном рассмотрении явлений перехода жидкость — стекло для различных неупорядоченных систем выявляются общие тенденции в виде универсальных правил и критериев.

В данной работе приведен краткий анализ наиболее популярных современных работ, касающихся критерия перехода расплава в твердое стеклообразное состояние. Предложено условие стеклования, следующее из модели делокализованных атомов, свободное от неточностей, присутствующих в ранее опубликованных работах других авторов в виде кон -стант, имеющих расплывчатый физический смысл.

• 1    Переход жидкость — стекло в релаксационной теории

В теории стеклования принципиально важное значение имеет момент перехода жидкости в твердое стеклообразное состояние. При температуре стеклования в зависимости от структуры стекол теряется подвижность кинетических единиц с характером взаимодействия частиц, свойственным данной структуре. Тем не менее, рассматривая стеклование жидкости как релаксационный процесс, можно заметить, что определяющее значение имеет функциональная связь времени релаксации структуры т со скоростью охлаждения расплава q [1-5].

Опубликованные критерии стеклования в разных источниках идентичны критерию Бартенева [1]:

q T g = C ,                               (1)

где q = | dT / dt | — скорость изменения температуры в ее абсолютном значении при нагревании или охлаждении системы, т_д — время релаксации при температуре стеклования T_g , C — эмпирическая константа.

Авторы [6] в результате решения предлагаемого ими уравнения указывают на критерий перехода жидкость — стекло уравнение стеклования:

q T g = 5 T g .                             (2)

Температура стеклования, по их мнению [ 13 ] , отвечает условию:

dT dT

T = T g

q

Сравнение уравнений (1) и (2) приводит к тому, что эмпирический параметр С в уравнении Бартенева обретает смысл полосы температур, в диапазоне которой при понижении температуры расплав переходит в стекло .

В исследовании других авторов [2; 7] считается, что жидкость перехо- дит в твердое состояние, при наступлении условия, при котором время структурной релаксации τ и характерное время изменения температуры τT будут иметь по порядку величины равные значения:

T T ddT V т ~ t _t = — = T I — I q V dt )

,

• т. е. вводится следующий кинетический критерий стеклования

  1 { dT )

  I к

  T ( dt )

  
  

  = C 3 ,

  
  

  C ₃ « 1 .

  
  
  
  

  T = T g

  
  

Если быть точным, постоянная C ₃ приравнена единице в виде постулата, без особого обоснования.

2 Условие стеклования в модели делокализованных атомов

В результате тепловых флуктуаций атомов неупорядоченной системы образуется объем, названный флуктуационным объемом:

A Ve = Ne Ave , где Ne — число делокализованных атомов (кинетических единиц), Jve — элементарный флуктуационный объем, требуемый для делокализации атома, т. е. его предельного смещения из локального равновесного положения. Доля флуктуационного объема fg, замороженная при температуре стеклования Tg есть один из параметров модели делокализованных атомов, и слабо зависит от природы аморфных веществ [8; 9] (таблица):

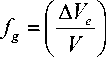
» 0.020 - 0.030.

T = T g

Тем более, для стекол одного класса эта величина оказывается практически универсальной постоянной .

Уравнение Вильямса — Ландела — Ферри (ВЛФ) [ 10 ] in кП =- C T - T g

к ( T g )      - T - T g + C 2

содержит константы, которым можно придать физический смысл исходя из модели делокализованных атомов [8]:

C 1         ,       C^          ,

1  fg         в где ef — коэффициент теплового расширения флуктуационного объема при температуре стеклования. Здесь следует подчеркнуть, что произведение коэффициента теплового расширения флуктуационного объема и температуры стеклования efTg = fg ln(1/ fg)

является только функцией доли флуктуационного объема f g , замороженной при температуре стеклования [ 8 ] .

Из уравнения ВЛФ (5) найдем время релаксации и решим совместно с выражением условия стеклования (3), результат чего запишем в следующем виде:

q ^ g

C

C 1 .

Анализ уравнений (6)-(8) приводит к уточненному уравнению стеклования Бартенева (1) в терминах модели делокализованных атомов:

f

^{q T g} = wT f ) ^Tg .

Разделив уравнение (9) на температуру стеклования, приходим к обобщенному кинетическому критерию стеклования:

q ^g- = —f^ ---= С = const » 7 - 10 ^{- 3}.

T g   ^1п(1/ f g )     g

Чтобы получить температуру Tg, это выражение надо записать в следую- щем виде:

i

T

dT dt

T

T = T g

= C g .

Таким образом, подвергнув критерий стеклования авторов работ [2; 7] обобщению и модификации, получили новое условие стеклования. Кроме того, у авторов [2; 7] постоянная С ₃ ~ 1, а здесь, в нашем новом критерии эта константа обретает физический смысл:

C 3 = C g

f g

1n(1/ f g )

~ const ~ 7 - 10 ³,

т. е. эта константа равна части флуктуационного объема, замороженной при температуре стеклования, с точностью до логарифма обратного значения этой величины, или, другими словами, процесс перехода жидкости в стекло становится возможным при замораживании некоторого определенного значения доли флуктуационного объема.

Расчеты значения константы стеклования C_g приведены в таблице. Замечаем, что постоянная С ₃ не может быть приблизительно равна единице. Действительно, для силикатных стекол при T_g ® 800K произведение скорости охлаждения на время релаксации при температуре стеклования, согласно вышеупомянутому критерию (4), как видим, имеет значение: qT_g ~ 800K [11]. Согласно результатам исследования [9] типичные значения этой величины для силикатных стекол находятся в пределах: q T _g « (5 * 10) K.

Расчеты произведения qτ g для силикатных и металлических стекол по предлагаемому условию стеклования (11) находятся в согласии с типичными данными для этого произведения и составляют ~ 4 - 6 K (Таблица).

Таблица

Параметры уравнения Вильямса — Ландела — Ферри C 1 , C 2

и константа условия стеклования C g некристаллических твердых тел

Вещество	т T g , K	C 1	C 2 , K	δ T = C 2 , g C 1 K	1 f g С 1	C g ⋅ 103	C g T g , K
1	2	3	4	5	6	7	8
Неорганические стекла Na 2 O-SiO 2
Na 2 O, mol.% 15	782	36	430	12	0.028	7.8	6.10
20	759	36	390	11	0.028	7.8	5.92
25	739	35	355	10	0.028	7.8	5.76
30	721	35	322	9	0.028	7.8	5.62
33	712	35	304	9	0.028	7.8	5.55
35	705	35	291	8	0.028	7.8	5.50
Металлические стекла
Pd 40 Ni 40 P 20	602	39	93	2.4	0.026	7.1	4.27
Pt 60 Ni 15 P 25	500	37	95	2.6	0.027	7.5	3.75
Pd 77.5 Cu 6 Si 16.5	653	38	100	2.6	0.026	7.1	4.64
Fe 80 P 13 C 7	736	38	120	3.2	0.026	7.1	5.23

Также, в отличие от подходов других авторов, в предлагаемом нами условии стеклования (10) появляются температура стеклования и универсальная безразмерная константа. Пусть q g = ( T g / τ g ) характерная скорость охлаждения стеклообразующей жидкости, а q / q g относительная скорость охлаждения:

^q = ^q = C ≈ const ≈ 7 ⋅ 10 ^{- 3}. (12) q g ( T g / τ g ) ^g

Тогда новое условие стеклования можно сформулировать так. Жидкость переходит в твердое стеклообразное состояние, когда относительная скорость охлаждения становится равной определенной константе C g в момент времени релаксации τ g равному C g , являющийся частью характерного времени изменения температуры τ _T = ( T_g / q ):

ττ g= g=C ≈ const ≈7 ⋅10-3. τT(Tg/q)    g

Заключение

Проведен краткий анализ кинетических критериев стеклования Бартенева (1) и других авторов [7]. Привлечение модели делокализованных атомов к анализу приводит к следующему физическому смыслу эмпирической константы критерия в статьях других авторов. Константа равна части флуктуационного объема замороженной при температуре стеклования с точностью до логарифма обратного значения этой величины, или, иначе жидкость переходит в стекло при замораживании некоторого зна- чения доли флуктуационного объема. Анализ и обобщение в терминах используемой модели позволило получить новое условие перехода жидкость — стекло, в котором в отличие от других авторов появляются температура стеклования и практически универсальная безразмерная постоянная, определяемая долей флуктуационного объема, замороженной при температуре стеклования. Эта универсальная константа связана с относительной скоростью охлаждения и характерным временем изменения температуры.