Условия и методы улучшения управлений в нелинейных системах с ограничениями

Наиболее трудоемкой в стандартных методах оптимального управления является процедура варьирования управления в малой окрестности текущего приближения на каждой итерации для улучшения текущего управления. Освободиться от этой операции можно, если в данной задаче возможно построение точных формул приращения функционала, не содержащих остаточных членов разложений. Такие формулы служат основой для построения нелокальных методов улучшения управлений.

Такие формулы получены в [1] для линейных по состоянию задач оптимального управления со свободным правым концом. Улучшение достигается за счет решения двух специальных задач Коши.

В [2] методы [1] были обобщены для полиномиальных по состоянию задач оптимального управления со свободным правым концом с помощью специального представления сопряженных переменных. В этом случае улучшение управления достигается за счет решения специальной краевой задачи.

В [3; 4] методы [2] модифицируются для нелинейных по состоянию задач оптимального управления со свободным правым концом за счет представления сопряженной системы как системы дифференциальноалгебраических уравнений. В данной статье подход [3; 4] применяется для оптимизации нелинейных систем с ограничениями.

1 Постановка задачи

Рассмотрим задачу x = f (x,u,t), t G T = [t0, t1 ],(1)

x (t0) = x °,(2)

u(t) g U с Rr, t gT,(3)

Ф0(u) = ф(x(tj)) + J F(x,u,t)dt ^ min,(4)

Ф1( u) = x( x (t,) ) = 0.(5)

В задаче (1)-(5) x = ( x_t( t ), x ₂( t ),..., x n ( t )) — фазовое состояние, u = ( u 1 ( t ), u ₂( t ),..., u_r ( t )) — управляющее воздействие. Начальное состояние x ⁰ g Rⁿ задано. Функции f ( x , u , t ) и F ( x , u , t ) нелинейны и дифференцируемы по x , непрерывны по ( u , t ) на Rⁿ х U х T ; функции ф ( x ) и Х ( x ) нелинейны и дифференцируемы по x на R ” ; U с R^r — замкнутое и ограниченное множество в R^r ; значения 1 ₀, t 1 заданы.

Введем множество доступных управлений

V = { u G PC ( T ): u ( t ) G U , t G T } .

Для функции v g V обозначим x ( t , v ), t g T — решение задачи Коши (1), (2) при u = v ( t ), t g T .

Определим множество допустимых управлений

W = { u g V : x ( x ( t , , u ) ) = 0}.

Определим функцию Понтрягина

H ( p , x , u , t ) = ( p , f ( x , u , t )) - F ( x , u , t ).

Введем регулярный функционал Лагранжа

L ( u , Л ) = Ф ₀( u ) + Л Ф, ( u ), 1g R .

Отметим, что если u g W , то

L ( и , Л ) = Ф ₀( и )

(для допустимого управления функционал Лагранжа совпадает с целевым функционалом).

Введем обозначения: A _vH ( p , x , и , t ) = H ( p , x , v , t ) - H ( p , x , и , t ) (частное приращение функции Понтрягина по управлению), A _vL ( и , Л ) = L ( v , Л ) - L ( и , Л ) (приращение функционала Лагранжа).

Пусть ( и ⁰, v ) — доступные управления. Имеют место следующие точные формулы приращения функционала Лагранжа [3]

AvL(и0, Л) = -JT Av(t)H(p(t, и0, v, Л), x(t, v), и 0(t), t) dt,(6)

AvL(и0, Л) = -JT Av(t)H(p(t, v, и0, Л), x(t, и0), и0 (t), t) dt.(7)

где p ( t , и ⁰, v , Л ), t e T — решение модифицированной дифференциальноалгебраической сопряженной системы.

p = -Hx ( p, x(t, и °X и 0(tX t ) - r(tX

/ H_x ( p , x ( t , и °), и °( t ), t ) , x ( t , v ) - x ( t , и °)} + (r ( t ), x ( t , v ) - x ( t , и °)) =

'              „    /   ,       „      \(9)

= H ( p , x ( t , v ), и ( t ), t ) - H ( p , x ( t , и ), и ( t ), t ) ,

p(ti) = -^x (x (ti,и 0))- ЛXx (x (ti,и 0))- q,

( ^x ( x ( t i, и °) ) + Л/ x ( x ( 1 1, и °) ) , x ( t i, v ) - x ( t i, и °))) + qq , x ( t i, v ) - x ( 1 1, и °)) = = ф ( x ( t i, v ) ) - ф ( x ( 1 1, и ⁰ ) ) + Л ( x ( x ( t i, v ) ) - x ( x ( t i, и °) ) ) .

(ii)

Отличительной особенностью модифицированной сопряженной задачи (8)-(ii) является наличие соотношений (9) и (ii), определяющих вспомогательные величины r(t), q. В общем случае соотношения (9), (ii) можно разрешить относительно этих вспомогательных величин и свести задачу к обычной задаче Коши. Отметим, что в общем случае величины r(t), q определяются неоднозначно.

Укажем возможный вид вспомогательных величин r ( t ), q для отдельных подклассов задач.

Если все функции f, F, ф, х линейны по x (линейная по состоянию задача), нетрудно видеть, что r(t) = 0, q = 0.

В частности, если функции f, F, ф, х квадратичны по x, величины r(t), q могут быть представлены следующими соотношениями r (t) = ;2 Hxx ( p, x (t, и °), и 0( t), t)( x (t, v ) - x (t, и °) ) , q = 72 (фxx ( x (ti,и 0) ) + ЛXxx ( x (ti,и 0) )) ( x (ti,v) - x (ti,и 0) ) .

Таким образом, предлагаемый подход обобщает результаты для полиномиальных задач оптимального управления на общий нелинейный случай.

Пусть и ⁰ е W. Поставим следующую задачу (задача улучшения): найти управление v е W такое, что

Ф ( v ) <Ф ( и ⁰) ( a _v Ф ( и ⁰) <  0 ) .

Поскольку и ⁰ е W и v е W , эту задачу можно переписать в терминах функционала Лагранжа:

найти управление v е W и число к е R такие, что

A _vL ( и °, к ) <  0.

2 Подход улучшения

К решению задачи улучшения допустимого управления применим подход, основанный на применении операции проектирования.

Дополнительно предположим, что задача (1)-(5) линейна по управлению и U — выпуклое множество f (x, и, t) = A(x,t)и + b(x, t), F(x, и, t) = dd(x,t),и) + g(x, t).

Тогда функция Понтрягина с сопряженной переменной p е Rn примет вид:

H ( p , x , и , t ) = H о( p , x , t ) + H i ( p , x , t ), и ), где H о( p , x , t ) = ( p , b ( x , t )} - g ( x , t ), H i( p , x , t ) = A ( x , t ) T p - d ( x , t ). В данном подклассе задач формулы приращения (6), (7) принимают соответственно вид:

A vL ( и ⁰, к ) = - [ < H 1 ( p ( t , и ⁰, v , к ), x ( t , v ), t ), v ( t ) - и ⁰( t )) dt ,       (12)

T

A vL ( и ⁰, к ) = - [ ( H i ( p ( t , v , и °, к ), x ( t , и ⁰), t ), v ( t ) - и °( t )} dt .      (13)

T

Пусть a >  0 — фиксированный параметр (параметр проектирования).

Образуем вспомогательную вектор-функцию иа (p,x,t) = PU (и0(t) + aH 1(p,x,t)), p е Rn, x е Rn, a > 0, t е T, где PU — оператор проектирования на множество U в евклидовой норме.

Будем полагать, что множество U имеет простую структуру (параллелепипед, шар) и задача проектирования на множество U допускает ана- литическое решение.

Имеет место оценка [1]

j_r ^ H j ( p , x , t ), и a ( p , x , t ) - и ⁰( t )^ dt > — j_r || и ^а ( p , x , t ) - и ⁰( t )|| dt .

Тогда из (12), (13) и (14) следует оценка приращения функционала

A _vL ( и °, к ) < - - £ | и ^а ( p , x , t ) - и °( t )| ² dt .

Рассмотрим формулу приращения (12). Тогда нетрудно видеть, что улучшающее управление v является решением следующей системы

v ( t ) = u ^a ( p ( t , u ⁰, v , X ), x ( t , v ), t ), t g T , X g R ,         (16)

z ( x ( t i, v ) ) = 0.

Действительно, пусть управление v является решением системы (16). В силу второго равенства в системе (16) легко можно видеть, что v g W . Таким образом, на управлениях u ⁰, v функционал Лагранжа совпадает с целевым функционалом. Тогда в силу оценки (15) имеет место улучшение целевого функционала Ф ₀ с оценкой

A v Ф о( и °) <- 1 jj v ( t ) - u ⁰( t f dt .                  (17)

Для решения системы (16) при фиксированном a >  0 предлагается следующая модификация известного [5] метода простой итерации в неявной форме при к >  0

vk ^{+ 1}( t ) = u ^a ( p ( t , u ⁰, vk , X ), x ( t , vk ^{+ 1}), t ), t G T , Xg R , x ( x ( t 1, vk ^{+ 1}) ) = 0.

Начальное приближение процесса (18) — произвольное управление v ⁰ g V (которое может не быть допустимым управлением). Главной особенностью предлагаемого итерационного алгоритма является выбор параметра Xg R на каждой итерации при к >  1 для удовлетворения терминального ограничения. Предполагается, что такая возможность существует.

Приведем подробное описание итерацонного процесса (18).

Найдем решение p ^x ( t ), t g T задачи (8)-(11) при v = vk ( t ).

Пусть x ^X ( t ), t g T решение специальной задачи Коши: x = f ( x , u ^a ( p ^X ( t ), x , t ), t ) , t G T , x ( 1 0) = x °.

Найдем значение множителя Лагранжа X g R из условия

% ( x ^X ( t 1) ) = 0.                                 (19)

Cформируем управление vk+1(t) = ua (pX (t),xX (t), t) , t G T .

Замечание 1

К решению задачи (16) может также применяться следующая явная схема vk+1( t) = ua (p (t, u0, vk, X), x (t, vk), t), t G T, Xg R, x( x (t1, vk+1) ) = 0.

Для этой модификации на каждой итерации процесса (20) после вычисления решения px (t), t е T задачи (8)-(11) при v = vk (t) формируется вспомогательное управление vx (t) = ua (px (t),x(t, vk),t), t е T.

Для вспомогательного управления vx находится решение x(t, vx), t е T стандартной задачи Коши x = f (x,vX (t), t), t е T, x(10) = x0.

Значение множителя Лагранжа Хе R находится из условия х ( x ( t„ v ^x ) ) = 0.                               (21)

Для полученного решения Х е R уравнения (21) определяется следующее приближение управления vk+1(t) = Vх (t), t е T.

Аналогично конструируются итерационные процессы решения задачи о неподвижной точке на основе формулы приращения (13).

Сходимость процессов (18), (20) регулируется выбором параметра проектирования a >  0 и может быть обоснована на основе метода возмущений и принципа сжимающих отображений аналогично [2] для достаточно малых a >  0 .

Замечание 2

В задаче (1)—(5) введем в рассмотрение отображение ( H -максимизирующее отображение)

u *( p , x , t ) = argmax H ( p , x , v , t ), p е Rn , x е Rn , t е T .

v e U

Тогда на основе формул приращения (6), (7) улучшающее управление v является решением соответственно систем функциональных уравнений v (t) = u *( p (t, u0, v, Х), x (t, v), t), t е T, Хе R, x( x (t1, v) ) = 0.

v ( t ) = u *( p ( t , v , u ⁰, Х ), x ( t , u ⁰), t ), t е T , Хе R , x ( x ( t 1, v ) ) = 0.

Для решения систем (22), (23) можно использовать явные и неявные итерационные процессы, аналогичные процессам (18), (20).

3 Пример

Приведены результаты расчетов модельной задачи стабилизации вращения спутника [6] с помощью предлагаемого метода нелокального улучшения (16) на основе неявного итерационного процесса (18). Проводится сравнительный анализ эффективности указанного метода (М3) со стандартными методами условного градиента (М1) и проекции градиента (М2) [7].

Параметр a >  0, регулирующий сходимость предлагаемого метода (М3), выбирался экспериментально с точностью до порядка. Начальное значение a = 1.

Решение задач Коши осуществлялось с помощью процедуры divprk, а решение вспомогательного алгебраического уравнения — процедуры dumpol библиотеки IMSL языка Фортран [8].

Для численного решения задача [6] приводилась к форме x = — xx +100u, t g T = [0, 0.11,

x2 =

- x 1 x 3 + 25 u ₂,

x3 = - x1 x 2 +100 u 3, x1 (0) = 200, x2 (0) = 30, x3 (0) = 40, u1(t) g [-40, 40], u2(t) g [-20, 20], u3(t) g [-40, 40], t g T,

Ф ₀( u ) = 1 ( x 2(0.1) + x 2(0.1) ) ^ min,

Ф 1( u ) = x ₁(0.1) = 0.

Уравнения системы описывают динамику вращения спутника, снабженного тремя реактивными двигателями. Управления характеризуют расход топлива. Минимизируемый функционал от управления отражает цель достижения состояния, характеризующегося отсутствием вращения спутника (стабилизация).

Начальное приближение u ⁰( t ) = 0, t g T (во всех методах).

Критерий остановки

I Ф _о( uk ^{+ 1}) -Ф _о( uk )| < M ф 0( uk )|, где k — номер итерации, M = 10 ^{- 5}.

Результаты расчетов представлены в таблице.

Таблица

Метод	Ф 0	Ф1	N
М1	3.16428 х 10 - 13	2.45074 х 10 - 7	8512	0.5
М2	1.48471 х 10 - 13	3.13041 х 10 - 7	2642	0.5
М3	3.63122 х 10 - 13	5.229144 х 10 - 8	1458	10 - 5

В таблице Ф 0 — расчетное значение целевого функционала, Ф * — абсолютная величина расчетного значения ограничения, N — суммарное количество расчетных задач Коши. В последнем столбце приведены для методов М1 и М2 значения параметра штрафа, для метода М3 — значение проекционного параметра a , обеспечивающего сходимость итерационного процесса (18).

На рисунках 1–6 представлены графики полученных управлений и соответствующих фазовых траекторий (рис. 1, 2 — M1, рис. 3, 4 — M2, рис. 5, 6 — M3).

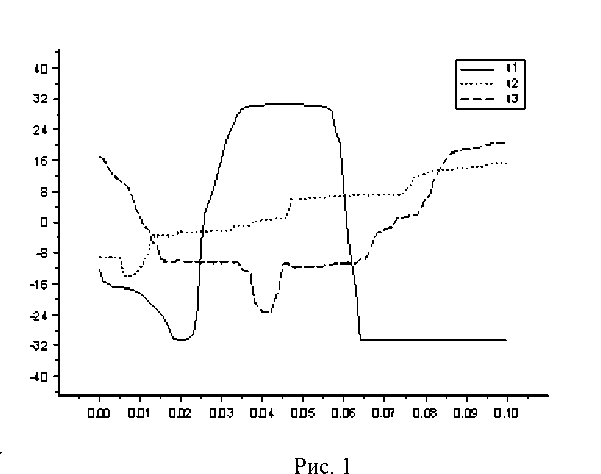
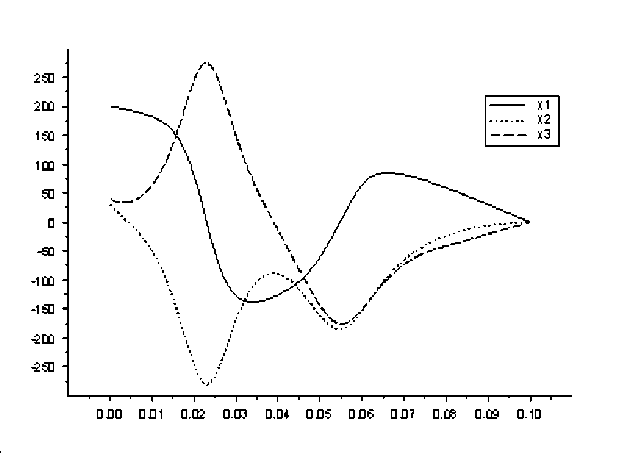
Рис. 2

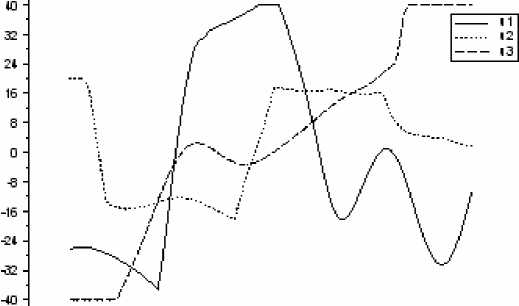
1-------1-------1-------1-------1-------1------1-------1-------1-------1-------1-------1-------1------1-------1-------1-------1-------1-------1-------1-------1-------1------Г

ООО  001  0.02 0.03 004  0£6 0.06  007  008 006  0.10

Рис. 3

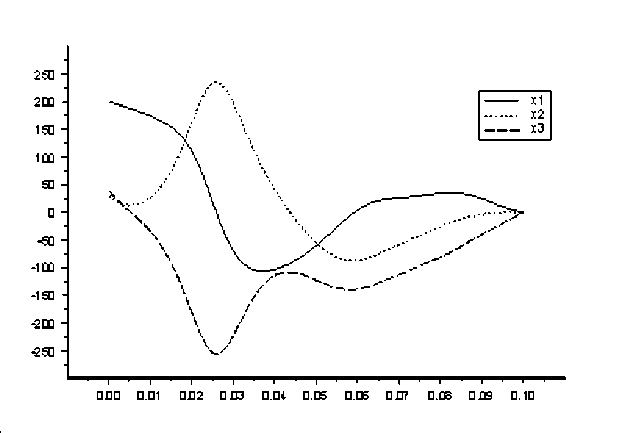
Рис. 4

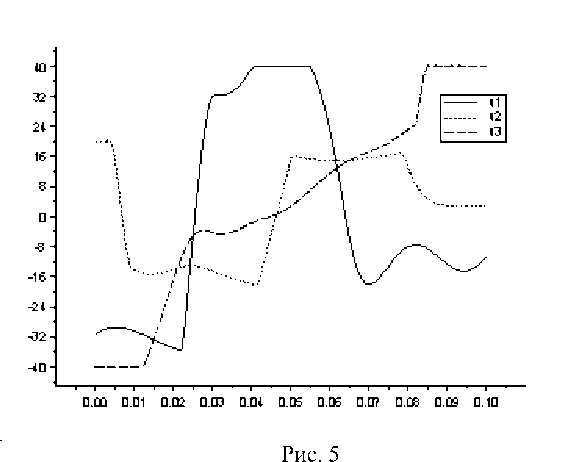
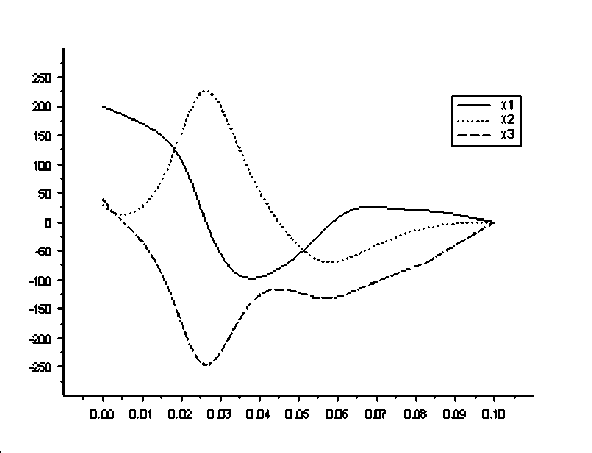
Рис. 6

Расчеты показывают, что предложенная процедура нелокального улучшения обеспечивает более точное выполнение терминального ограничения при меньшей трудоемкости.

Заключение

Предлагаемый метод свободен от операции варьирования управления и позволяет строить итерационный процесс с выполнением ограничений на каждой итерации.

Отсутствие операции варьирования управлений позволяет существенно снизить трудоемкость предлагаемого подхода по сравнению со стандартными методами.

Выполнение ограничения на каждой итерации дает возможность эффективно решать задачи улучшения допустимых управлений в отличие от стандартных методов штрафов, которые в общем случае не позволяют строить итерационный процесс на множестве допустимых управлений в задачах с ограничениями. Свойство допустимости управлений предлагаемого метода дает возможность эффективно получать приемлемые на практике управления по критерию оптимальности.