Условия параболического и гиперболического типов непараметрической поверхности

DOI:

Введение. Основные определения

В работе рассматривается произвольно заданная непараметрическая поверхность, точнее, график некоторой функции z = /(x, у),

которую будем считать достаточно гладкой и определенной для всех (x, у) Е R 2 .

Понятие типа поверхности первоначально возникло в начале прошлого века в теории двумерных римановых поверхностей и было связано со следующим известным фактом (частным случаем теоремы об униформизации): произвольная двумерная открытая односвязная поверхность (какой является заданная непараметрическая поверхность) всегда конформно отображается либо на всю плоскость R ² , либо на открытый единичный круг U 2 . В первом случае поверхность называется параболической (или имеет параболический тип ), во втором — гиперболической (или имеет гиперболический тип ).

Естественно, возник вопрос, в явном виде поставленный Л. Альфорсом в работе [4], как определить тип заданной поверхности без привлечения указанного конформного отображения. Этот вопрос стал известен в дальнейшем как «проблема типа для двумерных поверхностей».

В качестве инструмента, позволяющего определить тип поверхности, было использовано классическое, перенятое из физики, понятие емкости конденсатора на поверхности, которое, по отношению ко всей поверхности, удобно переиначить в емкость множества относительно «абсолюта» поверхности или, короче, в емкость множества на поверхности.

Понятие емкости множества может быть сформулировано не только для двумерной поверхности, но и для произвольного п-мерного (п >  2) некомпактного риманова многообразия М ^п . (Метрику многообразия для краткости не указываем.)

Назовем емкостью компакта К С Мп величину cap (К, Мп) := inf

М!12

dv ,

где inf берется по всем функциям h Е Cq ( M ^п ), таким что h ^ = 1. Здесь градиент функции h и элемент объема dv рассматриваются в метрике многообразия М ^п .

В терминах емкости определение типа произвольного п-мерного некомпактного многообразия (или поверхности) М ^п опирается на хорошо известную альтернативу:

• 1)    либо УК С М ^п :  cap (К, М ^п ) = 0,

• 2)    либо УК С М ^п :  cap (К, М ^п ) >  0.

Здесь К С М ^п — отличный от точки континуум (то есть связное компактное множество).

Тогда принимается следующее определение типа многообразия.

Определение 1. Говорят, что некомпактное многообразие М ^п в случае 1) имеет параболический тип, а в случае 2) имеет гиперболический тип .

Легко видеть, что это определение для двумерной односвязной открытой поверхности эквивалентно приведенному выше классическому определению типа поверхности, использующему конформное отображение поверхности.

Действительно, при конформном отображении двумерной поверхности значения емкости соответствующих при отображении множеств не меняются и непосредственно проверяется, что cap(^, R ² ) = 0 и cap (К, U ² ) > 0, ограничиваясь в качестве множеств К любыми замкнутыми кругами (ненулевого радиуса).

Однако при переходе от двумерного многообразия к п-мерному для определения его типа вообще нельзя использовать конформные отображения ввиду известной теоремы Лиувилля об узости класса конформных отображений в R ⁿ при п >  2.

Одним из наиболее ярких достижений в решении проблемы типа можно считать полученное S. Yau, S. Cheng, 1975 г. (см. [5]) следующее достаточное условие параболического типа для произвольного некомпактного п-мерного многообразия М ^п .

Теорема 1. Если многообразие М ^п полное и п-мерный объем 14 (г) шара радиуса г удовлетворяет условию

V   к (г)

lim —— < ос , г^+^ г то Мп имеет параболический тип.

В доказательстве этой теоремы в [5] использовалось не емкостное определение параболического типа многообразия, а эквивалентное определение типа в терминах теоремы Лиувилля для субгармонических функций на многообразии. «Емкостное» доказательство этой замечательной теоремы было получено, например, А. Григорьяном (в кандидатской диссертации 1982 г.), а в дальнейшем теорема была обобщена на случай р-емкостного типа (р >  1) многообразия в работах многих математиков.

Однако, как хорошо известно, приведенное достаточное условие параболического типа не является необходимым. Более того, существуют конкретные классы полных многообразий параболического типа, у которых п-мерный объем V_n(r) шара радиуса г растет при г ^ + с быстрее любой заданной степени г. Ниже будут приведены примеры таких двумерных многообразий.

Большой вклад в проблематику, связанную с изучением и нахождением признаков параболического и гиперболического типов поверхности (или риманова многообразия), внес Владимир Михайлович Миклюков. В работе [1] им получены различные признаки емкостного типа поверхности, как параболического (в частности, некоторая модификация признака S. Yau, S. Cheng), так и гиперболического (связанного с изопериметрической функцией поверхности) типов. Там уже сказано, что «количество работ, выполненных по этой проблеме, весьма велико и непрерывно возрастает». В поздних трудах В.М. Миклюкова (например, в [2]) содержится и современная по тому времени библиография по указанной теме.

Далее, до конца нашей работы, мы будем рассматривать только двумерные непараметрические поверхности (1). Отметим, что для таких поверхностей Дж. Милнор в работе 1977 г. [8] поставил задачу о нахождении эффективных условий параболического и гиперболического типов.

В следующих разделах мы приведем некоторые такого рода условия, дополняющие известные, содержащиеся, например, в указанных работах В.М. Миклюкова.

Прежде всего для произвольной точки (х, у) Е R 2 введем ее полярные координаты ( р , ф ), так что х = р cos ф , у = р sin ф , f (х, у) = f ( р cos ф , р sin ф ) и найдем коэффициенты метрики g tj , i,j = 1, 2, поверхности в этих координатах.

Обозначив г := {x,y,f (х,у)}, находим gii = (гр,гр) = 1 + (fP)2; gi2 = (г1,гф) = fPfф; g22 = (гфУф) = р2 + (4)2•

Здесь скобки (,) обозначают скалярное произведение в R ³ , а символ f также используется для обозначения сложной функции f ( р cos ф , р sin ф ) как функции, зависящей от ( р , ф ), то есть f = f ( р , ф ).

Тогда, применяя эти формулы, запишем для произвольной гладкой функции h на поверхности выражение для |V h | ² в метрике поверхности в полярных координатах, считая, естественным образом, что h = h( р , ф ). Поскольку

|Vh|2(р, ф) = g11^)2 + 2g12h^ + g22(h^)2 , где (g^) — обратная к (gtj) матрица, то

|v h 1 ² ( р , ф ) = 1 (( р ² + (f; ) ² )(h') ² - г/х л; л; + (i + (f р ) ² ))(л;) ² ),       (3)

g = g⁽ P^, ф ) ^:= det⁽g tj ) = р ^{2 (1} + ^{( f} P ^{) 2 )} + ^{( f ; ) 2} .                     (4)

Получим верхнюю оценку емкости (2), где в качестве множества К , отождествляя его с его прообразом в плоскости полярных координат, возьмем прямоугольник

К = { ( р , ф ) : 0 < р <  1,  0 < ф <  2 п} .

В полярных координатах определение (2) для поверхности (1) имеет следующий вид:

+∞     2π cap(K,M2 ):=infy    ар j   |Vh|2(р, ф) ^(р, ф) ^ф ,            (6)

где inf берется по всем функциям h Е C^ R ² ), таким что h ^ = 1. (При желании условие гладкости функций h можно ослабить, например, до локальной липшицевости.) Такие функции h называются допустимыми для емкости cap(K,M 2 ).

Возьмем произвольную допустимую для емкости cap(K,M 2 ) функцию h, зависящую только от р , то есть h = h( р ). Тогда из определения (6) для указанного множества (5), на основании выражений (3) и (4), следует неравенство

⁺“       ^2п         р ² + (f' ) ²

cap (К, М ² ) <      ар        . ^р ХУУ       (h ^ ) ² ^ ф .          (7)

J i   J“ ур+Ёйк + щЁ

Теперь конкретизируем допустимую функцию h( р ), определяя ее следующим образом. Зафиксируем произвольное вещественное значение г >  1 и положим

h( р ) = 1 при 0 < р <  1; h( р ) = 0 при р >  г,

Р г ^{h (} р ^{) :}= / ^ρ

dt

S^F^(t, ф ) ^аф

Г ^г        dt       \

1 / о2 ^П ^ ^{( t} , фИф/

- 1

при 1 < р <  г ,

где через F (t, ф ) обозначено (с заменой t на р )

2          ′ 2

F ( р , ф ) :=       ^{р +( / ф )} _ .

У р² (1 + (/ р ) ² ) + (/ ф ) ²

Очевидно, такая функция h( p ) действительно является допустимой для емкости указанного множества (5). Поэтому, подставляя эту функцию h( p ) в неравенство (7), после простых преобразований получаем оценку:

- 1

cap(K,M ² ) <   / -п-——---- |

1 Jo F(Р, Ф)dФ/ для любого значения г > 1. Отсюда, устремляя г ч +то, приходим к итоговой верхней оценке емкости cap(K,M2), которую, в целях удобства, сформулируем полностью в виде леммы.

Лемма 1. На непараметрической поверхности (1) рассмотрим множество K вида (5) в полярных координатах.

Тогда справедлива следующая оценка:

cap (K, M ² ) <

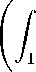
+∞ dp

0 ^{n F (} Р , ф ) ^dФ

) '

где выражение F ( р , ф ) определено в (8).

Теперь из оценки (9), в силу определения параболического типа поверхности, сразу получаем достаточное условие параболического типа поверхности (1).

Теорема 2. Предположим, что для непараметрической поверхности (1) выполняется следующее условие

Г ⁺“  [^2П       р ² + (/ ф ) ²      И- Л

‘                      ^ф --- d ф     d p = + то

1 V⁰   7 р ² (1 + (г , ) ² )+(/ф) ²

Тогда поверхность (1) имеет параболический тип.

Следствие 1. Предположим, что для непараметрической поверхности (1) выполняется следующее условие

[⁺“         d p

I  ~ч—,     =— = +^.

J ¹ J o ^ р ^{2 + ( /} ‘ ^{) 2 d}Ф

Тогда поверхность (1) имеет параболический тип.

В частности, поверхность (1) будет параболической, если величина | / ’ | растет при р ч + то не быстрее, чем р . Например, поверхность (1) в случае, когда / зависит только от ρ (то есть когда (1) — поверхность вращения), всегда имеет параболический тип, независимо от вида функции /( р ), р >  0. Тем самым, мы подтвердили высказанное выше, при обсуждении теоремы 1, утверждение, что на параболической поверхности рост объема шара (в нашем случае площади круга) радиуса г может быть сколь угодно большим при г ч + го .

2.    Достаточные условия гиперболического типа

Достаточные условия гиперболического типа поверхности (1) выведем из нижней оценки емкости множества на поверхности. Будем использовать без напоминаний или пояснений принятые в разделе 1 обозначения.

Для получения названной оценки нам потребуется следующее неравенство:

|V h | 2 >

(4) 2

i + (f p ) ² '

Это неравенство может быть получено из геометрических соображений, но легко выводится и чисто формально, исходя из формулы (3). В самом деле, выделим в правой части этой формулы (в выражении, стоящем в скобках) полный квадрат

(

_JX_ 71+W

′

h

ρ

-

C- + ч)

и отбросим его, уменьшив всю правую часть до следующего выражения

1      2,      >2,     (fP)2(fi)² A ,„,,2

g ^{( p + (f}”) ’ - I + (f p ) 2    ^{( h p )}

которое, ввиду формулы (4), совпадает с правой частью неравенства (12). Тем самым, это неравенство доказано.

Перейдем теперь к выводу нижней оценки емкости cap (K, M 2 ), где компактное множество K определено (5).

Возьмем произвольную допустимую для этой емкости функцию h = h( p , ф ), так что h = 1 при 0 < p <  1 и h = 0 при p >  г для некоторого числа г >  1.

Тогда для любого фиксированного значения ф Е [0, 2 п ]

1 = | h(r, ф )

- h(1, ф ) | < ! | h ‘ p ( p , ф ) | d p .

Отсюда, применяя к правой части неравенство Гельдера, получаем неравенство

1 <

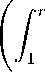
Н ( p , V )(h ' p ( p , ф )) 2^

)

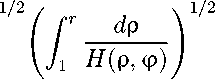
для любой непрерывной положительной функции Н ( p , ф ). Проинтегрируем обе части этого неравенства по ф Е [0,2 п ] и вновь применим неравенство Гельдера:

а                         1/2

2п       дг                                           2п       дг dф j Н(p, ф)(h/p(p, ф))2 dp     ( J^ ^ф J^

d p

Н ( p , ф )

^ 1/2

Отсюда получаем неравенство

p 2п       г^г                                     ( f2n       г^г

J   dy J Н ( p , ф )(h ^/ p ( p , ф )) ² dp >  4 n²(y    dy J

d p

Н ( p , ф )

- 1

Теперь конкретизируем функцию Н ( p , ф ), полагая

Н ( р , ф ) =

d р ² (1 + (f p ) ² ) + (Л ) ²

1 + (f p ) 2

•

Тогда, используя неравенство (12) и учитывая формулу (4) для д, из последнего неравенства приходим к оценке

/ |Vh|2 dv > 4п2( м2                        1<|p|

1 + (/;)² p²(1 + (f^ )2 ) + (fф )2

dp /ф^

-1

•

Здесь dv — элемент двумерного объема (то есть площади) данной поверхности, который в полярных координатах имеет вид dv = у/д(р, ф), где д(р, ф) указано в (4).

Наконец, из последнего неравенства, на основании определения емкости cap (К, М2) и ввиду произвольности допустимой функции h, получаем итоговую нижнюю оценку этой емкости, которую, в целях удобства, сформулируем полностью в виде леммы.

Лемма 2. На непараметрической поверхности (1) рассмотрим множество К вида (5) в полярных координатах. Тогда справедлива следующая оценка:

cap (К, М2) > 4п² ( Д

|ρ|≥1

1 + (Л )²

У^р2(1 + (Л )²) + (fф )²

dp /ф^

-1

•

Теперь из оценки (13), в силу определения гиперболического типа поверхности, сразу получаем достаточное условие такого типа поверхности (1).

Теорема 3. Предположим, что для непараметрической поверхности (1) выполняется следующее условие:

1 + (f;)2          . .    ,, dp /ф < +то • р2(1 + (^ )2 ) + (fф )2

и -|ρ|≥1

В декартовых координатах это условие имеет вид:

[I 1 + (Vf,e_p)²

---.       = dxdy < +то ,

JJlp|>i р ^1 + |Vf I^{2     9}        ’

где е_р— единичный вектор в точке (х, у), направленный вдоль радиус-вектора. Тогда поверхность (1) имеет гиперболический тип.

Следствие 2. Предположим, ются следующие условия:

что для непараметрической поверхности (1) выполня-

V(p, ф) ^:      IfPI < С < +то

для некоторого числа С и

И    ^dp^   < _+м.

ДiPi>i Д>2+7/Д

Тогда поверхность (1) имеет гиперболический тип.

Заметим, что для выполнимости условия (14) или условий (16), (17) величина |/ф| должна расти (при р ч +го) быстрее, чем р и одновременно быстрее, чем \fр|.

Близкое по форме (15) (но другое по характеру) условие гиперболического типа непараметрической двумерной поверхности получено в монографии [3, с. 240].

Рассмотрим одно применение полученных условий гиперболического типа поверхности. В конце 50-х гг. прошлого века известный специалист в теории римановых поверхностей Loewner поставил вопрос о существовании непараметрической поверхности гиперболического типа. Вскоре примеры таких поверхностей были построены несколькими крупными математиками, такими как H. Huber [7] (1959), J. Jenkins [6] (1960), R. Osserman [9] (1961). К сожалению, в этих работах (тех, которые нам удалось найти) не приводится общего условия гиперболичности типа поверхности и обоснования гиперболичности построенных поверхностей специфичны только для предложенных конструкций этих поверхностей.

Опишем конструкцию непараметрической поверхности, гиперболичность которой выводится из условий (16) и (17). Эта конструкция легко обобщается и приводит к достаточно широкому классу гиперболических непараметрических поверхностей, но для большей наглядности ограничимся лишь одним конкретным примером.

3.    Пример непараметрической поверхности гиперболического типа

Разобьем плоскость концентрическими кольцами

D(tn-i,tn) := {(х, у) G R2 : tn—i < р < tn},   D(tn,tn) := {(х, у) G R2 : tn < р < tn} , где t0 = 0 и последовательности {tn} и {tn}, п = 1, 2,..., зададим так:

~

^tn ^tn

1 + ²

-

n

,

^tn    ^tn^{+ 1} .

В кольце D(t_n-1,t_n) определим функцию f (х,у), х = р cos ф, у = р sin ф следующим образом:

f (х, у) := (р - tn-1) sin(anф) + 2(in - р) sin(an—i ф) , где a0 = 0, an = 2n п4, п = 1, 2,....

Значит, в этом кольце D(trl-1,trl) на его граничных окружностях р = tn-1 и р = tn функция f (х,у) принимает значения f (х,у)|р=tn-1

sin(an-i ф)

2n-i     ,

^{f (х,}у)\р₌1_п

sin(an ф) 2ⁿ

.

Отсюда видим, что на граничных окружностях р = t_n и р = t_n функция f (х, у) при одном и том же ф принимает одинаковые значения, равные 2^-nsin(a_nф). Поэтому в кольце D(t_n,t_n) функцию f (х,у) зададим так: f (х,у) := 2^-nsin(a_nф).

В результате функция f (х, у) корректно определена и непрерывна в R², является гладкой за исключением граничных окружностей указанных колец. При необходимости на этих стыках функцию f (х,у) можно сгладить с любой степенью гладкости. Таким образом, непараметрическая поверхность (1) построена.

Нетрудно доказать, что такая поверхность удовлетворяет условиям (16) и (17) и, следовательно, имеет гиперболический тип.