Усреднение задачи диффузии примеси из водоема в абсолютно твердый пористый грунт

DOI:

Постановка задачи

Процесс диффузии примеси из водоема в пористый грунт будем рассматривать в области Q ⁰ (водоем) и Q (пористая среда) (рис. 1), разделенных общей границей S⁰ .

*3

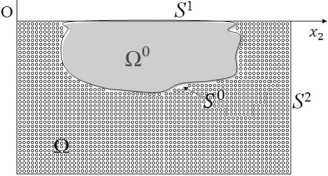
Рис. 1. Диффузия примеси из водоема в грунт

В нашем случае Ω ∈ R ² есть ограниченная область, образованная с помощью периодического повторения ячейки ε Y , где ε > 0 – малый параметр,

Y =Yf ∪Ys∪γ∪∂Y,Y =(0,1)×(0,1), εY =(0,ε)×(0,ε), где γ = ∂Yf ∩ ∂Ys – липшицева граница между множествами Yf и Ys.

ε

Через Ω f обозначим п е риодическое повторение элементарной ячейки ε Y f , а через Ω s – периодическое повторение ε Y s . Тогда

Ω = Ωεf ∪ Ωsε ∪ Γε, где Γε = ∂Ωεf ∩∂Ωεs, а область Ys окружена областью Yf (рис. 2), то есть Y s ∩ ∂Y = ∅.

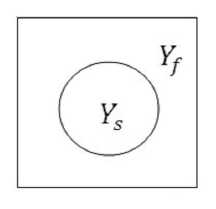
Рис. 2. Элементарная ячейка

Движение примеси в Ω ⁰ при t > 0 описывается стационарной системой уравнения:

∇⋅ P _f +ρ ( c ^ε ) e =0, P _f = α_µ D ( x , v ) - p I ,

∇⋅ v = 0,

∂ c

+ v ⋅ ∇ c = λ Δ c ,

∂ t               ^{D ,}

где ρ ( c ^ε ) = ρ _f + δ c ( x , t ); δ – положительная постоянная; ρ _f – безразмерная плотность жидкости, соотнесенная к плотности воды ρ ₀; α_µ – коэффициент вязкости; D ( x , v ) – тензор напряжений; p – давление; I – единичная матрица; c ( x , t ) – концентрация примеси; e – единичный вектор силы тяжести; λ _D – коэффициент диффузии; α_µ – коэффициент вязкости примеси v ( x , t ) =( v ₁( x , t ), v ₂( x , t )) .

Движение примеси в пористой среде Ω описывается уравнением неразрывности (2), уравнением баланса

∇⋅ P +ρ ( c ^ε )e=0, P = χ ^ε α_µ D ( x , v ^ε ) - p I ,

и уравнением диффузии примеси

ε

∂ c + v ^ε ⋅∇ c ^ε = λ Δ c ^ε ,

∂ t                  ^{D ,}

где ρ ( c ^ε )= χ^ε ( ρ _f + δ c ^ε ( x , t )).

На общей границе S ⁰ = ∂Ω ∩ ∂Ω ⁰ при t > 0 выполняются условия непрерывности

lim v ( x , t ) = lim v ^ε ( x , t ),

x → x⁰ x ∈ Ω ⁰

0 x→x x∈Ω

lim P _f ( x , t ) ⋅ n ( x ⁰ )= lim P ( x , t ) ⋅ n ( x ⁰ ), x → x ⁰                     x → x ⁰

x ∈ Ω ⁰

x ∈ Ω

где n ( x ⁰ ) есть вектор нормали к границе S ⁰ в x ⁰ ∈ S ⁰ .

Задача замыкается граничным условием Неймана на S ¹ внешней границы области Q = Ω ⁰ ∪ S ⁰ ∪ Ω при t > 0

Pf(x,t)⋅n=-p0(x,t)n, граничными условиями vε(x,t)=0,x∈S2 =S\S1,x∈Γε,t>0,(9)

∇cε(x,t)⋅n(x) =0,x∈S2 =S\S1,x∈Γε,t>0,(10)

и начальным условием

c(x,0) = c0(x), x ∈ Ω0 ∪S0.

В (1)–(11) характеристическая функция χ ^ε ( x ) области Ω ^ε _f задается выражением

x

χε(x) =ς(x)χ( ), ε где ς(x) – характеристическая функция водоема; χ(y) – характеристическая функция ячейки Yf в единичном квадрате Y.

И пусть

α _µ lim α_µ ( ε ) = µ ₀ , lim ^µ = µ ₁ . ε→ 0                 ε→ 0 ε

Целью данной работы является получение усредненных аналогов уравнений задачи (1)– (10) для случая, когда µ ₀ = 0 и 0 <  µ ₁<  ∞ . Для этого перейдем к пределу при ε → 0 .

Предположим, что S ¹ – часть оси { x ₃ = 0}, e = – e ₃, и, что область Q – подмножество полупространства { x ₃< 0}. Более того, предположим, что S ² – это гладкая поверхность и в некоторой малой окрестности плоскости { x ₃ = 0} определяется как Ф( x ₁, x ₂) = 0.

Функцию p ⁰ также положим гладкой:

(| ∇ p ⁰ ( x , t )| ² + | ∇ ( ^{∂ p 0} )( x , t )| ² ) dxdt = P ²<  ∞.

^QT                      ∂ t

Определение 1. Тройка функций {vε,cε,pε} такая, что cε ∈L2(Ωεf)∩W21,0(Ωεf), pε∈L∞(QT),vε,D(x,vε), (ζ+(1-ζ)χεf)D(x,vε)∈L2(QT), называется обобщенным решением задачи (1)–(10), если она удовлетворяет условию неразрывности (1) почти всюду в QT = Q× (0,T), граничным условиям (9), (10), начальному условию (11) и интегральному тождеству

(( ζ P f + (1 -ζ ) P ): D ( x , ϕ ) + ∇⋅ ( ϕ p ⁰ ) - ^~ ρ ( c ^ε ) e ⋅ ϕ ) dxdt =0                  (12)

QT для любых соленоидальных ϕ(x, t) = 0 при ST2 и тождеству

( 7 I c е—

J o -U f ^ d t

—

„ , Sw ^Е     „„„),, r

Vc--у — aoVc -Vv Idxdt = — Ec0 (x)v(x,0)dx d t               J        Jnf 0

для произвольной гладкой функции у ( x , t ) = 0 при t = T .

В тождестве (12) ~( c ^Е ) = ( Z + (1 — Z )) P f , а Z = Z ( x ) есть характеристическая функция области Q ⁰ в Q .

Теорема 1. Функции { v ^Е , p ^Е , c ^Е } являются обобщенным решением задачи (4), (5), (9)(11), если справедливы оценки:

0 < cЕ (x, t) < 1, x eQf, t >0,

JoTJ^ IVcЕ |2

n где C - не зависящая от e константа.

Теорема 2. Пусть обобщенным решением задачи (2)-(11) являются функции {v^Е,p^Е,c^Е}, тогда

• I)    при Е ^ 0 существует такая подпоследовательность, что:

• 1)    {v^Е} сходится слабо к v в L₂((0, T); L₂(Q));

• 2)    {V - v^Е} сходится слабо к V - v = в L₂((0,T); L₂(Q));

• 3)    {p^Е} сходится слабо кp в L₂((0,T);L2(Q));

• 4)    {c^Е} сходится слабо к c в L₂((0,T); W2(Q)) и сильно в L₂((0, T);L₂(Q)) к функции c;

• II)    функции {v, p,c} являются обобщенным решением следующей «усредненной» задачи

v =-L B(— 1Vp + P( c )e), щ m

V-v = 0,

P( c ) = (p f +5 c), m^c + v -Vc = aDV- (B(c)Vc)

dt для скорости v, давления p и концентрации примеси c в области П и П0 при t > 0, дополненной граничными условиями

v(x,t)=0, на S2 и начальным условием

|c =0, dn c (x,0) = c 0 (x), x e Q.

В (17)–(23)

m = y = JYX(y) dy есть пористость; B(c) и B – симметричные и положительно определенные постоянные матрицы, вычисляемые далее по формулам (41) и (51) соответственно; n – единичный вектор внешней нормали;

• III)    предельное давлениеp жидкости в области Q⁰ совпадает при t > 0 с гидростатическим давлением

p(x, t) = p⁰(t)-ρ_fx₃≡ p₀(x,t).                                     (24)

Доказательство теоремы 1 рассматривается в [1, с. 118].

Доказательство теоремы 2. Доказательство сильной сходимости функций c^εв L₂((0, T); L₂ (Q)) следует из оценок (14), (15), уравнения диффузии (13), леммы о компактности [3; 4] и свойств соответствующих продолжений [2]. Слабая сходимость {p^ε}, {v^ε} и {∇⋅v^ε} следует из оценки (16).

Так как усреднение модели диффузии примеси из водоема в абсолютно твердый пористый грунт на текущий момент является задачей нерешенной, проведем формальное усреднение. Для этого представим x vε = V(x, ,t)+..., ε cε =c(x,t)+εC(x,x,t)+Κ , ε pε = P(x, x,t) +..., ε где V есть 1-периодическая функция по аргументу y = x/ε.

При выводе усредненных уравнений воспользуемся предельным свойством интеграла

∫Ω ϕ (x, x,t)dxdt → ∫ (∫ ϕ (x, y,t)dy)dxdt для гладкой 1-периодической по y функции ϕ(x, y).

Переходя к пределу при (1-χε)pε = 0, для любой гладкой 1-периодической по y функции σ получим lim∫ (1-χε)pεσdxdt= ε→0 ΩT

=lim (1-χ(^x))(P(x, ^x,t) +Κ)σ(x, ^x,t)dxdt=

• ε→0 ^ΩT        ε         ε               ε

• =∫ ∫ (1-χ(y))(P(x,y,t)σ(x,y,t)dydxdt=0.

^ΩT ^Y

Перепишем P(x, y, t) в виде

P(x,y,t) =P₀(x,t)χ(y).

Тогда

p(x,t)=〈P〉Y = χ(y)P0(x,t)dy=mP0(x,t), Y откуда P(x, y, t) =1/mχ(y) p(x,t).

Определим вектор-функцию ϕ = h(x, t)ϕ₀(x/ε), равную нулю на границе S и

∇y⋅ϕ0=0.

Подставим v ^ε, p^ε в исходное уравнение и распишем каждое слагаемое, где

D(x,vε)=D(x,V(x,x,t))+1D(y,V(x,x,t))+...,

εεε а D(x, ϕ) имеет вид

D(x,ϕ)= 1(∇h(x,t)⊗ϕ0(x)+ϕ0(x)⊗∇h(x,t))+ 1h(x,t)D(y,ϕ0(x)).

• 2      εε      εε

Первое слагаемое примет вид а..

lim I Xе -^е 2 D( x ,vE): D( x, Ф) dxdt = е—0 *Ttе

= lim I" x(x)"' e^fD(x,V(x,x,t)) +¹D(y,V(x,x,t)) +J:

• e—0 jtt e e V            e e             e

: (1(V h (x, t) ® ф₀ (^x) + ф₀ (^x) ® V h (x, t)) + ¹h (x, t )D( y, Ф0 (x))) dxdt =

• 2      εε      εε

= Ho jTr h(x, t )(JYX(y)D( У, V(x y, t)):D( y, фо(у)) dy dxdt, так как

α lim   χ(x) μ ε2D(x,V(x,t)) :

e^0 ^jtt e e

: (1 (V h (x, t) ® Ф0 (x) + Ф0 (x) ® V h (x, t)) + 1 h (x, t )D( y, Ф0 (x))) dxdt = 0, 2      εε      εε

α limj X(-)^-e2Dl y,V(x,-,t) I:

e ,0 jtt e e e V

: 1¹ (Vh(x, t) ® ф₀ (^x) + ф₀ (^x) ® Vh(x, t)) Idxdt = 0,

• V 2                 e e

lim I" X(x) ^e2 D(У, V(x,x, t)): |1 h(x, t)D(У, Ф0(x)) |dxdt = e^0 ttt e e e              e V ee

T

= Ho J ^h(x, t⁾(JYX⁽У^)D(У,^V(x, y, t)):^D(y, Фо ⁽y))dydxdt.

Второе слагаемое при е — 0 будет lim I XеPе(Vh-Фо)dxdt =

E,0 ^^TT

= J J_Yx⁽y⁾P⁽x y, t^)(Vh(x t) • Ф0 (y))dyd^xdt.

Третье слагаемое при е — 0

limJ_t^xEp(c^)e-ф0^dxdt = Jo J_yX(y)h(x,t)p(c(x,t))e(x,t)-Ф0<у)dydxdt.               (31)

E ,0 T                              TaT T*Y

Собрав все слагаемые вместе, получим

J_Tr⁽JYH0^h(x, t )X⁽y^)D(У, V ⁽x y, t))^{: D(}У, Ф0 ⁽y)) dy +

+ JY x(y) P (x, y, t )V h (x, t) • Ф0<у) dy) dxdt =

= J_T^h(x t⁾⁽J_Yx⁽y)p⁽c⁽x t^))e(x t) •Ф0⁽У⁾dy)d^xdt.                          (32)

Перепишем (32) в виде

J_o^h(x t)X⁽y⁾⁽H0^D(У,^V(x y, t))^{: D(}У, Ф0 ⁽y))⁺ T t

+ — Vp (x, t) • Ф0 (y) - p⁽c (x, t ))e(x, t) • Ф0 (y)) dxdt = 0.                         (33)

m

Реинтегрируя (33), получим

^oV y • (D(y, V) - -1 Vp + p(c)e) = VyQ, y e Yf.                       (34)

m

Слагаемое V_yQ(x, y, t) в (34) возникает из-за ортогональности соленоидальных функций ф₁ в L₂(Yf) = множеству V _yQ скалярных функций Q.

Теперь перейдем к пределу в уравнении неразрывности

J_ndivv^Endxdt = £ div(v^En)dxdt—£ v^E-Vndxdt =

= I" I"    (v^E- n)ndоdt - I" v^E-Vndxdt = 0,                              (35)

J0 SSufE                    JQT для произвольной гладкой функции η = η(x, t). Подставив выражение для vε в (35), получим

JT ф, V(x, y, t) dy^ - V n(x, t) dxdt = 0.

Реинтегрируя (36), получим макроскопическое уравнение неразрывности

V- v = 0, x eO_T.                                   (37)

Проведя аналогичные рассуждения для пробной функции

η= εh(x,t)η₀(x/ε),

получим

V y - V = 0, y e Yf..

где

Будем искать решение задачи (37), (38) в виде

V = Vy^(,)zi, Q = ^Q⁽ⁱ⁾zi, i =1                     i =1

z = — (-—Vp + p( c )e), μ₀m

а функции Q⁽ⁱ⁾, V⁽ⁱ⁾являются решениями следующих периодических задач:

AyV<-) -VQ⁽ⁱ⁾= -ei,  y e Yf,

V- V⁽ⁱ⁾= 0, y e Yf, V⁽i) = 0, y e y.

Тогда

22   2

V = ^V⁽ⁱ⁾zi = ^V⁽ⁱ⁾(e_z - z) = ^(V⁽ⁱ⁾® ei)z, i=1                i=1                       i=1

учитывая, что

v = <V>Y_f

= <^(V(i) ® e,))y z i =1                      f

= B⁽f) (—(- -1 Vp + p( c )e) I

IH0 m           J

где

B=〈∑(V(i) ⊗ei)〉Y . i=1

Существование единственности решения задачи (39) и свойства матрицы

B=∑(∫YV(i)(y)dy)⊗ei=∑〈V(i)〉Yf ⊗ei(42)

i=1     f                                i=1

следует из энергетического равенства

∫ ∇V⁽ⁱ⁾:∇V^(j)dy=∫ e_i⋅V^(j)dy. Y_f                              Y_f

Лемма 1.3. Матрица B симметричная положительно определенная.

Доказательство. Пусть пороговое пространство связное и

ζ=(ζ1,ζ2),η=(η1,η2)∈R²,

22 zζ=∑ζiV⁽ⁱ⁾,zη=∑ηiV⁽ⁱ⁾.

i=1                     i=1

Тогда (42) и (43) дает нам

(Bζ)⋅η=〈zζ〉Yf ⋅η, 〈zζ〉Yf ⋅η=〈∇zζ :∇zη〉Yf, или

(Bζ)⋅η=〈∇zζ:∇zη〉Y_f,или (B^fζ)⋅ζ=〈∇zζ:∇zη〉Y_f >0.

В противном случае мы имели бы равенство

∇zζ = 0, или zζ = A⋅ y + ζ0, где A есть постоянная матрица, а ζ0 – постоянный вектор. Если принять во внимание усредненные граничные условия на γ для V (i), сделаем вывод, что zζ = 0 . Это отношение означает, что

∑ζiV⁽ⁱ⁾(y) =0,|ζ1 |²+|ζ2|²>0, i=1

а это невозможно, так как V⁽ⁱ⁾, i = 1,2 есть линейная независимая функция.

Аналогично проведем усреднение конвективного уравнения диффузии (5). Проинтегрируем и умножим уравнение на произвольную гладкую функцию ξ = 0 при t = T

χε(cε∂ξ-∇cε⋅∂wεξ-αD∇cε⋅ξ)dxdt=- εχεc0ξ|t=0dx.

ΩT      ∂t          ∂t

Проинтегрировав (41), выведем макроскопическое уравнение для концентрации

∂c m +v⋅(m∇c+〈∇yC〉Y )= αD∇ ⋅(m∇xc+ 〈∇yC〉Y )

∂t                            ff с соответствующим граничным и начальным условием

∂c

=0, x∈S, c(x,0) =mc₀(x).

∂n

Далее, взяв в качестве пробной функции в (5) функцию вида

ξ = εξ0(x,t)ξ1(x/ε), проведем аналогичные рассуждения lim L XEcE Цdxdt = lim L X(x)(c(x, t)+ e^o JQt      dt          e^oJQt E

+ eC (x,x, t) +K )-e ^(x, t )Уx) dxdt = 0, E            dtE

lim [ X^EVc^E• v^E^dxdt = lim f x(^x)(VxC(x, t) + eVyC(x,^x, t) +

E^o JQT                         E >o JQT EE

+ V yC (x, x, t ))(v(x, t) + eV(x, x, t) +K) • E^o (x, t )^1 (x) dxdt=o, εεε lim f ad xEVce •V^dxdt =

E^o *^QT г        X

= f_э ad x(-)(VxC(x,t) + VyC(:

J я T      _e

xx x-,t) + eVxC(x-,t)) X

ε

ε

X              X

X (eV^x, t M1( -) + ^(x t )V y ^( -)) dxdt = εε

x

= L I L^adХ⁽У^)(vxc^(x,t)^{+ v}yC^(x,У,t)) ^-VySiHdy L^(x, t)^dxdt,

Q-r YY

Tε lim εχεc0ξ |t=0 dx=lim εχ(x)c0(x)εξ0(x,0)ξ1(y)dx.

E >D ^JQ                    E^0 ^JQ    E

После реинтегрирования получим микроскопическое уравнение переноса концентрации

Vy • (VxC + VyC) = o, y e Yf.                                 (5o)

Таким образом, m V c + (V yC) Yf

= B^(c )V c =

к

mI + <^(VyC⁽ⁱ⁾(y)>Y_f ®ei) Vc =^f

i =1

и

B^(c) = mI + (^(vyC⁽ⁱ⁾(y))Y_f ®ei) = mI + Bo. i=1                       ^f

Усредненное конвективное уравнение примет вид m — + B(c) v •Vc = V- (a D B(c )V c).                              (52)

Предельное давление p жидкости в области Q^o совпадает при t > o с гидростатическим давлением (24).