Установление фундаментальных физических законов спроса и предложения товара "Преступление", цены преступлений, напряжения и мощности в социальных системах

Развивая теорию о спросе и предложении на товар «преступление», рассмотрим типовую задачу на основе реальных эмпирических данных, чтобы юристам, пока слабо владеющим математическими и эконометрическими методами, был понятен механизм получения соответствующих научных результатов и они смогли бы решать подобные задачи или во всяком случае понимали, как эту задачу будет решать компьютерная программа. То есть задача решается прежде всего в учебных целях с подробным обоснованием решения, чтобы колле- ги не рассматривали полученный научный результат в виде «черта, выскочившего из табакерки». В кратком и более точном виде данная задача решена мной ранее [1].

Результаты исследования

Дано: первичные статистические данные о количестве зарегистрированных в России видах преступлений и уголовных наказаниях за них в виде лишения свободы по первым частям соответствующих статей Уголовного кодекса РФ (УК РФ) за 2018 год (таблица 1).

Таблица 1.

Первичные статистические данные о количестве зарегистрированных в РФ видах преступлений в 2018 году1 и максимальных ценах на эти виды преступлений по соответствующим первым частям статей УК РФ2

Table 1.

Primary statistical data on the quality of the registered types of crimes in Russia in 2018 and maximum prices on these crimes according to the first parts of Criminal Code of the Russian Federation

Вид преступления	P лет лишения свободы (статья УК РФ)	Q зарегистрировано, штук
1	2	3
Убийство и покушение на убийство	15 (ч. 1 ст. 105 УК РФ)	8 574
Умышленное причинение тяжкого вреда здоровью (УПТВЗ)	8 (ч. 1 ст. 111 УК РФ)	23 224
Разбой	8 (ч. 1 ст. 162 УК РФ)	7 474
Грабеж	4 (ч. 1 ст. 161 УК РФ)	50 111
Кража	2 (ч. 1 ст. 158 УК РФ)	756 395
Мошенничество	2 (ч. 1 ст. 159 УК РФ)	215 036
Угон	5 (ч. 1 ст. 166 УК РФ)	19 460

1 Официальный сайт МВД России. URL: (дата обращения: 22.03.2019).

2 СПС «КонсультантПлюс». URL : (дата обращения: 22.03.2019).

Следует отметить, что в таблице 1 приведены не все структурные составляющие преступности, но охватывается 54% от общего числа зарегистрированных в 2018 году преступлений: ¹ ₁ ⁰ ₉ ⁸ ₉ ⁰ ₁ ² ₅ ⁷ ₃ ⁴ ₂∙100=54,24%, чего вполне достаточно для получения достойных внимания выводов.

Требуется: 1) установить оптимальный закон спроса на товары «преступления» в России в 2018 году (используя двойную логарифмическую модель, построить регрессию строгости наказания на количество зарегистрированных преступлений); 2) установить оптимальный закон предложения на товары преступления в России в 2018 году; 3) построить график зависимости в пакете Excel; 4) дать интерпретацию полученного уравнения; 5) проверить значимость коэффициента регрессии в полученном уравнении; 6) рассчитать коэффициент детерминации и дать его интерпретацию.

Решение: обратим внимание, что перед нами кросс-секционные (пространственные данные), то есть данные, полученные за один временной период (2018 год) по ряду объектов, которыми выступают структурные составляющие преступности.

Для параметризации уравнения парной регрессии лучше всего использовать метод наименьших квадратов (параметризация с помощью других методов даст худшие результаты, то есть большую ошибку аппроксимации).

Нам известно, что, как правило, уравнения спроса на товар «преступление» нелинейные, поэтому используем не простую линейную модель, а двойную логарифмическую модель, для чего построим новую таблицу исходных данных с логарифмическими значениями по рабочим столбцам 2 и 3.

Таблица 2.

Исходные данные из таблицы 1, представленные в натуральных логарифмах

Table 2.

Primary date of the Table 1 presented in Napierian logarithms

LN(P) LN(Q) 2,71 9,06 2,08 10,05 2,08 8,92 1,39 10,82 0,69 13,54 0,69 12,28 1,61 9,88 ное оценочное уравнение вида: Q = a–bP (крышка над Q означает оценку).

Параметр (коэффициент регрессии)          , параметр a =Q – bP, обращаем внимание, что в формулах берем соответствующие значения логарифмов, а не уровни ряда.

Строим вспомогательную таблицу:

Таблица 3.

Предварительные расчеты для вычисления параметров регрессионного уравнения

Preliminary calculations for parameter calculations of regression equation

Table 3.

LN(P)	LN(Q)	LN(P)*LN(Q)	LN(P)^2
2,71	9,06	24,53	7,33
2,08	10,05	20,90	4,32
2,08	8,92	18,55	4,32
1,39	10,82	15,00	1,92

Таблица 3.

Предварительные расчеты для вычисления параметров регрессионного уравнения

Preliminary calculations for parameter calculations of regression equation

Table 3.

0,69	13,54	9,38	0,48
0,69	12,28	8,51	0,48
1,61	9,88	15,89	2,59
1,61	10,65	16,11	3,06

В нижней строке приведены средние значения по столбцам, необходимые для вычисления коэффициента регрессии.

Рассчитываем коэффициент регрессии:

_PQ-P-Q _ 16,11 - 1,61 ■ 10,65 _ b                   3,06 - 1,612    - -2'2

Рассчит ы вае м второй параметр:

a=Q – bP = 10,65–(–2,2)∙1,61=14,2.

Записываем уравнение с логарифмами:

LN(Q) = 14,2-2,2 LN(P) .

После потенцирования получаем нелинейное уравнение:

Q = e ¹⁴,2 P -2,2 или Q = 1468864• P -2,2.

Интерпретация уравнения: если цена преступления возрастает на 1-процентный пункт, то число преступлений в среднем снижается на 2,2 процентных пункта.

Построим график зависимости.

Законы спроса и предложения на преступления в России в 2018 году

^ 200000

^ 150000

юоооо

Q= 1Е+06Р"2'2 R2 = 1

2      4      6      8      10     12     14     16

Р, лет лишен и я свободы

Рисунок 1 – Законы спроса и предложения на товары «преступления» в России в 2018 году.

Picture 1. law of demand and supply on goods "crimes" in Russia in 2018.

В программе Excel в левый столбец введем данные для переменной P, а в правом столбце через знак равенства запишем полученную функцию для переменной Q, сославшись в формуле на столбец независимой переменной. Далее выберем: «вставка», «диаграммы», «точечная», после чего встаем курсором на любую точку графика, щелкаем правой клавишей мыши, выбираем «добавить линию тренда» и в появившемся окне выбираем «степен- ная», ставим галочки для «показывать уравнение» и «поместить величину аппроксимации».

Проверим значимость коэффициентов, то есть параметров регрессионного уравнения. Для этого сначала оценим дисперсию случайной ошибки:

7     1           7

ог = sz = —Е7=1е2.

П-2  1 1

Следовательно, сначала подготовим рабочую таблицу:

Таблица 4.

Предварительные расчеты для вычисления дисперсии случайной ошибки

Table 4.

Preliminary calculations for calculating variance of random error

LN(Q)	LN(Q)	e 2
9,06	8	1,12
10,05	10	0,00
8,92	10	1,17
10,82	11	0,03
13,54	13	0,29
12,28	13	0,52
9,88	11	1,25
		4,39

Пример вычисления значений в последнем    Найдем стандартную ошибку коэффициента рестолбце: (9,06-8)2=1,12                             грессии по формуле:

σ ²= s ²= ¹ ₅ ∙4,39=0,878.                        SE(b)= L^ = ^ = 0,51.

Таблица 5.

Предварительные вычисления для расчета стандартной ошибки коэффициента регрессии

Table 5.

Preliminary calculations for calculating standard error of the regression coefficient

LN(P)	( LN ( P ) i – LN ( P ))2
2,71	1,21
2,08	0,22
2,08	0,22
1,39	0,05
0,69	0,84
0,69	0,84
1,61	0,00
	3,38

Пример вычисления: (2,71-1,61)2 =1,21.

Проверим гипотезу H₀ : переменная P не оказывает значимого влияния на переменную Q . Соответственно, альтернативная гипотеза утверждает обратное.

Вычислим расчетное значение t -статистики Стьюдента:

b -2,2

t =----=---= -4

^p SE(b) 0,51

Сравниваем расчетное значение t -статистики с табличным, приняв уровень значимости равным: α = 0,01 (1%). Число степеней свободы в нашем случае: df = n – 2 = 7 – 2 = 5.

Табличное значение t -статистики Стьюдента на 1% уровне значимости составляет 4,03, а расчетное (-4,31). Следовательно, расчетное значение по

Cov(P.Q) TQ-P-Q модулю больше табличного: |-4,31|>4,03 и нулевая гипотеза отклоняется, то есть принимается альтернативная гипотеза H1: переменная P оказывает статистически значимое влияние на переменную Q.

Можно проверить статистическую значимость свободного члена в уравнении:

SE ( a ) =

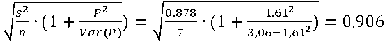
toad =-777 = ^^ = 15,67.

SE(a) 0,906

Расчетное значение больше табличного, а следовательно, коэффициент статистически значим на 1% уровне значимости.

Вычислим коэффициент корреляции ( r ) и де-терминации( R ²). Сначала рассчитаем коэффициент корреляции по формуле:

16,11 - 1,61 ■ 10,65

7з,06- 1,612 -7115,9 - 10,652

= -0,963

R 2 = - 0,9632= 0,927.

Согласно коэффициенту детерминации, 93% вариации (дисперсии) зависимой переменной объясняется вариацией независимой переменной.

Коэффициент корреляции свидетельствует, что корреляционная связь между переменными, во-первых, сильная (больше |0,7|); во-вторых, отрицательная.

Полученные результаты немного хуже точных, рассчитанных эконометрическим программным пакетом Gretl , поскольку имеют место погрешности округления.

Точное уравнение1 имеет вид:

LnQ = 13,9887-2,07838∙ LnP (0,727) (0,415)

Коэффициент детерминации R ² = 0,83 (соответственно, коэффициент корреляции: r =√ 0,83 =0,911), и уравнение в целом статистически значимо; коэффициент регрессии значим на 1 % уровне. В скобках под уравнением приведены стандартные ошибки коэффициентов.

Потенцируя, находим: Q = e ^в,9887 P -^2,07838 или Q = = 1,189∙10⁶ .

P 2,07838

Ответ: 1) оптимальный закон спроса на товары «преступления» в России в 2018 году: LN(Q) =14,2-2,2 LN ( P );

• 2)    оптимальный закон предложения на товары «преступления» в России в 2018 году: LN(Q) =14,2-2,2LN(P) (совпадает с законом спроса);

• 3)    построен график зависимости в прикладном программном пак Excel;

• 4)    интерпретация: если цена преступления возрастает на 1-процентный пункт, то число зарегистрированных преступлений в среднем снижается на 2,2- процентных пункта;

• 5)    проверить значимость коэффициента регрессии в полученном уравнении: нулевая гипотеза отклоняется, то есть принимается альтернативная гипотеза H1: переменная P оказывает статистически значимое влияние на переменную Q;

• 6)    Согласно коэффициенту детерминации, 93% вариации (дисперсии) зависимой переменной объясняется вариацией независимой переменной; коэффициент корреляции показывает, что корреляционная связь между переменными, во-первых, сильная (больше |0,7|); во-вторых, отрицательная.

2.    Устранение ранее допущенных криминологами ошибок.

Общий вывод: данная задача однозначно свидетельствует, что уровень преступности – спрос на товар «преступление» сильно и отрицательно зависит от цен, установленных на товары «преступления» при прочих равных условиях, а предложе- ние товара «преступление» совпадает со спросом, поскольку продавец и покупатель товара «преступление» – это одно и то же физическое лицо – преступник.

Ошибка 1. Ранее криминологи полагали, что преступность сдерживает прежде всего не строгость наказаний (цена преступлений), а их неотвратимость – то есть необходимость платить цену. Приведем цитату родоначальника, допустившего эту ошибку.

В середине ХVIII века в своем трактате «О преступлениях и наказаниях» (1764 г.) итальянский ученый Чезаре Беккариа писал: «Чем скорее следует наказание за преступлением, чем ближе к нему, тем оно справедливее, тем оно полезнее…одно из самых действенных средств, сдерживающих преступления, заключается не в жестокости наказаний, а в их неизбежности и, следовательно, в бдительности властей…уверенность в неизбежности хотя бы и умеренного наказания произведет всегда большее впечатление, чем страх перед другим, более жестоким наказанием, но сопровождаемый надеждой на безнаказанность. Даже самое незначительное, но неизбежное зло всегда внушает страх людям, тогда как надежда – этот дар неба, часто заменяющий все, – всегда отдаляет мысль о более жестоких наказаниях, в особенности, когда ее усиливает безнаказанность» [2]. О том же, только спустя 200 лет, пишет американский экономист, нобелевский лауреат Г.С. Беккер в своей известной статье «Преступление и наказание: экономический подход»[3].

Это ошибка, поскольку решающее значение на товарных рынках по спросу, в том числе и рынках преступности, как правило, имеет цена товара и напряжение по данной потребности (цена снижает спрос, а напряжение его увеличивает) . Но цена бывает реальной и номинальной . Неотвратимость наказания – это вероятность изобличения и наказания преступника, то есть реальная цена. Если реальная цена ниже номинальной, а на рынках преступности – это практически всегда именно так, – то более низкая цена способствует более высокому спросу, но со стороны рецидивистов, а не основной массы потенциальных преступников. Следовательно, неотвратимость наказания – это просто фактор, влияющий на цену для определенной категории потребителей, а следовательно, имеющий вторичное значение по отношению к самой цене, играющей главную роль.

Согласно ЗВППУН (закону возрастающей предельной полезности уголовных наказаний) [4]

цена преступлений особенно высока для тех, кто никогда не платил эту цену: у этих людей высок порог страха перед уголовным наказанием вне зависимости от того, насколько велика вероятность их изобличения (вероятность заплатить цену) и общая превенция спроса преступлений рассчитана на неопределенно большое количество физических лиц, ранее не привлекавшихся к реальным уголовным наказаниям. Как только физическое лицо заплатило реальную цену за совершенное преступление, уровень страха снижается и товар «преступление» становится более привлекательным. В связи с этим легко объяснить высокий уровень рецидивной преступности (из года в год в России колеблется около 30%).

Ошибка 2 состоит в том, что отрицается ценность уголовного наказания. Авторы этой ошибки утверждают, что уголовное наказание не сдерживает преступность и его следовало бы отменить.

Этой точки зрения придерживается известный российский криминолог, профессор Яков Ильич Гилинский из Санкт-Петербурга, опубликовавший статью «Наказание как результат недомыслия» [5].

Очевидно, что авторы такого подхода допускают грубейшую ошибку, поскольку при отмене всех уголовных наказаний за возможные преступления, то есть установлении на все преступления нулевых цен, это приведет к колоссальному увеличению спроса на товары преступления до естественного максимума. То есть число умышленных и неумышленных убийств, причинения тяжкого и иного вреда здоровью, изнасилований, разбоев, грабежей, краж и мошенничества резко возрастет и достигнет своего естественного максимума, что соответствует установленному мной закону спроса и предложения товара «преступление».

• 3.    Фундаментальная физическая аналогия экономического и криминологического законов спроса и предложения товара «преступление», установление фундаментальных законов спроса, предложения, цены, напряжения и мощности применительно к анализу преступного поведения.

Очевидно, что цена товара ( P ) – аналог сопротивления в гидравлической системе или электрической цепи. В физике сопротивление обычно обозначают буквой R (далее я буду использовать и то и другое обозначение). Поскольку сопротивление измеряют в омах (производные единицы в системе СИ), будем использовать аналогичное обозначение с добавлением буквы «К», то есть записывать КОм или просто КО.

Спрос (Q) аналогичен току в гидравлической системе или электрической цепи. В физике его обычно обозначают буквой I и измеряют в амперах (в системе единиц СИ силу тока относят к основ- ным единицам). Для наших целей можно записывать КА.

Уровни удовлетворения потребности ( Z ) – разница между желаемым и действительным – аналог разности потенциалов , то есть напряжения в электрической цепи или давления в гидравлической системе. В физике напряжение обычно обозначают буквой U и измеряют в вольтах (производная единица в системе СИ). Для наших целей будем записывать КВ.

Тогда спрос на товар «преступление» можно записать формулой:

Z

Q = _P (формула 1.1).

То есть спрос на товар «преступление» и любой другой нормальный товар прямо пропорционален уровню неудовлетворенности соответствующей потребности и обратно пропорционален величине цены товара, удовлетворяющего данную потребность.

Напряжение в системе определяется по формуле: Z = QP (формула 1.2).

То есть напряжение в системе личность (биосоциальное существо) прямо пропорционально произведению силы тока – спросу ( Q ) на цену товара ( P ), удовлетворяющего данную потребность. Напряжение в экономических системах удобно измерять в единицах полезности утилях или других единицах измерения, зависящих от входящих в правую часть формулы переменных.

Цена же товара определяется по формуле: P= _Q ^Z (формула 1.3).

То есть сопротивление в экономической системе прямо пропорционально уровню напряжения и обратно пропорционально силе социального (экономического) тока – спросу на данный товар.

Например, если спрос равен 5 единицам товара в месяц, цена товара составляет 5 000 рублей, то напряжение в системе личность по данной потребности составит по формуле 1.2: Z =5∙5000=25 000 штук*рублей или экономических вольт или утилей, если измерение производится в единицах полезности. Сила тока измеряется здесь в штуках или экономических (криминологических) амперах, а сопротивление измеряется в рублях или экономических омах.

Поскольку напряжение потребителей является одной из ключевых причин спроса, постольку ему следует уделить специальное внимание. Рассмотрим данный аспект более подробно.

Напряжение личности в свете удовлетворения потребностей есть суммарная разность потенциалов по существующим в ней (личности) потребностям. Например, потребность организма в воде – это разность между желаемым (или необходимым)

уровнем удовлетворения и реальным количеством воды в организме. Когда потребность в воде полностью удовлетворена, то напряжение по данной потребности равно нулю (нет разности потенциалов) и движение организма (ток) в направлении удовлетворения данной потребности отсутствует или слабо (то есть нет разности потенциалов – нет напряжения – нет движения). Направление и скорость движения личности (сила личностного тока, а значит, спрос) определяются неудовлетворенными потребностями, то есть напряжением, а кроме того, сопротивлением биологической и социальной системы относительно удовлетворения данной потребности, например, в виде уголовно-правовых запретов (товаров), то есть установленных на них цен (уголовной ответственности).

Уровень удовлетворения (напряжения) лич У ности легко описать простым уравнением: z= — (формула 1), где z - уровень удовлетворенности (напряжения) личности в единицах полезности - утилях; у - желаемое - то что нужно личности (уровень 1) в удобных единицах измерения, например, рублях; x – действительное – то, что есть, чем обладает личность в удобных единицах измерения, например, тоже рублях или других единицах измерения полезности (уровень 2); x ≠0. Очевидно, что икс не может равняться нулю, поскольку стоит в знаменателе дроби, а игрек может принимать любые значения в соответствии с принятыми единицами измерения и масштабом.

Разность потенциалов (разность двух состояний – желаемого и действительного) можно записать и функцией попроще: z=y – x (формула 2), и тогда икс может равняться нулю. Обратим внимание, что желаемое (уровень 1) стоит либо в качестве делимого – числа, подвергаемого делению, либо в качестве уменьшаемого – числа, из которого производится вычитание. Это важно, поскольку в противном случае в формуле 1 напряжение, как правило, будет принимать значения меньше единицы, а в формуле 2 отрицательные значения. Нам же из опыта известно, что желаемое, как правило (не всегда, например, при избытке чего-то), больше действительного.

Судя по формуле 1, полностью удовлетворенная потребность дает значение, равное единице:

У A z= x = в = 1, где A и B - вещественные числа, A=B, B^0, а по формуле 2 получим: z=y-x=A - B=0.

В декартовой системе координат правой ориентации X0YZ, то есть в трехмерном пространстве получим поверхность удовлетворения (напряжения) личности в зависимости от соотношения, желаемого и действительного, то есть отношения (формула 1) или разности (формула 2) уровней 1 и 2. Учиты- вая большое количество потребностей личности, легко понять, что напряжение в системе «личность» всегда присутствует, но по конкретным потребностям оно вполне может отсутствовать в согласии с законом убывающей предельной полезности (первая производная от функции совокупной полезности, описываемой параболой второго порядка, является строго убывающей линейной функцией).

Частная производная функции удовлетворения dz _ у по действительному для формулы 1: ∂x = x2 , а част-∂z ная производная по желаемому: ∂ y = x . То есть предельная норма действительного (marginal valid): dz _ у                                  /

M = -_v = о , а предельная норма желаемого ( mar ^{v ∂x x}          ∂z 1

ginal wishful): Mw= gy=x. Следовательно, точка оптимума удовлетворения достигается при равенстве предельных норм желаемого и действительного:

dz l= dz /=> 1=¹

∂x ∂y   x ² x

Очевидно, равенство предельных полезностей желаемого и действительного возмож- но лишь тогда, когда у=1 и х=1. Подставляя, имеем: ∂z ∂z 1 ∂z ∂z

_∂x /= ^∂ _∂ ^z _y =˃₁ ¹ 2 = 1 ₁ =1 =˃ ^∂ _∂ ^z _x = _∂y /=1. Именно поэтому каждый из нас всегда стремится к полному удовлетворению текущих потребностей.

Само по себе уголовное или иное наказание (цена деяния, направленного на удовлетворение потребности) есть нечто подобное сопротивлению в гидравлической или электрической цепи. Активность личности или, выражаясь языком физиков, сила личностного тока (активности личности) описывается формулой: I=z/R=(y/x)/R=1/R∙или просто: I=Ry/x(формула 3). Из формулы 3 можно получить формулу напряжения: z=IR=Ry/x∙R=(R^или просто: z=(R^2 (формула 4). Формула социального сопротивления: R = ^z |(формула 5). То есть цена в экономических и правовых системах играет примерно ту же роль, что и сопротивление в физических системах. Цена сдерживает спрос (количество приобретаемых единиц соответствующего товара), то есть активность потребителей по удовлетворению соответствующих потребностей. Ясно, что, кроме цены, в агрегированную переменную «сопротивление» входят и другие составляющие, которые пока «вынесены за скобки».

Мощность, с которой действует личность в обществе, легко описать простой формулой:

w=zI=y/x∙(y/x)/или просто: w=(R∙y (формула 5).

х R х                       X

В физике мощность измеряют в ваттах (относится к производным единицам в системе СИ).

То есть мощность личностного поведения прямо пропорциональна квадрату уровня 1 (квадрату желаемого), помноженному на величину сопротивления системы, и обратно пропорциональна квадрату уровня 2 (квадрату действительного).

Если принять за основу формулу 2, то частная производная данной функции по действительному:

∂z                                               ∂z

_∂x /= -1, а частная производная по желаемому: _∂y /= 1. То есть ^∂ _∂ ^z _x /≠ _∂ ^∂ _y ^z при любых значениях переменных икс и игрек. Поэтому, главным образом, будем пользоваться формулой 1: z = _x ^y , а не формулой 2.

Построим поверхность напряжения личности в согласии с формулой 1.

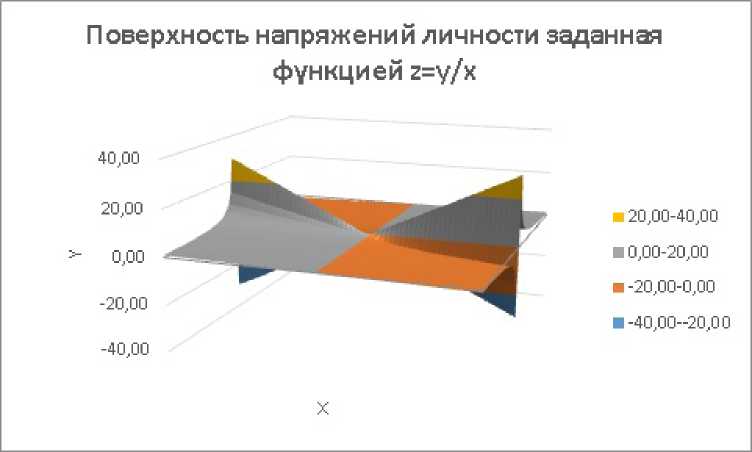
Рисунок 2 – Поверхность удовлетворения (напряжения), заданная уравнением: z = _x^y/ , где z – уровень удовлетворения, x – действительное – то, что есть; y – желаемое – то, что надо ( D _x ∊ [-3…3]; x ≠ 0; D _y ∊ [-3…3]; E _z ∊ [0 … 30][0…- 30]).

Picture 2 – The surface of satisfaction (tension) defined by the equation: z = _x ^y , where z is the level of satisfaction, x is the real – that is; y – desired – what you need ( D _x ∊ [-3…3]; x ≠ 0; D _y ∊ [-3…3]; E _z ∊ [0 … 30][0…- 30]).

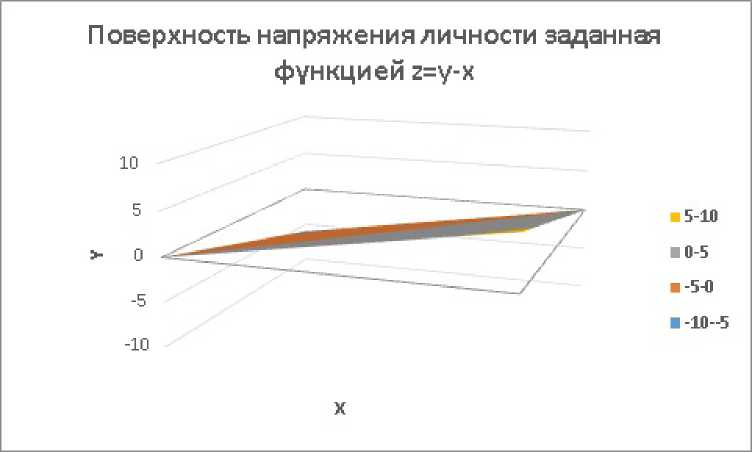
Рисунок 3 – Поверхность удовлетворения (напряжения), заданная уравнением: z = y – x , где z – уровень удовлетворения, x – действительное – то, что есть; y – желаемое – то, что надо ( D _x ∊ [-3…3]; x ≠0; D _y ∊ [-3…3]; E _z ∊ [0…30][0…-30]).

Picture 3 – The surface of satisfaction (tension) defined by the equation: z = y – x , where z is the level of satisfaction, x is the real – that is; y – desired – what is needed ( D _x ∊ [-3…3]; x ≠ 0; D _y ∊ [-3…3]; E _z ∊ [0…30][0…-30]).

Из графиков функций, представленных на рисунках 1 и 2, очевидно, что активность личности по удовлетворению потребностей возрастает по мере неудовлетворенности, то есть с ростом личностного напряжения при прочих равных условиях. Точнее – она стремится к оптимуму.

Вернемся теперь к задаче о спросе и предложении на товар «преступление» в России в 2018 году, а именно к таблице 1. Возьмем средние цену и спрос на преступность: P = 6,2857 лет лишения свободы; Q = 154325 штук, откуда среднее напряжение в российском обществе относительно товаров преступления составило в 2018 году: Z = Q∙P = = 154325∙6,2857 = 970041 штук*лет лишения свободы или просто – криминологических вольт (КВ). Соответственно, сила тока преступности составила в среднем на вид преступлений 154 325 штук или криминологических ампер (КА), а средняя цена вида преступлений составила 6,2857 лет лишения свободы или криминологических Ом (КО).

Можно посчитать напряжение по конкретным видам преступлений из той же таблицы. Возьмем, к примеру, кражи. Число зарегистрированных краж составило в 2018 году: 756 395 КА при сопротивлении (цене) краж, равном 2 КО. Следовательно, напряжение по кражам составило в России в 2018 году: Z _краж = 2∙756395 = 1512790 КВ. По разбоям: Z _разбои = 8∙7474 = 59792 КВ. То есть напряжение по кражам в 23,3 раза выше, чем по разбоям. Можно посчитать, во сколько раз напряжение по кражам выше, чем напряжение в среднем по преступности. Это можно делать, как включая кражи в общее среднее, так и исключая их оттуда.

Таблица 6.

Сводная таблица с показателями цены, спроса и напряжения в системе российского общества относительно товаров, приведенных в таблице 1

Table 6.

The summary table with indicators of price, demand and tension in the system of Russian society regarding goods, given in the Table 1

P КО	Q КА	Z КВ
15	8 574	128610
8	23 224	185792
8	7 474	59792
4	50 111	200444
2	756 395	1512790
2	215 036	430072
5	19 460	97300
Суммарное напряжение		2614800

Особо отметим, что уровень преступности, то есть спрос на товары «преступления», есть функция двух переменных: Q = f (Z, P) вида: Q = _P ^Z , подобно тому как сила тока есть функция: I = g(U,R) вида: I = _R ^U . Зная значение двух переменных, находим третью.

Таким образом, геометрически уровень преступности (спрос преступности) есть поверхность в трехмерном пространстве, заданная простым Z уравнением: Q = P . Такую поверхность легко построить вручную или задав поверхность функцией в ППП1 Excel или другой подобной программе.

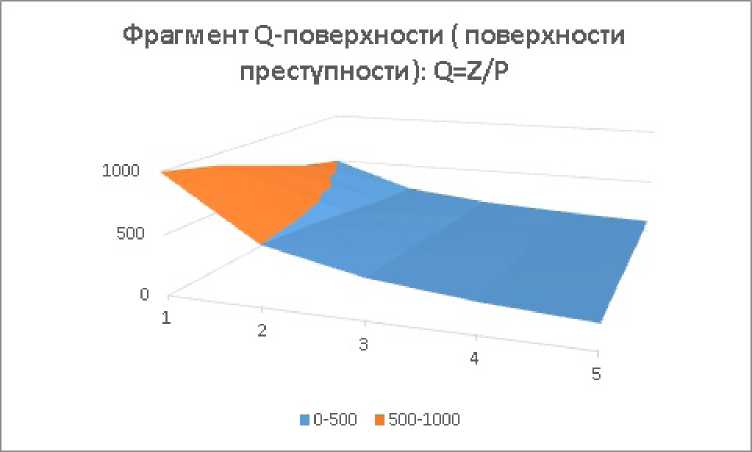
Рисунок 4 - Фрагмент Q -поверхности - поверхности преступности: Q = р ; P е [1.. .5], Z е [500.. .1000], Q е [100^1000]

Z

Picture 4 - The fragment of Q -surface - the surface of crime: Q = р ; P е [1^5], Z е [500.. .1000], Q е [100^1000]

Таблица 7.

Фрагмент дискретных значений, снятых с непрерывной поверхности преступности, представленной на вышерасположенном рисунке

Table 7.

The fragment of discrete values taken from the continuous surface of crime, presented in the above figure

Q X Z 1 P ^	1	2	3	4	5
1000	1000	500	333,33	250	200
900	900	450	300	225	180
750	750	375	250	187,5	150
600	600	300	200	150	120
500	500	250	166,667	125	100

Применение формулы Q=Z/P и ее модификации.

Говоря о спросе на обычные товары, можно применять непосредственно формулу 1.1. Например, если потребность в молоке составляет 30 литров в месяц и у вас есть 30 литров молока, то z = 0, и при любой цене молока на рынке вы покупать молоко не будете, следовательно, спрос будет равен нулю. Если же у вас 0 литров молока, а потребность 30 литров, то z = 30 - 0 = 30, и спрос на молоко будет предъявляться в зависимости от потребности на молоко, но сдерживаться ценой молока, ценой товаров-заместителей, бюджетным ограничением, то есть R - это не простая рыночная цена, а некоторая агрегированная величина, сама являющаяся функцией от ряда переменных: R = f (P, G, Рз), где P -цена товара, Pз – цены товаров-заместителей, G – бюджетное ограничение (скажем, размер пенсии или заработной платы, часть из которой вы можете потратить на молоко). Если совокупная потребность в молоке стоит 30 литров х 55 рублей = 1650 рублей в месяц, а на молоко в месяц вы можете выделить только 1000 рублей, то реально приобрести вы сможете только 1000/55=18 литров молока вместо желаемых 30-ти. Удовлетворенный спрос на молоко составит 18 литров, а неудовлетворенный 12 литров. Следовательно, в денежном выражении можно записать: Q = 1650/1000 = 33/20 = 1,65, а в количественном товарном: Q = 30/18 = 1,67. Как видно, для интерпретации эти формулы не удобны и нужно модифицировать формулу 1.1, вычитая единицу: Q=z/R-1 (формула 1.11). Тогда для нашего примера имеем: Q = 30/18-1 = 0,67, или 67 %. То есть спрос на молоко в месяц составляет 67 % от потребности с учетом сопротивления (цены товара и бюджетного ограничения), или в денежном выражении: Q =1650/1000-1=0,65, или 65% от потребно- сти. Разность в спросе между товарной и денежной формами представления объясняется в данном случае ошибками округления.

Теперь вернемся к товару «преступление». Цена товара «преступление» у нас была выражена в годах лишения свободы, и ее следует перевести в денежный эквивалент. Согласно главному закону уголовной политики – закону возрастающей предельной полезности уголовных наказаний, цена товара особенно высока для тех, кто никогда не был наказан реальным уголовным наказанием, и является субъективной оценкой. По сути, лишение свободы может быть полностью неприемлемо для данного физического лица, и тогда, сколь бы высоким не было напряжение данной личности, спрос на преступление предъявляться не будет, и можем воспользоваться для измерения спроса простой и немодифицированной формулой № 1.1: Q = z/∞ = 0. В данном случае R = ∞. C другой стороны, для рецидивистов, неоднократно отбывавших реаль- ные уголовные наказания, согласно закону возрастающей предельной полезности уголовных наказаний, сопротивление стремится к нулю и спрос на преступления является достаточно высоким. В данном случае также удобно модифицировать формулу 1.1 и в левой части уравнения ставить вероятность приобретения товара «преступление»: fffffffcccccccffff(формула 1.12). Например, если неудовлетворенная потребность составляет 20 единиц, а сопротивление равно 0,01, то получим вероятность совершения преступлений:

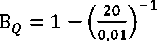
Невероятность совершения преступления данным физическим лицом: В _Q = 1 – 0,9995 = 1/2000 = 5∙10^-4. Следовательно, шансы совершения преступления данным физическим лицом составляют:

Bq 0,9995    1999      ,

= = ——  --62,5 к одному.

Bq 510—¹    32                  ^J

С другой стороны, если для данного физического лица сопротивление равно 100 КО, а напряжение равно 100 КВ, то по формуле 1.12 получим:

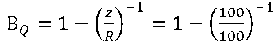
То есть умышленно в данном случае преступление совершаться не будет, поскольку вероятность умышленного преступления со стороны данного физического лица равна нулю. Однако если уровень напряжения поднимется, скажем, до 1000, а сопротивление не изменится, то получим высокую вероятность совершения преступления:

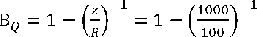
Соответственно, невероятность совершения преступления составит: ВQ = 1 – 0,9 = 0,1 и шансы совершения преступления данным физическим лицом равны BQ/(BQ ) ̅=к одному.

Bq 0,1

• 4.    Выведем фундаментальную формулу для напряжения с учетом ранее полученных по эмпирическим данным результатов. Ранее мной была получена зависимость между спросом на товар «преступление» и ценой преступлений: Q = αP ^-β , однако это лишь часть фундаментальной зависимости в реалии, определяющей спрос на преступность. Действительно, цена (сопротивление) нелинейно снижает спрос на преступления, но существует и фактор, который наращивает спрос, и он должен быть включен в фундаментальную формулу спроса на товары «преступления». Нам уже известно, что напряжение определяется формулой: Z=QP , но нам известна и формула для спроса в зависимости от цены: Q = αP ^-β . Следовательно, можно записать: Z=αP ^-β P , откуда, упрощая, получим: Z=P ^1-β α .

Зная уравнение спроса на преступность в Рос-R . „   1,189 - IO6

сии для 2018 года: ^ p 2,07838 , легко определить уровень общественного напряжения, вызвавший данную величину спроса наряду с ценами на товары «преступления»: α = 1,189∙10⁶ : β = – 2,07838 и, следовательно, для 2018 года имеем: Z = P ^{1- β} α = P ^1-2,07838 ∙ 1,189∙10⁶. Дальнейшие рассуждения тривиальны, поскольку в нашем распоряжении имеется таблица 1 с исходными данными о ценах зарегистрированных преступлений. Например, для грабежей получим нижеследующий результат вычислений: Z _{грабежи} = 4^1-2,07838 ∙ 1,189 ∙ 10⁶ = 2,666 ∙ 10⁵ Кв. Видно, что этот результат немного отличается от ранее полученного в таблице 6.

Обсуждение и заключения

Результатом проведенных вычислений стали следующие выводы:

• 1.    Общий закон спроса на товар «преступление» для любых государств в любое историческое время описывается уравнением: Q = αP ^-β либо фундаментально: Q=Z/P или Q=Py/x ; то есть уровень преступности (спрос на товар «преступление» ( Q )) сильно и положительно зависит от социального напряжения: Z (суммарно складывается из личностных напряжений), но сильно и отрицательно зависит от уровня цен (P) на товары «преступления» (уголовных наказаний), то есть является равнодействующей этих двух агрегированных сил при прочих равных условиях: Q=Z/P , что имеет чистый физический аналог: I=U/R , где I – сила тока, U – напряжение, R – сопротивление.

• 2.    Закон предложения товаров «преступления» совпадает с законом их спроса, поскольку продавец и покупатель выступают в одном лице.

• 3.    Цена товара «преступление» определяется по формуле: P=Z/Q .

• 4.    Напряжение в системе определяется по формулам:

• 5.    Мощность, с которой действует личность на рынках преступности, описывается формулой:

  

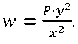
• 6.    Точка оптимума удовлетворения достигается при равенстве предельных норм желаемого и дей- dz dz    у 1

• 7.    Геометрически уровень преступности (спрос преступности) есть поверхность в трехмерном пространстве, заданная функцией (законом): Q=Z/P .

• 8.    Формулу Q=Z/P удобно модифицировать для практических целей в двух вариантах:

• 9.    С учетом формулы спроса преступности от цены получено уравнение напряжения: Z = P ^1-β α , позволяющее оценивать уровень напряжения в социально-правовых системах, зная уравнение спроса на товары преступления.

Z=QP или z = P ² y или Z=P ^1-β α .

x

ствительного:    вр аа То есть равенство ох оу    Хд X             1

предельных полезностей желаемого и действительного возможно лишь тогда, когда у = 1 и х = 1. Подставляя, имеем:

dz _ dz    1 _ 1 _     dz _ dz _ dx dy l2 1        dx dy

1)Q=£-l;2)BQ=l-gy1.