Устойчивость двухслойных рекурсивных нейронных сетей

В статье рассмотрены двухслойные нейронные сети с одинаковыми запаздываниями во взаимодействии между нейронами в сети. Такие модели имеют широкое применение в различных областях знаний.

Связи двухслойной сети с тремя нейронами в каждом слое изображены на рис. 1.

В результате линеаризации вокруг стационарного решения уравнений двухслойной нейронной сети получается линейное матричное разностное уравнение

Рис. 1: ^вухслойна^ нейронна^ сеть

x s = Y Ix s - 1 ^{+ Bx} s - k , ^s = I² - ,                    ⁽¹⁾

где x_s – вектор сигналов нейронов в момент s . Вектор x_s размерности 2 n характеризует отклонения сигналов нейронов от стационарных, I единичная 2 n х 2 n матрица, у (0 <  у <  1) коэффициент затухания колебаний нейронов, B - матрица размера 2 n х 2 n , характеризующая взаимодействия между нейронами в сети, k – запаздывание во взаимодействии между нейронами, n – число нейронов в каждом слое.

Уравнение (1) принадлежит классу матричных разностных уравнений вида:

X s = AX s - I + BX s - k , s = 1,2 -                     (2)

которые обладают важным для нас свойством: матрицы A , B могут быть приведены к треугольному виду одним преобразованием. Поэтому мы имеем возможность применить метод конуса устойчивости [4] для устойчивости этих уравнений. На основе этого метода были изучены другие нейронные сети стандартных конфигураций [1, 2, 5]. Непрерывные модели исследованы в [3].

Матрица B, например, двухслойной сети, состоящей из шести нейронов, имеет следующий вид:

^ 0  0  0  a  aa

0  0  0  a  aa

0  0  0  a  aa

b  b  b  0  00

b  b  b  0  00

v b  b  b  0  00 где a – сила воздействия нейронов первого слоя на второй, b - сила обратного воздействия.

Мы ставим задачу изучить область устойчивости системы (1) в пространстве параметров a , b при разных значениях у , n и k .

В работах [4, 6] введены конусы устойчивости для диагностирования устойчивости систем вида (2) с матрицами A , B , одновременно приводимыми к треугольному виду. Аналогичные конусы устойчивости для дифференциальных уравнений введены в [7]. Для решения задачи устойчивости двухслойных нейронных сетей нам понадобится техника конусов устойчивости, которую мы здесь изложим.

Определение 1. Конусом устойчивости для уравнения вида (2) для данного к мы называем множество точек M = (u1, u2, u3) е R3, такое, что ux + iu2 = exp(ik®') - h exp(i(к -1)®), u3 = h, где параметры h, to связаны соотношениями

0 <  h <

sin к®    n, n

---------,-- < ® < —. sin( к - 1) ® к к

Теорема 1 [4]. Пусть A,B,Sе R2nх2n и S 1 AS = AT,S 1BS = BT, где AT,BT - треугольные матрицы с диагональными элементами Xj, Pj соответственно (1 < j < 2n). Построим точки Mj = (ui j, u2 j, u3 j) е R3 (1 < j < 2n), так что u j + iu2j = pj exp(-ik argXj), u3j = | Xj |. (6)

Тогда уравнение (2) асимптотически устойчиво, если и только если все точки M j лежат внутри конуса устойчивости (4), (6) для данного к . Если некоторая точка M j лежит вне конуса устойчивости, то уравнение (2) неустойчиво.

Теорема 1 сводит задачу диагностирования устойчивости системы (2) порядка (2 n х 2 n ) к геометрической задаче в R ³ : асимптотическая устойчивость системы равносильна условию, что все точки M j (1 <  j <  2 n ) лежат внутри конуса устойчивости (4), (6) для данного к .

Для применения теории конусов устойчивости необходимо знать собственные числа матрицы B . Для матрицы B порядка 2 n собственные числа равны р 1 = р ₂ = ... = 0; р _2n - 1 =- n4ab , P 2 n = n^ab .

Определение 2. Овалом устойчивости для уравнений вида (2) для запаздывания к > 1 и параметра у мы называем кривую M (®) = (u1(®), u2(®)), такую, что u1 (®) + iu2 (®) = exp(ik®') -|у exp(i(к -1)®), где ®е (-®,®), где ® есть наименьший положительный корень уравнения । । _ sin к®

।^Y = sin( к - 1) ®"

Овал устойчивости для данного запаздывания к и данного у - это сечение конуса устойчивости (см. Определение 1) плоскостью u ₃ = У . На основании Теоремы 1 и свойств матрицы B для диагностирования устойчивости уравнения (1) достаточно проверить две точки M ( u 1 j , u ₂ j ) = u 1 j + iu ₂ j = ± n4ab (1 <  j <  2). Поэтому имеют место следующие теоремы.

Теорема 2 . Пусть даны произвольные n , к е Z ₊ , к >  1. Пусть 0 <  у <  1. Построим в R ² овал устойчивости (см. Определение 2) для данных к , у . Построим точки M j = ( u 1 j , u ₂ j ) е R ² (1 <  j <  2) так, что

• u 1 j + iu ₂ j = ± njab .

Если обе точки M j (1 <  j <  2) лежат внутри овала устойчивости, то система (1) асимптотически устойчива. В противном случае система (1) неустойчива.

Иванов С.А.

Устойчивость двухслойных рекурсивных нейронных сетей

Теорема 3 .

• 1.    Если у >  1, то система (1) неустойчива.

• 2.    Если y < 1 и 0 <  ab <  I----I , то система (1) асимптотически устойчива при любом запаз- V n J

< 1 - Y У

,                  (1 - y У дывании k . Если y < 1 и ab > I----I , то система (1) неустойчива при любом запаздывании k .

• V n J

3. Если у <  1 и ab <  0 и | ab | <

I , то система (1) асимптотически устойчива при дан- ном значении k . Если у < 1 и ab < 0 и |ab| >

I , то система неустойчива при данном sin w(y) запаздывании k . Здесь F(у,k) =-------——, где ю(у) есть наименьший неотрицательный ко- cos( k - 1)to(y)

cos k to рень уравнения y =--------- cos( k - 1) to

.

Области устойчивости системы (1) отражены на рис. 2, 3.

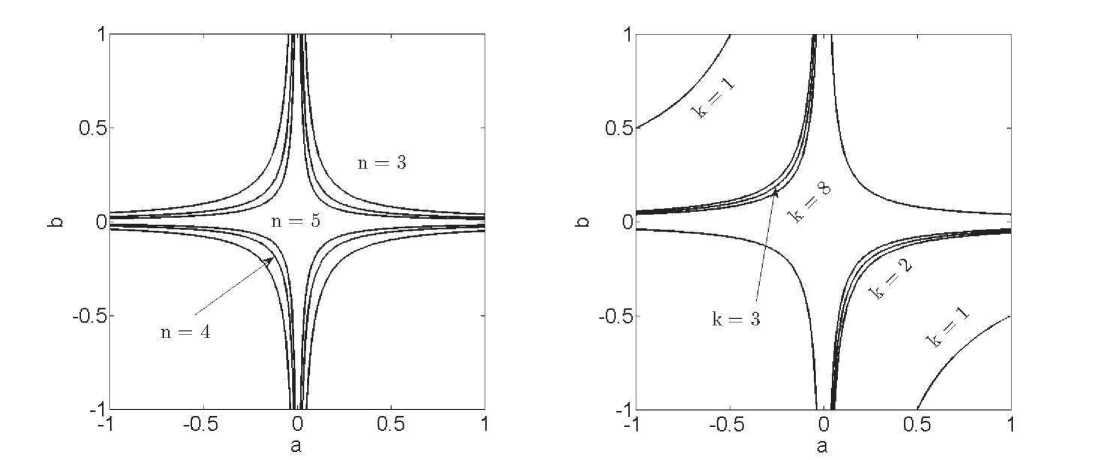
Рис. 2. Область устойчивости системы (1) в плос-           Рис. 3. Область устойчивости системы (1) в плоскости (a,b) при фиксированных y=0,4,k = 3 и              кости (a,b) при фиксированных y = 0,4,n = 3 ипе- переменном числе нейронов n                           ременном запаз^ывании k

Вывод о динамике областей устойчивости в пространстве параметров таков. С ростом числа нейронов в сети область устойчивости стягивается в крест. Но при фиксированном количестве нейронов 2 n имеется область в пространстве параметров, в которой гарантируется устойчивость независимо от запаздывания (delay-independent stability).

• 1.    Иванов, С.А. Область устойчивости в пространстве параметров рекурсивных нейронных сетей с топологией многомерного куба / С.А. Иванов // Вестник ЮУрГУ. Серия «Математика. Механика. Физика». – 2012. – Вып. 7. – №34(293). – С. 157–160.

• 2.    Иванов, С.А. Устойчивость рекурсивных нейронных сетей со звездной топологией связей / С.А. Иванов // Естественные и технические науки. – 2012. – №6(62). – С. 21–25.

• 3.    Khokhlova, T.N. Stability of a ring and linear neural networks with a large number of neurons / T.N. Khokhlova, M.M. Kipnis // Applied Mathematics and Computation. – 2012. – P. 1–14.

• 4.    Ivanov, S.A. The stability cone for a difference matrix equation with two delays / S.A. Ivanov, M.M. Kipnis, V.V. Malygina // ISRN J. Applied Mathematics. – 2011. – P. 1–19. ID 910936.

• 5.    Ivanov, S.A. Stability analysis of discrete-time neural networks with delayed interactions: torus, ring, grid, line / S.A. Ivanov, M.M. Kipnis // International Journal of Pure and Applied Math. – 2012. – Vol. 78, № 5. - P. 691-709.

• 6.    Kipnis, M.M. The stability cone for a matrix delay difference equation / M.M. Kipnis, V.V. Malygina // International Journal of Mathematics and Mathematical Sciences. – 2011. – P. 1–15. ID 860326.

• 7.    Khokhlova, T.N The stability cone for a delay differential matrix equation / T.N. Khokhlova, M.M. Kipnis, V.V. Malygina // Applied Math. Lett. – 2011. – Vol. 24. – P. 742–745.

STABILITY OF TWO-LAYER RECURSIVE NEURAL NETWORKS

• S.A. Ivanov ¹