Устойчивость одной линейной модели осциллятора с запаздывающей обратной связью
Автор: Мулюков М.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 4 (27), 2014 года.
Бесплатный доступ
Найдена новая формулировка критерия асимптотической устойчивости и устойчивости по Ляпунову одной модели линейного осциллятора с запаздывающей обратной связью. С её помощью найдены простые эффективные признаки устойчивости.
Уравнение с запаздыванием, асимптотическая устойчивость, устойчивость по ляпунову, эффективные признаки, осциллятор с запаздыванием
Короткий адрес: https://sciup.org/14729950
IDR: 14729950 | УДК: 517.929
Текст научной статьи Устойчивость одной линейной модели осциллятора с запаздывающей обратной связью
Развитие современных наук ставит пе- ред исследователями задачу расширения и усложнения традиционных моделей, в том числе – классического осциллятора. Включение запаздывания в уравнение обусловлено его принципиальным присутствием в механизмах обратной связи и биологических объектах. В данной работе изучается устойчивость урав- нения
x ( t ) + kx (t ) + k,X( t ) + k3x ( t - h ) = f ( t ), t > 0,
1 2 3 (1)
X(t) = y(t), t g [-h; 0), где h > 0, k 1, k2, k3 g ^, и f, у - локально суммируемые функции.
Вопрос об устойчивости уравнения (1) или его обобщений рассматривался неоднократно. Критерий устойчивости, по-види-мому, был впервые получен в работах [1], [2]. Однако граница области устойчивости в используемых авторами координатах состоит из счётного множества криволинейных поверхностей, которые достаточно сложно анализировать. В данной работе показано, что можно выбрать сечения этой области таким образом,
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 13-01-96050 р_урал_a).
что её граница в этом сечении состоит только из прямолинейных сегментов.
В работах [3], [4], [5] рассматривается обобщение уравнения (1), для него показано, что в зависимости от коэффициентов уравнения возможны три случая:
-
а) уравнение устойчиво при любых значениях запаздывания;
-
б) уравнение не является устойчивым при любых значениях запаздывания;
-
в) при увеличении запаздывания до некоторой величины h * < от происходит чередование устойчивых и неустойчивых режимов, а при h > h * уравнение (1) не является устойчивым.
Ниже мы повторим эти результаты, основываясь на простых геометрических соображениях.
В работах [6], [7] тоже рассматривается обобщение уравнения (1); для него найдены достаточные признаки устойчивости и неустойчивости как в терминах коэффициентов уравнения, так и в терминах корней тригонометрических многочленов.
Под решением задачи (1) будем понимать функцию с абсолютно непрерывной производной, удовлетворяющую уравнению (1) почти всюду. Как известно, любое решение представимо в виде x (t) = x (0) X1 (t) + x (0) X 2 (t) + j X 2( t - s) g (s) ds, 0
где g ( s ) = f ( s ) + k з у( s - h ) x ( s - h ), X — функция Хевисайда, а X 1 ( t ), X 2 ( t ) – фундаментальные решения , определяемые как решения однородной задачи (1) с нулевой начальной функцией и начальными условиями X 1 (0) = X 2 (0) = 1 , X 1 (0) = X 2 (0) = 0 [8], [9], [10, c.12–31], [11].
Однородное уравнение (1) будем называть устойчивым по Ляпунову , если оба его фундаментальных решения ограничены.
Однородное уравнение (1) будем называть асимптотически устойчивым , если оба его фундаментальных решения стремятся к нулю при t ^ от .
Вследствие автономности уравнения (1), асимптотическая устойчивость для него совпадает с экспоненциальной, которая, согласно теореме Боля–Перрона, равносильна устойчивости по правой части из пространства f g Lp , p > 1 [10, c.103-107, 127-142], [11], [12], [13], [14].
Такая постановка задачи согласуется с традиционной, где под решением уравнения (1) понимают продолжение начальной функции, предполагаемой непрерывной [15].
Исследование устойчивости уравнения (1) сводится к изучению расположения в комплексной плоскости корней характеристического квазиполинома
F ( z ) = a + p z + v ze - z + z 2 , z g □ , (2) где a = k 1 h 2 , p = k 2 h , v = k 3 h . Как известно, асимптотическая устойчивость (1) эквивалентна отрицательности вещественных частей корней (2) [16, с. 209]. Квазиполиномы, обладающие таким свойством, будем называть устойчивыми .
Устойчивость по Ляпунову уравнения (1) эквивалентна тому, что у квазиполинома (2) отсутствуют корни с положительной вещественной частью, а все мнимые корни просты [16, с.210].
Обозначим ф— j = A 0 = 0 и
Ф n = пn + arccos I (-1) n + 1 —I, n g □ 0 (3) I v J
A n =ф n - 1 ф n = п 2 n 2 - arccos I (-1) n + 1 — I, n g □ . k v J
Пусть z g^ . Тогда lim F(z) = +от , z ^+от а F(0) = a ; следовательно, при a < 0 квазиполином (2) имеет неотрицательный вещественный корень, т.е. не является устойчивым.
Теорема 1. Пусть a > 0 . Тогда
-
• если — > |v| , то уравнение (1) асимптотически устойчиво;
-
• если — < -|v| , то уравнение (1) не является асимптотически устойчивым;
-
• если — = v , то (1) асимптотически устойчиво тогда и только тогда, когда — > 0 и Va/ ( 2п ) не является целым числом;
-
• если — = -v , то (1) асимптотически устойчиво тогда и только тогда, когда — > 0 и (T a - п ) Д 2п ) не является целым числом;
-
• если |—| < |v|, то для асимптотической устойчивости уравнения (1) необходимо и достаточно выполнения неравенства
ф n 7 v 2 -— 2 < ( ф П -a )( - 1) n sgnv , (4)
при aG ( A n , A n + 1 ] .
Доказательство. Воспользуемся методом D -разбиений [17, с.124–130] и найдём поверхность в пространстве параметров коэффициентов квазиполинома, на которой F имеет мнимый корень z = i ф . Эта поверхность определяется системой
a +vф sin ф = ф2,
1 а (5)
—Ф +vф cos ф = 0, где параметр ф меняется на множестве [0, от).
Далее рассмотрим три множества, которые определяются этой системой.
-
1. При ф = 0 система определяет плоскость a = 0 , на которой имеем
-
2. При v = 0, ф^ 0 система (5) определяет луч а > 0, ц = 0 .
-
3. Пусть ф, v ^ 0 . Обозначим r = ц/v . Перепишем второе уравнение системы (5) в виде r = — cos ф и рассмотрим три возможных случая.
F ( z ) = zq 0 ( z ) , где q 0 ( z ) = —+ v e z + z .
При переходе через эту плоскость по направлению возрастания a корень z = 0 приобретает отрицательную вещественную часть. При этом если q0 устойчив, критерий чего хорошо известен [18], то при достаточно малом положительном а квазиполином F тоже устойчив.
Если | r | > 1 , то данное уравнение не имеет решений, и F не имеет корней на мнимой оси.
Если | r | = 1 , то (5) определяет прямые а = п 2 n 2, r = (—1) n + 1 , n e □ 0 , на каждой из которых F имеет мнимый корень z = i п n .
Пусть | r | < 1 . Разрешив второе уравнение системы (5) относительно ф , получаем формулу (3).
Так как sin фп =(—1)n 41 — r2 , то из первого равенства в (5) имеем:
а + v(—1) n ф n 4 1 — r 2 =ф 2 , n e □ o . (6)
Равенство (6) вместе со случаями 1, 2 определяют набор прямых в плоскости r = const .
Таким образом, мы построили поверхность, которая разбивает пространство параметров квазиполинома на области, в которых он имеет одинаковое количество корней с положительной вещественной частью.
Поэтому при | r | > 1 количество таких корней квазиполинома F и многочлена а + ц г + z 2 совпадает.
Аналогично рассматривается случай | r | = 1 : квазиполином F устойчив при ц = v ( —1 ) n + 1 > 0, а ^ п 2 n 2. Наконец, при | r | < 1 прямые образуют счётное множество треугольников, примыкающих к положительной полуоси а . Для некоторых значений r они изображены на рис. 1–4.
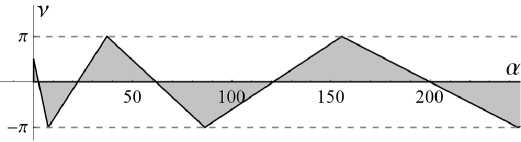
Рис. 1. Сечение области устойчивости плоскостью r = 0
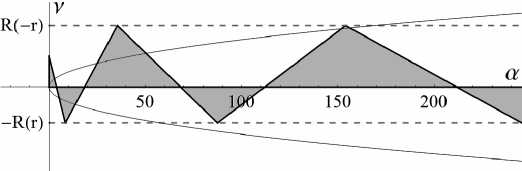
Рис. 2. Сечение области устойчивости плоскостью r = 0.4
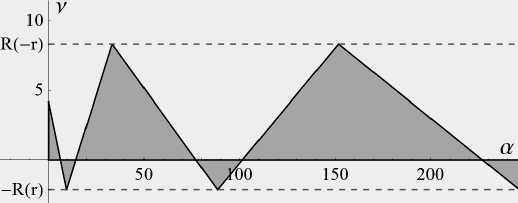
Рис. 3. Сечение области устойчивости плоскостью r = 0.8
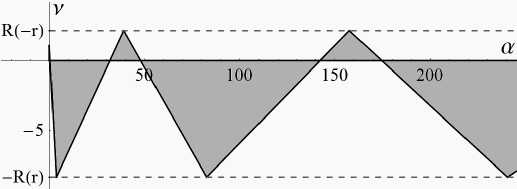
Рис. 4. Сечение области устойчивости плоскостью r = — 0.8
В частности, при r = 0 они являются областью устойчивости квазиполинома а + v ze — z + z 2, [17, с.129], [19]. Опишем эти треугольники подробно. Первый из них – прямоугольный, отсекающий от осей v, а отрезки arccos(— r )/ 4- — r 2 и arccos 2 (— r ) соответственно. Основания треугольников находятся на оси а и представляют собой отрезки |^ф 2 — 1 , ф П J , n еЫ 0 . Вершины треугольников под номерами n > 2 находятся в точках { A n — 1 , (—1) n — 1 R ( (—1) nr ) } , где
R ( r ) = 2arccos ( r )/ 71 — r 2.
Следовательно, треугольники расположены в полуполосе
—R(r)
Докажем, что описанные выше треугольники являются сечением области устой- чивости квазиполинома (2) при любых r < 1.
По теореме об обратной функции знак приращения вещественной части корня на линиях (6) вдоль оси а совпадает со знаком выражения [20, c. 137]
- Re
F d а
F z
■= i Ф n
Уф n sin Ф n
F z 2
d а.
Из этого следует, что вне этих треугольников нет точек области устойчивости. А поскольку каждый треугольник с рис. 1 непрерывно переходит в соответствующий треугольник при изменении r , то в силу непрерывной зависимости расположения корней квазиполинома от параметров, данные треугольники (и только они) принадлежат области устойчивости. □
Граница области асимптотической устойчивости при ае [ 0;100 ] изображена на рис. 5.
В итоге имеем следующее утверждение.
Теорема 2. Пусть к 1 , h > 0 . Тогда
-
• если k 2 > | k зЬ то уравнение (1) асимптотически устойчиво;
-
• если к 2 <-| k 3| , то уравнение (1) не является асимптотически устойчивым;
-
• если к 2 = к 3 , то (1) асимптотически устойчиво тогда и только тогда, когда к 2 > 0 , но h ^ 2пnk—m , n е^ 0 ;
-
• если к 2 = - к 3 , то (1) асимптотически устойчиво тогда и только тогда, когда к 2 > 0 , но h ^ п(2 n +1) к 1 - 1/2, n g^ 0 ;
-
• если I к 2| < | к з| , то для асимптотической устойчивости уравнения (1) необходимо и достаточно выполнения неравенств h +- 1 < h < h n , где n = 2 m при v >| p | , n = 2 m +1 при v < -1 p | , m e^ 0 , и
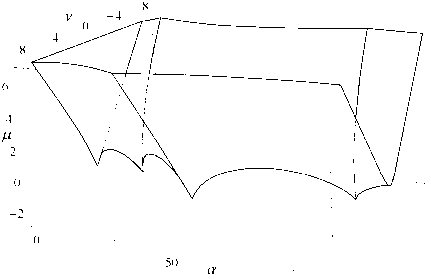
Рис. 5. Область асимптотической устойчивости уравнения (1)
h ± = ф n т n
± дУ кз2 + к | + дУ 4 к1 + к2 - к22
2 k 1
причём h* = h - , а n * определим следующим образом: при к 3 > | к 2| это наибольшее чётное число, а при к 3 < - | к 2| наибольшее нечётное,
удовлетворяющее неравенству
* n
< — п
k v + arccos k2
k 2
k
Найденное представление существенно упрощает анализ области устойчивости. Изучим картину смены устойчивых и неустойчивых режимов при изменении величины h . Зафиксировав k 1 , k 2 , k 3 , мы определяем параболу а = к 1 у 2 / к 3 2 в плоскости r = к 2 / к 3 . На рис. 2 изображена парабола а = 9v 2. Ясно, что если эта парабола проходит слева от вершины треугольника, то её пересечение с треугольником порождает "устойчивый" интервал запаздывания, который можно найти, выразив h в явном виде из (4).
Для того чтобы найти величину h * достаточно указать наибольший номер вершины, находящейся слева от параболы.
Проведенный выше анализ позволяет находить простые достаточные признаки устойчивости и неустойчивости. В качестве примера приведем два следствия.
Следствие 1. Пусть | к 3| > | к 2| . Для того чтобы уравнение (1) было асимптотически устойчивым, необходимо выполнение неравенств к 1 > 0 и
0 < h
—
Г к2
< к3 У
k
+ arccos 2 <п k 3
Доказательство. Мы ограничились случаем | r | < 1 . Неравенства (7) и (8) эквивалентны. □
Следствие 2. Уравнение (1) асимптотически устойчиво при любых положительных h и k 1 тогда и только тогда, когда k 2 > | k 3 1.
Следствиям 1 и 2 можно дать графическую интерпретацию. Уравнение (1) асимптотически устойчиво, если точка { v, ц } находится выше закрашенной области на рис. 6, и не является асимптотически устойчивым, если точка расположена ниже этой области.
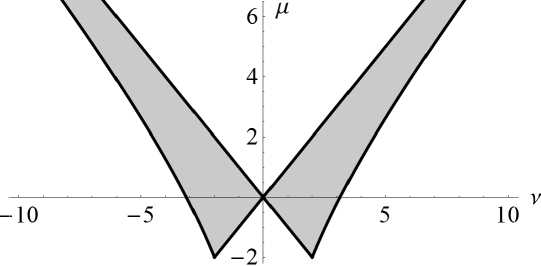
Рис. 6. Графическая интерпретация следствий 1, 2
В заключение рассмотрим поведение корней квазиполинома (2) на границе области асимптотической устойчивости. Найдём условие, при котором у квазиполинома есть кратный корень на мнимой оси: F ( i ф) = F X i ф) = 0 . Из F ( i ф) - i ф F '( i ф) = а - ф 2 (v e - i ф — 1) = 0 имеем v sin ф = 0 и а = ф 2 ( v(—1) n — 1 ) . В силу F '( i ф) = 0 при ф = 0 имеем прямую а = ц + v = 0 , а при ф = п n > 0 точки —ц = v(—1) n = 2 . За исключением этих точек и плоскости а = 0 квазиполином F имеет на границе только простые комплексно-сопряжённые корни. Таким образом, для уравнения (1) доказан критерий устойчивости по Ляпунову.
Теорема 3. Для того чтобы система (1) была устойчива по Ляпунову необходимо и достаточно, чтобы точка { а, v, ц } принадлежала замыканию области асимптотической устойчивости, описанной в теореме 1, за исключением прямой а = ц + v = 0 и точек { п 2 n 2,2(—1) n , — 2 } , n еК 0 .
Список литературы Устойчивость одной линейной модели осциллятора с запаздывающей обратной связью
- Hsu C.S., Bhatt S.J. Stability charts for second-order dynamical systems with time lag. 1966. J. Appl. Mech. 33 (1). P. 113-118.
- Hsu C.S., Bhatt S.J. Stability charts for second-order dynamical systems with time lag. 1966. J. Appl. Mech. 33 (1). P. 119-124.
- Сооке K.L., Grossman Z. Discrete Delay, distributed delay and stability switches. 1982. J. Math. Anal. Appl., 86. P. 592-627.
- Campbell S.A. Stability and bifurcation in the harmonic oscillator with multiple, delayed feedback loops//Dynamics of continuous discrete and impulsive systems. 1999. № 5. P.225-235.
- MalaMiovsh E., Mirhn L. On stability of second-order quasi-polynomials with a single delay. Automatica 42. 2006. С. 1041-1047.
- Cahlon B., Schmidt D. Stability criteria for certain second-order delay differential equations, Dynamics of continuous discrete and impulsive systems. Series. A: Mathematical Analysis. 2003. 10. P. 593-621.
- Cahlon B., Schmidt D. Stability criteria for certain second-order delay differential equations with mixed coefficients//Journal of Computational and Applied Mathematics. 2004. 170. P. 79-102.
- Азбелев Н.В., Максимов В.П., Рахматуллина Л.Ф. Введение в теорию функционально-дифференциальных уравнений. М.: Наука. 1991. С. 8-20.
- Азбелев Н.В., Симонов П.М. Устойчивость уравнений с запаздывающим аргументом//Изв. вузов. Математика. 1997. № 6. С.3-15.
- Азбелев Н.В., Симонов П.М. Устойчивость решений уравнений с обыкновенными производными. Пермь: Изд-во Перм. ун-та, 2001.
- Азбелев Н.В., Березанский Л.М., Симонов П.М. и др. Устойчивость линейных систем с последействием. I//Дифференциальные уравнения. 1987. Т. 23, № 5. С. 745-754.
- Азбелев Н.В., Березанский Л.М., Симонов П.М. и др. Устойчивость линейных систем с последействием. II//Дифференциальные уравнения. 1991. Т. 27, № 4. С. 555-562.
- Азбелев Н.В., Березанский Л.М., Симонов П.М. и др. Устойчивость линейных систем с последействием. III//Дифференциальные уравнения. 1991. Т. 27, № 10. С. 16591668.
- Азбелев Н.В., Березанский Л.М., Симонов П.М. и др. Устойчивость линейных систем с последействием. IV//Дифференциальные уравнения. 1993. Т. 29, № 2. С. 196-204.
- Хейл Дж. Теория функционально-дифференциальных уравнений. М.: Мир, 1984.
- Беллман Р., Кук К.Л. Дифференциально-разностные уравнения. М.: Мир, 1967.
- Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных уравнений с отклоняющимся аргументом. М.: Наука, 1971.
- Андронов А.А., Майер А.Т. Простейшие линейные системы с запаздыванием//Автоматика и телемеханика, 1946. 7 (2, 3). С. 95106.
- Мулюков М.В. Об асимптотической устойчивости двупараметрических систем дифференциальных уравнений с запаздыванием//Изв. вузов. Матем. 2014. № 6. С.48-55.
- Постников М.М. Устойчивые многочлены. 2-е изд.//Едиториал УРСС. М., 2004.


