Вероятностный подход к управлению многостадийными многокритериальными технологическими процессами

Производственный процесс – упорядоченная, регулярная последовательность взаимосвязанных технологических процедур, которая превращает исходные ресурсы в конечные продукты. До середины 80-х годов ХХ века процесс производства представлялся вторичным по отношению к конечному продукту, т.е. на предприятиях существовал продуктовый подход. В настоящее же время любой производственный процесс рассматривается как основное средство получения прибыли и повышения конкурентоспособности, иными словами, доминирующим становится процессный подход.

При процессном подходе производство конечного продукта представляется сетью связанных между собой технологических стадий, в ходе которых осуществляется преобразование входных ресурсов в выходную продукцию, при этом стабильный, точно исполняемый, высококачественный технологический процесс наиболее эффективно и с минимальными затратами обеспечивает получение продукции запланированного качества. Примером может служить организация хлебопекарного производства [1].

Хлебопекарная отрасль пищевой промышленности по праву занимает особое место в производстве продуктов питания, так как хлеб в России традиционно является основным продуктом питания. А поскольку почти 40 % суточной нормы калорий человек получает от потребления хлеба, то актуальность интенсификации технологических процессов хлебопекарного производства очевидны.

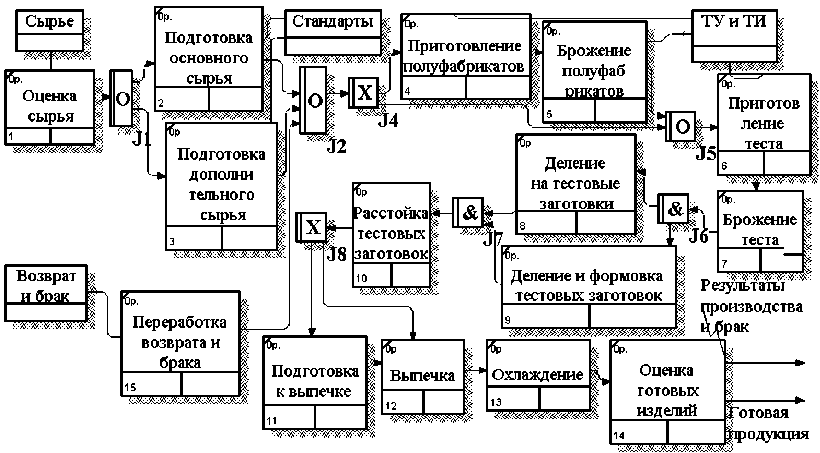
Характерной особенностью современного периода является критический подход к технологии приготовления теста непрерывным способом и восстановление классической технологии, что позволяет улучшить вкусовые качества хлеба, усилить его аромат, дольше сохранить свежесть. Создание продукта является процессом, подлежащим управлению, с целью получения требуемых качественных показателей конечного изделия. Это предполагает установление параметров, характеризующих и определяющих весь ход производства, которые изменяют процесс, приводя его в соответствие с технологическим регламентом. Определение данных параметров достигается в результате декомпозиции процессов, в виде горизонтальных структур, на отдельные взаимосвязанные подпроцессы, каждый из которых является определенным технологическим переделом (рисунок 1).

заготовки

Расстойка сырья заготовок ротовая

Результаты..... производства цррак

Сырье

Оценка сырья

Возврат и брак

ТУ нТИ тестовых

Охлаждение ^

Выпечка

Подготовка к выпечке

Оценка готовых изделий

. Деление и формовка тестовых заготовок

Приготов . ление

Переработка " возврата и брака

Подготовка

■ дополни тельного

| Брожение

| полуфаб

| рикатов

^         |— Стандарты

Подготовка |---

. основного ими»

я* Приготовление 1 полуф абрикатов

Деление на тестовые

I Брожение

I J6 теста

Рисунок 1. IDEF3-диаграмма «Производство изделий» Figure 1. IDEF3-diagram "Production of goods"

Существует большое число методов управления качеством. К наиболее часто применяемым методам можно отнести структурирование функции качества, анализ последствий и причин отказов, статистические методы, ABC – метод и др. [2]. Одним из новых и перспективных способов управления качеством технологических процессов является вероятностный метод, предложенный в [3] и позволяющий определять повышение вероятности выпуска качественных изделий в пределах ресурсов, выделенных на мероприятия по улучшению уровня качества.

Каждая из стадий, представленных на рисунке 1, имеет некоторую вероятность качественного завершения. Но, если при неудовлетворительном выполнении операций по подготовке основного и дополнительного сырья, переработки и возврата брака, оценке готовых изделий, сырье и продукция дальнейшим производственным действиям не подвергается (т.е. идет возврат), то при некачественном выполнении стадий по приготовлению полуфабрикатов, теста, расстойки тестовых заготовок и их выпечке выход не отбраковывается, а подлежит дальнейшей переработке, согласно технологическим инструкциям на данный вид изделия. Поэтому требуется проводить ряд мероприятий с целью улучшения качественного выполнения всех технологических операций.

Наиболее рациональное распределение производственных ресурсов, используемых для проведения необходимых организационнотехнических мероприятий, возможно при раздельном управлении качеством на каждой стадии. Это позволяет определить приоритетные направления развития всего производства, осуществление которых улучшает одну или несколько компонент показателя P конечн – вероятности качественного завершения всего технологического процесса.

Обозначим P i j – вероятность того, что на i-й стадии процесса в результате проведения j-го мероприятия качество промежуточного или конечного продукта повысится до необходимого уровня. Данные вероятности можно получить либо посредством моделирования технологического процесса, либо экспериментально как отношение числа случаев получения качественного продукта к общему числу случаев.

Согласно известной формуле теории вероятностей, вероятность того, что к конечной стадии будет получен качественный продукт, равна произведению «промежуточных» вероятностей. Тогда имеем формулу:

N р = п р *, конечн           ij* , i=1

где j* – номера мероприятий, выбираемых (производимых) на каждой стадии. Очевидно, что номера j* надо выбирать, исходя из максимального значения конечной вероятности.

Любой технологический процесс многокритериален. Концепция управления качеством на основе вероятностного подхода для многошаговых процессов заключается в том, что в качестве одного из основных критериев принимается вероятность выпуска качественного изделия Pконечн. Однако очевидно, что реализация тех или иных мероприятий по повышению Pконечн предполагает подключение определённых ресурсов, что, в первую очередь, неизбежно связано с некими денежными затратами. Таким образом, приходим к задаче оптимального управления, имеющей, как минимум, два критерия – вероятность качественного завершения технологического процесса, которую надо максимизировать, и суммарные затраты на проведение корректирующих мероприятий, которые надо минимизировать.

Для разработки принципиальной модели оптимального управления рассмотрим простейший случай, когда одно мероприятие оказывает влияние только на одну стадию. Введем для каждой i -й стадии вектор zi = (zi 1, zi 2,-, zin, ), i = 1,..., N ,           (2)

каждая компонента которого может принимать значение 0 или 1.

• 1 1, если u - е мероприятие проводится для i - й стадии , 7- = 4 ziu 1

• [ 0 в противном случае

Обозначим c iu – материальные затраты, связанные с проведением u - го мероприятия на i- й стадии процесса. Необходимо определить набор мероприятий с минимальной суммарной стоимостью, который обеспечивает достаточный уровень вероятности качественного завершения всего производственного процесса, в котором стадии последовательно зависимы.

В общем случае на каждой стадии можно проводить не одно, а целый комплекс из n i мероприятий. Очевидно, что суммарная стоимость этих комплексов будет равна сумме отдельных составляющих. Следовательно, в общем случае в качестве второго критерия эффективности технологического процесса необходимо использовать целевую функцию вида

N n i

• q 2 = ^^ z iu c u ^ min ⁽³⁾ i = 1 u = 1

С другой стороны, понятно, что повышение вероятности качественного завершения каждой стадии в общем случае не связано простой линейной зависимостью с набором проводимых мероприятий. Поэтому надо иметь такую модель, которая позволяла бы установить связь между комплексом реализуемых мероприятий и достигнутым уровнем вероятности качественного завершения каждой стадии. Иными словами, модель должна реализовывать некое множественно-точечное отображение вида:

_Ф : 2 ^{ z u U { P ij* },               (4)

где 2 ^{ z^{iu }} - множество всех подмножеств мероприятий, каждый элемент которого образует некоторый комплекс М i j* мероприятий, реализуемых на i-й стадии процесса; P i j* –вероятность качественного завершения i-й стадии после реализации комплекса М i j* . Благодаря модели (4) появляется возможность связать вероятности, соответствующие первому критерию эффективности процесса с переменными z i u , определяющими значения второго критерия.

При оптимизации структуры многостадийного технологического процесса хорошо зарекомендовало себя применение теории графов. Тогда оптимальная последовательность проводимых мероприятий будет ассоциироваться с оптимальным путём в графе, описывающем структуру процесса. Определённая сложность для оптимизации состоит в том, что при поиске оптимального пути критерий должен быть аддитивным. Тогда значение критерия на всём пути будет равно сумме значений критерия на дугах, составляющих оптимальный путь, а это не соответствует формуле (1). Однако формулу (1) можно почленно прологарифмировать и получить необходимый вид критерия:

N ln Pконечн = ∑lnPij* (5) i=1

В качестве метода оптимизации будем использовать частный случай векторного алгоритма Флойда-Уоршалла [4], когда исходный граф не содержит контура. Это позволяет избежать одного внешнего цикла, что существенно повышает быстродействие алгоритма.

Рассмотрим в качестве примера, иллюстрирующего работу алгоритма, следующую задачу. Имеем двухстадийный технологический процесс, на каждой стадии которого возможно проведение любого комплекса из трёх мероприятий, включая «пустого» комплекса, при котором мероприятия вообще отсутствуют и процесс пущен «на самотёк». Следовательно, на каждой стадии возможно реализовать по 8 комплексов мероприятий:

∅ , z1, z2, z3, z1 ∪ z2, …, z1 ∪ z2 ∪ z3. Пронумеруем возможные состояния процесса числами от 1 до 18, где 1-е состояние – начальное, 18-е – конечное (они фиксированы). После реализации какого-либо комплекса мероприятий на первой стадии процесс может прийти в одно из состояний с номерами 2 – 9. А после реализации какого-либо комплекса мероприятий на второй стадии процесс может прийти в одно из состояний с номерами 10 – 17.

В таблице 1 приведен фрагмент матрицы двумерных весов дуг графа, соответствующих различным переходам из одного состояния в другое на 1 и 2 стадиях (всего граф содержит 80 дуг и, соответственно, 64 варианта путей).

Таблица 1

Фрагмент матрицы двумерных весов дуг графа

Table 1

Fragment of the matrix of two-dimensional weights of graph arcs

Начальная вершина дуги | Initial vertex of arc ( i )	Конечная вершина дуги | Final vertex of the arc ( j )	Вероятность P ij достижения нужного качества | The probability of achieving the required quality	Затраты на проведение комплекса мероприятий | Costs of the complex of activities
1	2	0,75	0,0
1	3	0,85	7,0
1	4	0,90	12,0
1	5	0,88	10,0
1	6	1,00	19,0
1	7	1,00	22,0
1	8	0,98	17,0
1	9	1,00	29,0
2	10	0,68	0,0
2	11	0,78	5,0
2	12	0,83	15,0
2	13	0,81	20,0
2	14	0,93	20,0
2	15	0,94	35,0
2	16	0,91	25,0
2	17	0,98	40,0

Реализация алгоритма позволила найти 16 Парето-оптимальных путей в данном графе из вершины №1 в вершину № 18:

Rout 1 = 1 6  17  18 Rout 2 = 1 8  17  18 Rout 3 = 1 6  15  18

Rout 9 = 1 2 11 18 Rout 10 = 1 3 11 18 Rout 11 = 1 4 11 18

Rout 4 =	1	3	14	18	Rout 12 =	1	5	11	18
Rout 5 =	1	4	14	18	Rout 13 =	1	6	11	18
Rout 6 =	1	5	14	18	Rout 14 =	1	8	11	18
Rout 7 =	1	6	14	18	Rout 15 =	1	2	10	18
Rout 8 =	1	8	14	18	Rout 16 =	1	5	10	18

Соответствующие значения  1-го и

2- критериев приведены в таблице 2.

Таблица 2

Значения критериев эффективности технологического процесса

Table 2

Values of the efficiency criteria of the technological process

№ пути | Path number	Значение q 1 | Value of q 1	Значение q 2 | Value of q 2	№ пути | Path number	Значение q 1 | Value of q 1	Значение q 2 | Value of q 2
1	0,9800	59,0	9	0,5850	5,0
2	0,9604	57,0	10	0,6630	12,0
3	0,9400	54,0	11	0,7020	17,0
4	0,7905	27,0	12	0,6864	15,0
5	0,8370	32,0	13	0,7800	24,0
6	0,8184	30,0	14	0,7644	22,0
7	0,9300	39,0	15	0,51	0,0
8	0,9114	37,0	16	0,5984	10,0

На рисунке 2 приведено графическое пред- оси абсцисс 1-го критерия изменено на проти-ставление таблицы 2 (для наглядности направление      воположное).

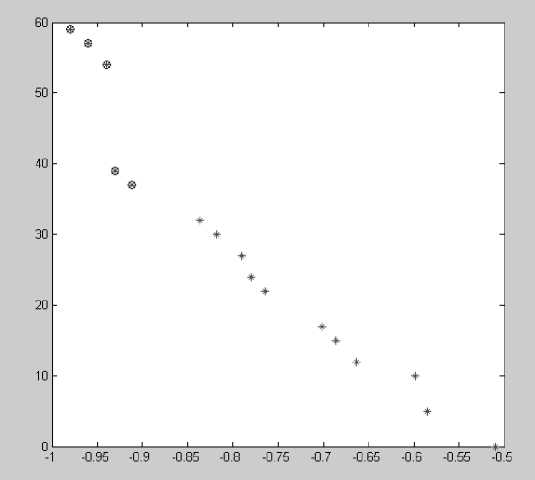
Рисунок 2. Множество Парето-оптимальных решений двухстадийного технологического процесса (синим кругом обозначены решения со значением вероятности качественного завершения процесса более 0,9)

Figure 2. The set of Pareto-optimal solutions of the two-stage production process (the blue circle marked solutions with the value of probability qualitative completion of the process more than 0.9)

Вывод

Применение векторной оптимизации на графах позволяет получить развёрнутую картину последствий различных вариантов управления на каждой стадии технологического процесса, ЛИТЕРАТУРА

• 1    Федюкин В. К. Управление качеством производственных процессов. М.: КНОРУС, 2013. 332 с.

• 2    Авсеева О. В., Медведкова И. Е., Скляров В. А. Экспертная оценка функций отклика в задаче управления качеством многошаговых технологических процессов // Сборник статей II Международной научно-практической интернет-конференции «Моделирование энергоинформационных процессов» Воронеж, 22 – 24 декабря 2014. Воронеж, 2015. С. 84 – 89.

которую затем можно будет использовать для технологической подготовки производства либо для оперативного управления функционированием технологического процесса.

3 Авсеева О.В., Говорский А.Э., Тебекин Ю. Б., Кравец О. Я. К постановке задачи оптимизации проектирования систем специальной связи // Информационные технологии моделирования и управления. 2009.

№ 7(59). С. 945 – 948.

• 4    Блинов И.В., Бугаев Ю.В., Чикунов С.В. Обобщение алгоритма Флойда-Уоршалла на случай нескольких критериев // Вестник Тамбовского государственного технического университета. 2009. Т. 15. № 4. С. 885 – 892.