Вихревая гидродинамика: новый подход к моделированию геосистем
Автор: Гунин В.И.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (40), 2018 года.
Бесплатный доступ
Для вхождения в эру устойчивого развития необходимо научиться управлять природой, т.е. оптимизировать ее влияние на человека и ее отклик на антропогенные воздействия. Для этого нужно уметь моделировать все природные процессы, а также научиться прогнозировать их развитие во времени и пространстве, постепенно вводя элементы управления. Как известно, все природные процессы в той или иной степени связаны с вихревыми гидродинамическими потоками, вызванными перераспределением вещества в гравитационном поле. Используя математический аппарат, базирующийся на системе уравнений Навье-Стокса, сложно описать вихревые (кольцевые) структуры, формирующиеся во всех геосферах нашей планеты под действием гравитационного поля. Предложен математический аппарат вихревой гидродинамики (ВГ), основанный на новом фундаментальном свойстве гравитационного поля - векторном потенциале, для которого rotA ≠ 0, позволяющий адекватно описывать вихревые структуры и глубже понимать их сущность. С помощью анализа системы уравнений (ВГ) и результатов, полученных при решении ряда задач, сделаны обобщения по некоторым физическим процессам и явлениям, распространенным в различных геосферах Земли.
Гравитация, векторный потенциал, конвекция, вихревые структуры, математическая модель, численный эксперимент, тепломассоперенос, мантия, литосфера, кора, плюм, диапир, рифт
Короткий адрес: https://sciup.org/147245356
IDR: 147245356 | УДК: 551.24:550.31:556.013:532.50: | DOI: 10.17072/1993-0550-2018-1-5-18
Текст научной статьи Вихревая гидродинамика: новый подход к моделированию геосистем
В последние десятилетия активно развивается идея (концепция) устойчивого развития. Существует множество определений и трактовок этой концепции, но ни политики, ни экономисты, ни философы, разработавшие эти определения, до сих пор не могут понять и объяснить суть этой концепции, она становится просто модной теорией для управленческой "элиты". Некоторые страны уже считают, что вышли на путь устойчивого развития. В России объявлен даже конкурс "Регионы – устойчивое развитие". Но природа своей непредсказуемостью, стихийные бедствия, терроризм, экономические кризисы, войны и др. расставляют все на свои места.
С математической точки зрения суть концепции устойчивого развития – это оптимальное управление природой т. е. необходи-
мо предсказать событие (явление), спрогнозировать его развитие и оптимизировать последствия его воздействия. Под термином природа понимается вся окружающая среда, включая человека. Это минимаксная задача в результате решения которой при минимальном воздействии на окружающую среду можно получить от нее максимальную пользу. Для выполнения этого, на первый взгляд простого определения, необходимо проделать громадную работу, которая по времени займет десятилетия или даже столетия. Необходимо разработать математические модели всех процессов, проходящих в окружающей среде и связи между ними, научиться их прогнозировать во времени и пространстве, а затем постепенно, изучая и корректируя, вводить элементы управления этими процессами.
Для моделирования процессов в окружающей среде нужны адекватные математические модели и эффективные численные методы. На наш взгляд, необходимо использо- вать разные подходы для описания и решения этих задач, что в свою очередь позволит глубже изучить и понять природные явления и более точно определить направление движения к истине. Только тогда можно будет говорить о начале вхождения в эру устойчивого развития.
Ни для кого не секрет, что весь наш мир, все, что нас окружает, и мы сами находимся под воздействием гравитации. Все процессы, протекающие в природе, в той или иной степени связаны с гидродинамическими потоками, вызванными перераспределением вещества в гравитационном поле. Основной силой переноса вещества в природе является конвекция, которая в свою очередь зависит от сил, вызванных какими-то внешними воздей- ствиями (вынужденная конвекция), и внутренних сил, вызванных плотностными неоднородностями, возникающими за счет градиентов температуры и концентрации вещества (свободная конвекция).
Вихревые, кольцевые структуры довольно широко распространены во всех геосферах Земли и космическом пространстве. Особенно ясно это стало при дешифровке космических снимков в конце XX в. Размеры этих структур могут достигать сотен километров. Считается, что в земной коре данные структуры контролируют крупные месторождения металлов и других полезных ископаемых, а в гидросфере и атмосфере являются основными переносчиками энергии и вещества.

Рис. 1. Вихревые структуры, образованные при формировании Земной коры
В земной коре вихревыми называют такие структуры, в которых существенная роль принадлежит спиралевидным, дугообразным и эксцентричным кольцевым формам. В этих структурах всегда присутствуют две морфологически различные части: меньшая – внутренняя, и большая – внешняя. Внутренняя часть (часто округлой формы) занимает не более одной пятой, а нередко – меньше одной десятой всей площади структуры, и может

Рис. 2. Вихревые (кольцевые) структуры, а – в атмосфере, б – на льду озера Байкал (космический снимок)
Генезис вихревых, кольцевых структур пока не ясен. Существует множество гипотез их образования от вращательно-поступатель- располагаться как в ее центре, так и эксцентрично. Внешняя часть структур очерчена спиралевидными (вихревыми) или полуколь-цевыми (дуговыми) формами различной кривизны, которые обязательно сходятся к центру внутренней изометричной части. Как правило, эти структуры продолжаются и на глубину, в этом случае их называют винтовыми структурами.
ного внедрения магмы до космического ударно-метеоритного. Многие связывают образование структур с вращательными движениями блоков земной коры в горизонтальном направлении. В большинстве случаев в центре или в пределах данных структур фиксируются интрузивные тела, которые, скорее всего, и являются причиной образования вихревых, кольцевых и винтовых структур, но механизм формирования условий для их образования пока остается дискуссионным [2] (рис. 1).
С другой стороны, в атмосфере и гидросфере все мы явно наблюдаем различные вихревые структуры – циклоны, антициклоны, торнадо, бора и тому подобное. Это позволяет предположить, что и все вихревые структуры, связанные с глубинными процессами, развиваются по тому же сценарию, что и на поверхности Земли (рис. 2).
Но до сих пор эти процессы, идущие во всех оболочках Земли, недостаточно изучены, так как для описания и моделирования вихревых структур нет адекватного математического аппарата.
Используемые методы, проблемы: новый подход
Для описания гидродинамики в задачах со свободной и вынужденной конвекцией в сплошных (вязких) и пористых средах широко используется система уравнений Навье–Стокса, в которой эти силы описываются совместно – одним уравнением. Это приводит к трудностям при ее решении, так как она не является системой типа Коши–Ковалевской, т. е., нет эволюционного уравнения для давления. Имеются и другие особенности, возникающие при использовании численных методов решения данной системы уравнений, например наличие малого параметра при второй производной может приводить к существенному изменению гладкости решения, и ряд других.
Уравнения Навье–Стокса, вытекающие из уравнения Больцмана, полученного на основе уравнений механики и статистики, непосредственно описывают только ламинарные течения, поэтому с помощью этой системы уравнений сложно, а в большей части невозможно описать вихревые структуры, которые формируются в гравитационном поле во всех средах при возникновении плотностной стратификации.
Для описания вихревых структур (турбулентности), привлекают дополнительные гипотезы и предположения, которые повышают степень этой системы уравнений, запутывают физический смысл вихревых процес- сов и усложняют численные методы решения задач.
Для избавления от этих недостатков существует подход, основанный на исключении давления из уравнений за счет применения операции ротор ( rot ) к уравнению для вектора скорости, и переходу описания скоростей через функцию тока и вихрь. Такой переход повышает порядок дифференциального уравнения по пространственным переменным, но за счет введения функции тока дает автоматическое удовлетворение уравнения неразрывности, при этом система уравнений усложняется и обычно решается раздельным – двухполевым методом. Приравнивание операции ротора скорости к вихрю (которые по определению тождественно равны) не позволяет вычислить функцию тока через другую независимую функцию, что приводит к новым такого же порядка трудностям, связанным с заданием граничных условий для вихря [10].
Поэтому возникает необходимость в построении новой математической модели, позволяющей избежать указанных затруднений. Для вычисления функции тока и затем определения через нее вектора скорости можно использовать независимую векторную функцию – генератор вихрей . Похожий метод использовался некоторыми исследователями для решения задач в пористых средах, но только для двумерных уравнений [9].
В 1999 г. автором был разработан математический аппарат трехмерной Вихревой Гидродинамики ( ВГ) для пористых сред, который затем был обобщен и для вязких сред. Предлагаемый новый математический аппарат основан на расщеплении конвекции на две составляющие – свободную, вызванную градиентом плотности и записанную через векторную функцию тока Ψ – векторный потенциал , и вынужденную, вызванную источниками , записанную через скалярную функцию U – скалярный потенциал, что позволяет раздельно вычислить их значения, а затем получить параметры суммарного конвективного потока.
На базе этого математического аппарата автором разработан пакет программ на языке Fortran, с помощью которого можно решать широкий круг трехмерных задач тепломассо-переноса в пористых и вязких средах на персональных компьютерах.
За последние годы были получены решения для ряда теоретических и практических задач, которые опубликованы в цен- тральных журналах РАН, доложены на Российских и международных конференциях.
В данной работе сделан вывод системы уравнений вихревой гидродинамики и дано обоснование предлагаемого подхода. На анализе результатов решения задач тепломассо-переноса в пористых и вязких средах показаны возможности информационной технологии, разработанной на основе ( ВГ) и сделаны обобщения по некоторым физическим процессам и явлениям, распространенным в различных геосферах Земли.
Обоснование нового подхода и вывод уравнений (ВГ)
Из теории поля известно, что любое векторное поле M можно разложить на две составляющие. M = M 1 + M 2 . Поле M 1 = grad U – источниковое или дивергентное поле , где U – произвольная функция, имеющая первую производную, и выполняется равенство rot grad U = 0. Функцию U называют скалярным потенциалом векторного поля M . Тогда, div M 1 = div grad U = k 1 δ , ⇒ ∇ 2 U = Δ U = k 1 δ , где k 1 – константа пропорциональности, δ – плотность источников.
Поле M 2 = rot A – вихревое или циркуляционное поле , тогда, div rot A = 0. Функцию A называют векторным потенциалом векторного поля M . Существует бесконечное число векторных функций A , описывающих одно и то же поле M , такие функции могут отличаться друг от друга с точностью до градиента некоторой скалярной функции ϕ , так как rot grad ϕ = 0. Это приводит к следующему соотношению: rot rot A = k 2 W ⇒ grad div A - ∇ 2A = k 2 W. Так как существует бесконечное множество функций A, описывающих одно и то же поле M , то можно выбрать из них такое, которое удовлетворяет равенству div A = 0 ( калибровка Кулона ) ⇒ ∇ 2A = Δ A = k 2 W , где k 2 – константа пропорциональности, W – вектор плотности вихревых линий (линий тока), а плотность (густота) линий векторного поля пропорциональна его интенсивности.
Все процессы, протекающие в природе, в той или иной степени связаны с гидродинамическими потоками, вызванными перераспределением вещества в гравитационном поле. Известно, что генератором свободной конвекции является неоднородность плотности среды, а интенсивность конвекции пропорциональна градиенту этой плотности [1]. Значит, векторную функцию W можно представить в виде градиента скалярной функции, например ρ (плотность среды), тогда W = gradρ. Свободно конвективные потоки вещества, вызванные градиентом плотности, формирующим гидродинамический диполь, удобно записать с помощью векторной функции тока Ψ – векторный потенциал, а потоки вынужденной конвекции, вызванные источниками, через функцию U – скалярный потенциал (давление, напор).
Тогда перенос среды (вещества) можно записать в виде векторного уравнения Пуассона Δ U = k1 δ , описывающего источниковое или дивергентное поле, записанное через скалярную функцию U и ΔΨ = k 2 ∇ ρ – описывающее вихревое или циркуляционное поле, записанное через векторную функцию Ψ , которое в декартовой (ортогональной) системе координат распадается на три скалярных уравнения инвариантных относительно системы координат:
ΔΨ x = k 2 ∂ρ / ∂ x, ΔΨ y = k 2 ∂ρ / ∂ y,
ΔΨ z = k 2 ∂ρ / ∂ z. (1)
В общем случае векторное поле скоростей, вызванное источниками и генераторами вихрей, можно записать так:
V = V 1 + V 2 = grad U + rot Ψ . (2) Это равенство представляет собой одну из форм теоремы Гельмгольца.
На этом основании автором предложена новая трехмерная система уравнений, позволяющая разделить конвекцию на две составляющие – свободную и вынужденную – и, вычислив их значения, получить параметры суммарного конвективного потока. Эту систему можно записать так:
ΔΨ = k 2 ∇ ρ ; (3)
Δ U = k 1 δ ; (4)
V = grad U + rot Ψ . (5) Система уравнений (3–5) представляет собой систему уравнений Вихревой Гидродинамики (ВГ) , записанную в векторной форме.
В общем случае плотность может зависеть от потенциальной функции ρ =F(U), т.е. от внешнего воздействия, но это достаточно узкий класс задач. В поле гравитации в основном формируются свободно-конвективные потоки, и плотность зависит от других скалярных функций – температуры и концентрации вещества ρ =F(T,C), для описания полей которых вводятся дополнительные уравнения.
Предлагаемый подход хотя и увеличивает порядок системы уравнений в частных про- изводных по сравнению с системой уравнений Навье–Стокса, но позволяет более точно вычислить конвективную составляющую V, которая играет определяющую роль в задачах гидродинамики и вычислении полей температуры и концентрации вещества, в задачах теп-ломассопереноса. Для решения задач со свободноконвективными течениями уравнение (4) можно исключить, и порядок системы уравнений понизится. Кроме того, система (ВГ) является классической системой уравнений в частных производных эллиптического типа и позволяет более эффективно использовать вычислительные методы для ее решения.
При выводе уравнения для векторного потенциала использовалась калибровка Кулона, но существует другой подход, в котором используется калибровка Лоренца (его часто применяют при выводе уравнения для векторного потенциала в электродинамике). Если использовать калибровку Лоренца, то в уравнении появляется дополнительный член, а при нем – коэффициент (волновое число), который для задач гидродинамики сложно определить и, скорее всего, он должен быть разным для каждой задачи, что усложнит их решение. В дальнейшем, возможно, для каких-то задач гидродинамики такой подход может быть использован.
Данную систему уравнений также можно использовать для решения задач электромагнитной динамики, через векторный и скалярный потенциалы определять напряженность электрического или магнитного поля, используя их коэффициенты сопротивления или проводимости. Так как все напряжения возникают за счет неоднородности среды, то через перемещения (мгновенные скорости) можно определить поле деформаций, дилатацию, девиатор (тензор напряжений) и таким образом решать задачи прочности. В будущем данная система уравнений будет апробирована на этих задачах.
Математическая модель тепломассопереноса в пористых и вязких средах
Добавив к полученной системе уравнений вихревой гидродинамики (ВГ) уравнения теплопроводности, массопереноса, уравнение состояния, граничные и начальные условия получим следующую полную сопряженную систему уравнений тепломассопереноса в пористых и вязких средах.
Эта модель в терминах функции тока, давления, температуры и концентрации выглядит так (рис. 3):

Рис. 3. Система уравнений вихревой гидродинамики ВГ (пояснения в тексте)
Здесь Ψ 1,2,3 – проекция вектора функции тока на координатные оси; T – температура; U – потенциальная функция; Ci – концентрация i-го компонента в системе, i =1, m, m – количе- ство компонент; t – время; x, y, z – координаты, Vx,Vy,Vz,Wx,Wy,Wz,аx,ay,az,Ax,Ay,Az,Dx,Dy,Dz,α x,αy,αz, – проекции векторов скоростей конвекции (фильтрации) и тепловой волны, коэффициентов текучести (фильтрации), гидро- динамического сопротивления, гидродисперсии, температуропроводности на координатные оси; в, в, в, Р0, Рф — термический и концентрационный коэффициенты объемного расширения, коэффициент сжимаемости, исходная и текущая плотность среды (флюида); T0,C0,U0,T,C,U – фоновые и текущие температура, концентрация, и потенциальная функция (давление – P или напор – H); D – обобщенный коэффициент дисперсии (диффузии), или коэффициент гидродисперсии. F – обобщенная функция кинетики, превращения веществ. f (t, x, y,z) – функция источников или генераторов, формирующих внешние (сторонние) поля, например транзитный поток или внутренние поля, сформированные в предыдущие моменты времени i=1^5.
В уравнение (11) для задач с пористыми средами используется обобщенный коэффициент дисперсии, или коэффициент гидродисперсии D = DM + DK, где DM - коэф- фициент молекулярной диффузии, D – коэффициент диффузии или механической дисперсии:
D k = A V' , V = V/ X , (14)
V ' – вектор действительной скорости фильтрации, A - параметр механической дисперсии, X - пористость. Для вектора скорости тепловой волны можно записать следующее выражение:
W = V C ф , C п ,
где V – вектор скорости фильтрации, C , C – объемная теплоемкость флюида и флюидонасыщенных пород.
F – обобщенная функция кинетики превра- щения веществ.
др
F i = O k + S i + N i . (16)
д t
Здесь: aik - стехиометрический коэффициент для i-го элемента в k-ой реакции осаждения-Р растворения минералов. – прибыль или д t убыль j-го минерала за счет реакций растворения – осаждения, замещения.
р = ±fl( кk п p5s п CA - п р^ п cA , (17) д t ^ s 1 r q где Сq – моляpная концентpация элементов в поровом водном растворе в моль/л, q = 1^m
Pj - молярная плотность минералов в единице объема в моль/дц3, j=1^ n, Kk - константа равновесия k-й реакции растворения, осаждения r,s-го минералов s,re [1,...j], 5 -стехиометрический коэффициент для s-го или r-го минерала в к-ой реакции. 1 < s,r < n, A - стехиометрический коэффициент l-го или q-го элемента раствора в к-й реакции. 1 < l,q < m Si - прибыль или убыль i-го элемента в растворе за счет равновесных и обменных реакций, i = 1^ m.
к г п cA - rrll s,=±Y
п сЧ , (18)
q J
где K r – константа равновесия r -ой реакции диссоциации или растворения осаждения i-го вещества. A rl - стехиометрический коэффициент для l-го или q -го элемента в r -ой реакции:
1 < l, q < m ,
N i – прибыль-убыль i- го элемента за счет сорбции-десорбции или радиоактивного распада:
N i = a i C i , (19)
где a i - коэффициент сорбции-десорбции при бесконечной емкости, или радиоактивного распада i-го элемента. С i – текущая концентрация i-го элемента.
Количество твердого вещества так же, как и растворенного, рассчитывается в моль/дц3. Пористость X в точке определяется по формуле
X = 1 -S P j Q j , (20)
j где Qj – мольный объем j-го минерала дм3/моль, р - молярная плотность j-го минерала моль/дм3.
Пористость учитывается при образовании твердых осадков реакций, осаждение минералов прекращается, если пористость достигает заданного минимума, и при расчете коэффициента дисперсии на каждом новом временном шаге. Расчет уравнений химической кинетики, записанный на основе закона действующих масс, проводится итерационным методом с использованием случайных чисел. Для решения выписанной системы уравнений задаются граничные и начальные условия:
Т| г =Ф ; Т ( x , y , z ) t = о = F i ( x , У , z ) ;
T\ г = G ; T ( x , y , z ) t = 0 = F 2 ( x , У , z ) ;
С| г = R ; C ( x, y, z ) t = о = F 3 ( x, y , z ) ;
P| г =H ; P ( x, y , z ) t = 0 = F 4 ( x, y, z ) , (21) где, Ф , G, R, H, F i-4 - известные функции.
Это система уравнений шестого и более порядка, в зависимости от количества компонентов (m). Первые четыре уравнения (6, 7, 8, 9) описывают гидродинамику, причем первые три записанные через функцию тока – свободную конвекцию, вызываемую внутренними силами (градиентом плотности), а четвертое, записанное через скалярный потенциал, – вынужденную конвекцию, вызываемую любыми внешними силами. Пятое уравнение – теплопроводности (10), шестое – массопере-носа (11). Прямая связь между гидродинамическим блоком и уравнениями тепломассопе-реноса осуществляется через скорости конвекции (фильтрации) уравнение (12) – обратная через плотность среды (флюида) уравнение состояния (13). Для решения данной системы задаются начальные и граничные условия (21). Любые начальные состояния и внешние воздействия (транзитные потоки и т.д.) или взаимодействия разных веществ между собой и их фазовые переходы задаются с помощью функций источников, записанных в правой части для каждого уравнения (14–20).
Представленная модель эллиптическо-параболического типа, является классической системой уравнений, для численного решения которой подходят большинство разработанных и используемых расчетных методов и схем. Повышенный порядок системы уравнений практически не влияет на методику и технологию разработки программного кода. Это позволило автору на основе экономичных конечно-разностных схем, основанных на расщеплении уравнений по координатам осям и физическим процессам, используя абсолютно устойчивый локально-одномерный метод решения [11], разработать пакет программ на языке Fortran, с помощью которого можно решать широкий круг трехмерных задач теп-ломассопереноса в пористых и вязких средах на персональных компьютерах.
При решении задач используются три безразмерных комплекса. Первые два это тепловое и концентрационное числа Фурье Fot = ат/L2, Foc = Dt/ L2. В уравнениях, описывающих свободную и вынужденную конвекцию, возникающую за счет градиента плотности среды (флюида) или внешних сил, коэффициент пропорциональности k2 = (g/p)x(p/L) = g/νL определяет плотность потока линий тока, характеризующий его интенсивность, в общем случае является тензором второго ранга и имеет размерность 1/(м2сек). Физический смысл этого коэффициента можно интерпретировать как текучесть, а его обратное значение k1 = 1/k2, – как гидродинамическое сопротивление (чем больше сопротивление среды, тем больше плотность источников). Поэтому третий безразмерный комплекс можно назвать критерием плотности распределения линий тока вихревой гидродинамики (ВГ), Плт = (g/p)x(p/L)xL2T. В уравнениях этих трех комплексов a, D, p,v, g - коэффициенты температуропроводности, диффузии, динамической и кинематической вязкости, ускорения свободного падения, т, L2, L - характерное время, площадь и размер в решаемой задаче.
Основную нагрузку при интерпретации огромного объема результатов вычислений несет пакет графических программ визуализации, разработанный автором и позволяющий в динамике просматривать значения любой функции, вычисленной при решении поставленной задачи.
Численная реализация
Для решения системы уравнений, описывающей процессы конвективного тепло-массопереноса в трехмерных областях, необходимо использовать численные методы, позволяющие в каждом узле дискретной сетки, покрывающей модельную область, рассчитать значения искомых функций. Для численной реализации краевых задач используется абсолютно устойчивый локально-одномерный метод решения [11]. Суть его заключается в расщеплении уравнения по координатам и последующем решении одномерных уравнений методом прогонки, в сумме являющихся решением многомерного уравнения. Эта неявная схема решения имеет суммарную аппроксимацию порядка о(г + h 2 ) , где т - шаг по времени, h - шаг сетки. Для аппроксимации конвективных членов в уравнениях (10, 11) используется схема с направленными разностями [12]. Кроме того, эти уравнения расщепляются по процессам, т. е. в каждый момент времени вначале учитывается вклад только кондуктивного и дисперсионного членов, рассчитанных по неявной схеме, а затем к ним добавляются значения конвективных составляющих, рассчитанных по явной схеме.
При решении уравнений Пуассона (6–9) применяется метод установления с нижней релаксацией [10]. Процесс считается установившимся при условии
S ^ £ Т m , (22)
где S – максимальное по всем узлам сетки значение невязки, Ти - максимальное по модулю значение функции тока или потенциала, £ = 0,01 - 0,001. Количество итераций для установления процесса зависит от шага по времени и параметров среды. При малом шаге по времени Т и/или однородной структуре среды процесс устанавливается за 1–2 итерации, при большем шаге Т и/или неоднородной структуре среды или при относительно больших коэффициентах проницаемости (текучести) в начальные моменты времени итераций требуется больше, но затем количество итераций быстро уменьшается и стабилизируется в пределах 3–5.
Схему решения краевой задачи на каждом шаге по времени можно представить в следующем порядке:
-
1. По распределению температуры Tn - 1, концентрации Cns - 1 и если есть источники, функции Un-1, согласно уравнению (13), определяется плотность - p n .
-
2. По уравнениям (6–8) рассчитываются функции тока Т n при известной правой части.
-
3. Определяется распределение потенци
-
4. По функциям тока и потенциалу вычисляются скорости конвекции (фильтрации) Vn , Vn , Vn . Для пористых сред по скоростям фильтрации вычисляются скорости тепловой волны W n , W n , W n , коэффициенты гидродинамической дисперсии Dnx , Dny , Dnz и действительные скорости фильтрации V' n , V ' У , V ' n .
-
5. Используя скорости конвекции или тепловой волны (для пористых сред), определяется температура T n .
-
6. Используя скорости конвекции и диффузии или коэффициенты гидродинамической дисперсии и действительные скорости фильтрации (для пористых сред), определяется концентрация растворенных веществ C n .
-
7. Если в системе учитывается кинетика превращения веществ или взаимодействия вода-порода, сорбция-десорбция (для пористых сред), то рассчитывается функция источника для уравнения (11).
альной функции Un, при наличии не нулевых граничных условий или источников по уравнению (9).
Этот цикл повторяется для всех последующих моментов времени с использованием результатов решения уравнений Пуассона как начальных условий с предыдущего временного слоя.
Начальные и граничные условия
Для скалярных функций T,C,U – задаются стандартные начальные условия, значения функций в точке. Для проекций функции тока задаются нулевые начальные условия Т 1А3 1 0 = 0, или, если существует транзитный поток, вызванный какими-то внешними силами, значения для любой из этих функций – в виде числовой последовательности с заданным шагом для формирования потока с определённой скоростью в рассматриваемой области, например, горизонтальный поток вдоль координаты х, Т 1 1 0 = KxAxxN, где К - коэффициент пропорциональности, Δx – шаг по координате x, N – количество точек разбиения. Граничные условия первого, второго, третьего или четвертого рода задаются для скалярных функций, хотя при выносе границ за пределы области влияния процессов их можно свести к условиям первого и второго рода. Для скоростей на гранях расчетной области используются условия, записанные через проекции функции тока. Для условий не-протекания и проскальзывания т| г = 0. Для нормальных скоростей условие протекания, а для касательных (тангенциальных) скоростей условие прилипания дТ / д п | г = 0.
Условия применения
Модель реализована в виде пакета программ на языке Fortran для ПК типа IBM. Трансляция проводится с помощью компилятора Fortran PowerStation, позволяющего получать оптимизированные 32-разрядные приложения, работающие в операционных системах DOS и Windows.
Время расчета задачи определяется количеством точек в расчетной области и количеством моментов времени, на которое ведется расчет. Так, для области, разбитой сеткой на 45000 точек (50x30x30), при решении задачи в пористых средах на 7300 моментов времени (что составляет 20 лет, если шаг по времени – 1 сутки) время счета на AMD-2000 составляло 150 минут (2,5 часа). При использовании кинетики взаимодействия вода-порода время расчета резко возрастает и намного увеличивается объем результатов вычислений.
В задачах с высоковязкими средами, для области разбитой сеткой на 72000 точек (45 x 40 x 40) и с корректировкой вязкости в зависимости от температуры и концентрации среды, при расчете на 16000 моментов времени с шагом 100 – 1000 лет требуется 90 минут (1,5 часа) расчетного времени на персональном компьютере Pentium G620-2.6GHz. Это вполне приемлемо для задач такого класса. При увеличении или уменьшении количества точек или моментов времени время счета пропорционально увеличивается или уменьшается.
Результаты расчета по каждой функции и заданного момента времени выводятся в файлы прямого доступа, затем просматриваются с помощью графических программ, разработанных автором, позволяющих наблюдать изменение вычисленных функций в динамике. При каждом расчете в файл прямого доступа выводятся 20–30 срезов по времени для каждой функции, что в сумме составляет 75–150 Mb дисковой памяти. Тоновые рисунки результатов расчетов представлены в виде блок-диаграмм и (или) горизонтальных срезов по вертикальной координате, вертикальных по горизонтальным для определенного момента времени. Разметка координат – в метрах или километрах. Стрелками показано поле скоростей фильтрации (конвекции) в пяти диапазонах, выделенных цветом. Для каждого диапазона написано максимальное значение скорости, соответствующее максимальной длине стрелки на рисунке.
Распределение концентрации веществ и температуры показано оттенками синего и красно-желтого цвета, с указанием абсолютного максимума. В текстовый файл для контроля выводятся исходные данные и значения рассчитанных функций для первого, промежуточного, и последнего моментов времени в виде двумерных матриц-срезов по одной из координат.
Анализ результатов
С использованием системы уравнений (ВГ), был решен и опубликован в Российских и зарубежных изданиях ряд задач для пористых, высоковязких и низковязких сред, результаты некоторых из них проанализированы в данной работе.
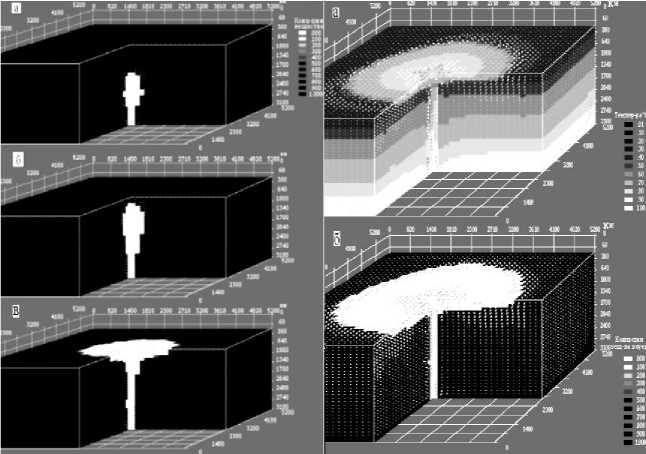
Рис. 4. Слева – динамика подъема плюма на три момента времени с распределением концентрации вещества среды (белым цветом выделен расплав) и поля скоростей конвекции (максимальная скорость стрелки желтого цвета): а) через 24 млн лет, V max = 0,28 м/год; б) через 32 млн лет, V max = 0,42 м/год; с) через 48 млн лет, V max = 0,8 м/год, после начала подъема плюма. Верхняя часть блоков срезана по подошве литосферы. Справа – распределение: а) температуры Тmin = 200°С, Тmax = 3100°С, и поля скоростей конвекции Vmax = 0,8 м/год (желтый цвет стрелок); б) концентрации вещества среды (белым цветом выделен расплав), в линзе расплава у подошвы литосферы через 100 млн лет
Для высоковязких сред анализировались задачи по оценке условий формирования и эволюции нижнемантийного плюма (рис. 4) и условий формирования и развития диапиров в системе литосфера – кора (рис. 5) [4, 5, 6].
Для пористой среды задачи о становлении интрузива как одного из механизмов формирования условий для образования кольцевых и вихревых структур [3] (рис. 6).
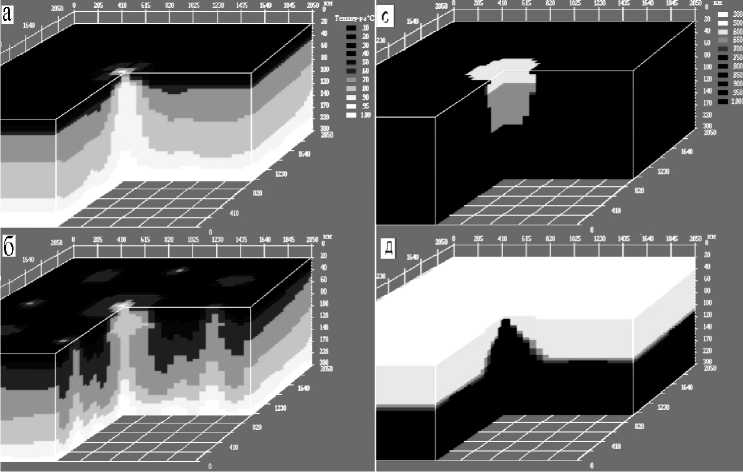
Рис 5. Распределение температуры при различной вязкости окружающих пород и плотности вещества диапира при относительно высокой его вязкости (1–3 порядка ниже вязкости окружающих пород) после подъема диапира; а) вязкость окружающих пород равна 1022 П - с, Tmax = 1730°С; б) вязкость окружающих пород в десять раз меньше, Tmax = 1690 °С; с) вещество диапира претерпевало фазовые переходы; д) вещество диапира не претерпевало фазовые переходы
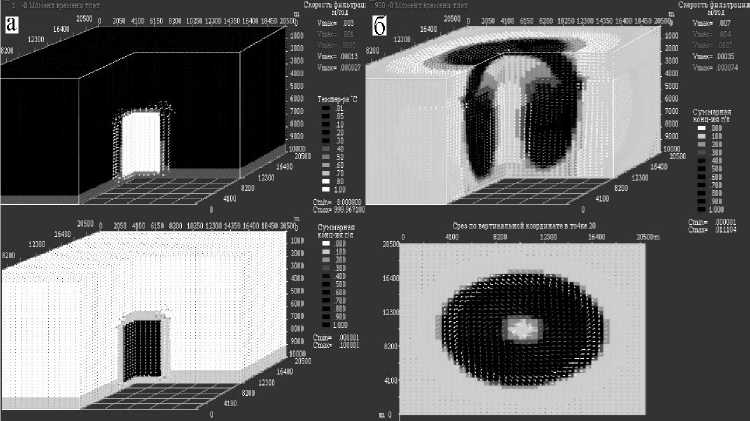
Рис 6. Схематичный блоковый разрез области расчета: а) распределение температуры Ттах = 1000 °C, Т m in = 5 ° C концентрации вещества и поля скоростей фильтрации флюида Vmax = 0,003 м/год в начальный момент времени после внедрения интрузива в пористую среду верхней коры; б) распределение вынесенного потоком флюида из интрузива вещества и поле скоростей фильтрации через 200 000 лет, срез сделан на глубине 5 000м, V max = 0,007 м/год
Для низковязкой среды (гидросферы) рассмотрены задачи по оценке причин и условий формирования кольцевых структур на льду и газовых выбросов в летний период из озера Байкал. [7, 8] (рис. 7).
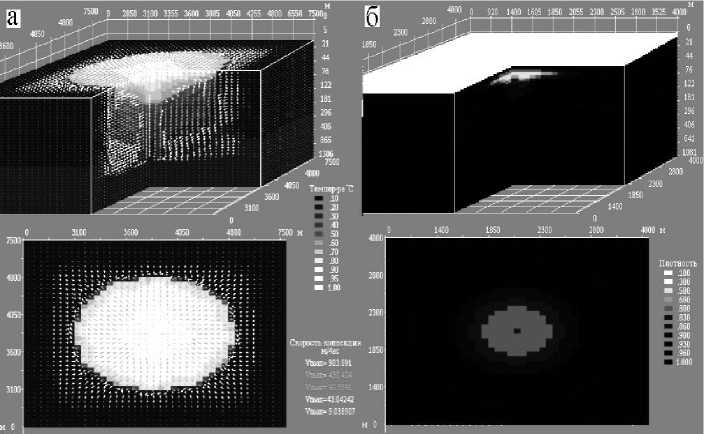
Рис 7. Формирование кольцевых структур на льду озера Байкал: а) распределение температуры и поля скоростей конвекции при образовании линзы у подошвы ледяного покрова; б) распределение плотности воды при формировании кольцевой структуры подо льдом озера Байкал (лед отрисован белым цветом)
В этих задачах моделировалось влияние источника тепла и/или химического вещества, снижающих плотность мантийного (плюм) и литосферо-корового (диапир) материала для сплошной среды, или флюидов для пористой среды. Для гидросферы задавался источник с повышенной температурой или пониженной плотностью (газ).
Во всех случаях шел одинаковый процесс формирования восходящего и нисходящего потоков (струй), который состоял из нескольких этапов развития. Над заданным источником появлялась куполообразная структура с пониженной плотностью и вязкостью.
Для каждого координатного направления формировался гидродинамический диполь и стратификация становилась неустойчивой (неустойчивость Рэлея–Тейлора). За счет горизонтального градиента плотности возникали выталкивающие силы (силы Архимеда) и куполообразная структура всплывала, формируя восходящий конвективный поток торообразного вида с восходящей ветвью в центре структуры (канале) и нисходящей в окружающем массиве (среде).
При больших размерах источника и бо- лее низкой вязкости среды возможно образование мульти-диполя и появление нескольких симметрично расположенных куполообразных структур (рис. 5,б). Скорость подъема потока зависела от его плавучести и вязкости для сплошной среды и проницаемости среды и вязкости флюида для пористой. За счет вертикального градиента плотности появлялись тангенциальные силы, вызывающие вращение структуры.
В центральной и головной частях поток вращался против часовой стрелки (циклонический вихрь), а на периферии, где шло погружение, и в подошве структуры -по часовой стрелке (антициклонический вихрь) (рис. 8).
При достижении потоком более вязкой среды (преграды) подъем его прекращался, вещество потока растекалось по его подошве, формируя линзу с вращением в центральной ее части против часовой стрелки, а на периферии - по часовой стрелке. Если преграда отсутствовала, то поток мог внедриться в менее плотную среду (гидросферу, атмосферу) и сформировать кольцеобразную структуру (рис. 6,б, 7,б).

Рис. 8. Распределение плотности среды и поля скоростей при подъеме конвективного потока (струи) для трех моментов времени развития процесса. В верхней и нижней областях рисунка показаны горизонтальные срезы в головной (для каждого) и подошвенной (для всех) моментов времени подъема струи. Максимальная скорость потока - желтый малиновый цвет в центре струи, минимальная - белый цвет на периферии
Анализ системы уравнений и результатов, полученных при решении этих задач, позволил сделать некоторые обобщения по причинам и следствиям динамики процессов, развивающихся в различных геосистемах.
Выводы
На основе этого анализа и ранее опубликованных материалов можно сделать следующие выводы. Всеми процессами и явлениями в нашем мире управляет гравитация. Это основной источник движения и преобразования вещества в природе. Гравитационное поле имеет не только скалярный потенциал (нормальную составляющую), но и векторный (вихревую составляющую) rot A ≠ 0, а генератором вихрей является ∇ρ – градиент плотности. Вертикальный градиент плотности вызывает тангенциальные силы, приводящие различные среды к вращению в горизонтальной плоскости, а горизонтальный градиент плотности вызывает их вертикальные движения (подъем, погружение). Это новое фундаментальное свойство гравитационного поля.
Причиной появления (действия) силы Кориолиса является не вращение Земли, а тангенциальная составляющая гравитационного поля. Это можно подтвердить с помощью простого примера. В ясную морозную погоду, когда влажность воздуха минимальна, а значит его плотность максимальная, дым, поднимаясь из печной трубы, буквально вкручивается в воздух. Если на следующий день, при повышении температуры, а значит и влажности воздуха, плотности их становятся близкими, то дым стелется по земле, успевая только чуть подняться над трубой. Это говорит о том, что причиной такого поведения дыма является разность плотности дыма и воздуха, чем она больше, тем с большей скоростью и выше поднимается дым из трубы (рис. 9).

Рис. 9. Подъем дыма из печной трубы: а) - ясная морозная погода, влажность воздуха минимальна, его плотность максимальная р д<< р в ; б) - при повышение температуры, а значит и влажности воздуха, плотности их близки р д ~ р в
Во всех пограничных слоях разных сред (оболочек Земли) существует скачок плотности, который активизирует (генерирует) тангенциальные силы гравитационного поля, а те в свою очередь формируют вихревые потоки. Менее плотные верхние слои плывут по нижним слоям с вращением по часовой стрелке, формируя ан-тициклонический вихрь. Движение этих потоков осложняется рельефом нижнего, более плотного, слоя. Такие потоки – придонные (приповерхностные) течения – существуют в атмосфере, реках, озерах, морях и океанах.
За счет этих же сил верхняя твердая оболочка Земли (литосфера) разбита на плиты, а те в свою очередь – на более мелкие блоки верхней более твердой коры. Все эти плиты и блоки движутся относительно друг друга, вращаясь на более плотном основании и/или перемещаясь в вертикальном направлении, при подъеме формируя материки, а при погружении – озера, моря и океаны. Так как эти плиты и блоки плотно упакованы, то никаких горизонтальных перемещений у них быть не может, к тому же материки, моря и океаны являются тонкой пленкой на поверхности литосферных плит и составляют 1,5–2 % от ее мощности-толщины. Иллюзию же перемещения создает движение в виде погружения одного и подъема другого с обоюдным вращением двух соседних блоков (рис. 10).

Рис. 10. Современные сейсмичность, вулканизм и границы плит: материк и океан могут располагаться на одной плите. Желтые точки - очаги землетрясений, красные треугольники - активные наземные вулканы
В северном полушарии Земли большая часть коры испытывает вздымание (подъем) с вращением против часовой стрелки (циклонический вихрь) поэтому основная часть материков находится в этом полушарии. В южном полушарии большая часть коры погружа- ется с вращением по часовой стрелке (анти-циклонический вихрь) и покрыта океанами. Результирующая тангенциальная сила направлена с запада на восток, она приводит планету к вращению в том же направлении, т.е. с запада на восток (рис. 11).

Рис. 11. Распределение материков и океанов на поверхности планеты Земля. Слева геоид - уровневая поверхность потенциала силы тяжести, имеет форму груши вытянутой к северному полюсу, желтый цвет - максимальная гравитация, синий - минимальная. Справа - глобус
Более того, собственные колебания (их еще называют свободные ) всех тел и объектов на нашей планете являются результатом действия вихревой составляющей гравитационного поля, так как между поверхностью опоры, на которую они опираются или к которой крепятся, существует градиент плотности, приводящий к вращающему моменту, возбуждающего колебания. Поэтому собственные колебания тел, объектов и систем – результат действия тангенциальных сил гравитационного поля.
Все процессы, проходящие в глубинах Земли и на ее поверхности, одинаковы по физической сути, но имеют различные временные масштабы от секунд до нескольких суток на ее поверхности и до десятков и сотен миллионов лет в ее глубинах. Это позволяет результаты, полученные при изучении более доступных процессов на поверхности Земли, применять для изучения и понимания менее доступных глубинных процессов. Полагаем, такой универсальный подход может послужить дополнительным импульсом для развития наук о Земле.
Список литературы Вихревая гидродинамика: новый подход к моделированию геосистем
- Гебхарт Б., Джалурия Й., Махаджан Р., Саммакия Б. Свободноконвективные течения, тепло- и массообмен: в 2 кн. / пер. с англ. М.: Мир, 1991. С. 678.
- Глуховский М.В. Кольцевые структуры юго-востока Сибири и их возможная природа // Геотектоника. 1978. № 4. С. 50-63.
- Гунин В.И. Становление интрузива как возможный механизм формирования условий для образования кольцевых и вихревых структур (численный эксперимент) // Известия вузов. Геология и разведка. 2006. № 4. С. 40-44.
- Гунин В.И. Оценка условий формирования и эволюции нижнемантийного плюма на основе численного эксперимента // Геодинамика формирования подвижных поясов земли: матер. Междунар. науч. конф. Екатеринбург, 24-26 апреля 2007. С 75-78.
- Гунин В.И. Оценка условий формирования-развития диапиров в литосфере и земной коре на основе численного эксперимента // Граниты и эволюция Земли: I Междунар. конф. Улан-Удэ, 26-29 августа 2008. С. 97-101.
- Гунин В.И. Новая информационная технология и ее возможности при моделировании геосистем // Геодинамика и тектонофизика. 2011. Т. 2, № 4. С. 356-377. URL: http://gt.crust.irk.ru (дата обращения: 12.11.2017).
- Гунин В.И. Оценка причин и условий формирования кольцевых структур на льду Байкала по результатам численного эксперимента // Подземная гидросфера: матер. Всерос. совещания по подземным водам востока России. Иркутск: Изд-во ООО "Географ", 2012. С. 513-517.
- Гунин В.И. Оценка воздействия газогидротермальной деятельности Байкальского рифта на акваторию озера по результатам численного эксперимента // Геодинамика и тектонофизика. 2014. Т. 5, № 3. С. 763-775. URL: http://gt.crust.irk.ru (дата обращения: 20.11.2017).
- Кирюхин А.В., Сугробов В.М. Модели теп-лопереноса в гидротермальных системах Камчатки. М.: Наука, 1987. 150 с.
- Тарунин Е.Л. Численный эксперимент в задачах свободной конвекции, Иркутск: Изд-во Иркут. ун-та, 1990. 223 с. (41).
- Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1975. 735 с.
- Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. 429 с.


