Визуализация и анализ профиля обращений в память
Бесплатный доступ
Для большинства задач из любой предметной области для получения их эффективной реализации необходимо проводить анализ работы с памятью. В данной работе проводится исследование профиля доступа к памяти на примере некоторых типовых задач. На основе данного исследования с помощью визуализации проводится анализ возможных свойств рассмотренных задач, а также выделяются некоторые общие закономерности. Приводятся примеры визуализации профилей работы с памятью, иллюстрирующие указанные свойства и особенности.
Исследование эффективности, типовые алгоритмические структуры, профиль обращений в память, характеристики работы с памятью, визуализация профиля
Короткий адрес: https://sciup.org/147159091
IDR: 147159091 | УДК: 519.683
Текст научной статьи Визуализация и анализ профиля обращений в память
Для многих задач эффективность выполнения программ является очень важным фактором. Чем выше эффективность выбранного решения, тем быстрее программа будет выполнена, тем меньше времени будет потрачено на решение задачи в целом. В области суперкомпьютерных вычислений многие задачи требуют часы, дни, а иногда и недели для решения, поэтому даже незначительное увеличение эффективности может привести к существенному выигрышу в скорости работы программы.
Для повышения эффективности программ на сегодня разработано множество различных средств, однако они всегда нацелены на относительно узкую область: либо на определенный класс вычислительных платформ, либо на предопределенный класс задач, либо на оптимизацию конкретных свойств программ. Для решения проблем общего характера, например, подбора наиболее эффективной платформы для выбранной задачи или эффективной реализации задачи на другой платформе, данные средства плохо подходят. Нужен более общий подход, позволяющий проводить исследование эффективности всего процесса отображения задач на архитектуру вычислительных систем.
Для изучения процесса отображения предлагается на каждом из его этапов выделять набор характеристик, которые могут влиять на эффективность или же помогать в ее исследовании [1, 2]. Все характеристики делятся на три класса: характеристики алгоритма, программы и аппаратуры. Предполагается, что во время отображения задачи и алгоритм, и платформа уже определены, поэтому их характеристики фиксированы. По сути, эти характеристики описывают те рамки, в которых программа должна работать. Для получения эффективной реализации мы можем менять характеристики программы в соответствии с характеристиками алгоритма и аппаратуры. Примерами указанных характеристик из различных классов могут служить следующие параметры:
-
• Характеристики алгоритма: свойства графа алгоритма [3];
-
• Характеристики программы: свойства текста программы (структура вхождения циклов, способ индексации массивов и т.д.), коммуникационные свойства (объем передаваемых данных, структура передач, число нитей/процессов);
-
• Характеристики аппаратуры: строение подсистемы памяти, топология, латентность и пропускная способность сети.
Одним из самых главных факторов, влияющих на эффективность выполнения программы, является эффективность работы с памятью. Эта проблема известна и получила название «стены памяти»: все последние годы скорость работы процессоров растет значительно быстрее скорости работы памяти. Во всех современных вычислительных системах доступ к данным является дорогостоящей операцией, поэтому неэффективное использование памяти может очень сильно сказываться на производительности всей выполняемой программы. Вместе с этим, подсистема памяти устроена очень сложно, и ее оптимальное использование является непростой задачей. Кэш-памяти разных уровней, оперативная память, TLB буфер, аппаратный префетчер — каждый из этих компонентов подсистемы памяти обладает целым набором аппаратных характеристик, которые необходимо учитывать для эффективной работы с памятью.
На данный момент разработаны различные программные средства и проводятся исследования, направленные на анализ и повышение эффективности работы с памятью, например, с помощью сбора информации об эффективности использования кэш-памяти [4] или эмуляции работы программы [5]. В данной работе акцент делается на визуальном анализе структуры доступа к памяти, который во многих случаях дает интересную информацию о свойствах программы, и главное — об эффективности ее выполнения. Стоит отметить, что активно визуализация используется и при исследовании других свойств программ, например, коммуникационного профиля параллельных программ [6].
1. Профиль работы с памятью и характеристики программ
Для исследования и анализа эффективности программ важно понимать структуру их профиля работы с памятью. Введем понятие «поток обращений», под которым будем понимать последовательность обращений к используемым в программе переменным, записанную в том порядке, как это происходило при выполнении программы. Если задействован элемент массива или другой составной переменной, то в поток попадает именно этот элемент, а не вся составная переменная. Таким образом, в поток обращений могут входить скалярные переменные, составные переменные (если в некоторой операции адресуется такая переменная целиком) или отдельные элементы составных переменных. Если для работы с элементами составной переменной используется некоторый итератор, то для каждого конкретного значения итератора в поток обращений записывается отдельное обращение. В случае итерирования массива в потоке обращений появятся отдельные элементы данного массива. Например, если в программе есть код:
for (i=0; i<4; i++) A[i]=0;
то поток обращений к массиву А будет выглядеть следующим образом: А[0], А[1], А[2], А[3].
Для изучения профиля работы программ с памятью можно опираться на различные подходы. Один из возможных вариантов — это использование специальных характеристик программы, описывающих локальность используемых данных. В работе [2] для описания пространственной и временной локальности данных программы вводится набор характеристик. Первые две характеристики описывают пространственную локальность, которая отражает среднее расстояние между несколькими последовательными обращениями к памяти. Характеристика L показывает среднее расстояние по памяти между всеми соседними элементами потока обращений. Это дает оценку, насколько близко в памяти расположен следующий элемент данных по отношению к текущему. Характеристика SEQ_L отражает среднюю длину последовательных элементов потока, являющихся непосредственными соседями в памяти. Данная характеристика позволяет оценить самый хороший случай для пространственной локальности, когда используемые данные следуют в памяти подряд, что дает хорошее использование кэш-памяти.
Для описания свойств временной локальности выделяются три характеристики. Временная локальность данных программы показывает среднее число обращений по одному адресу в памяти за время исполнения всей программы. Характеристика Alpha равна среднему расстоянию (в терминах потока обращений) до следующего обращения к той же переменной, что показывает интенсивность использования данных. Степень влияния этой характеристики, а также отдельных переменных на эффективность работы программы в целом, позволяет оценить характеристика N_Alpha, которая равна среднему числу обращений к переменным (элементам потока). Чем больше обращений произведено к некоторой переменной, тем важнее с точки зрения эффективности работы с памятью интенсивность обращений к данной переменной. Степень повторного использования переменных программы показывает характеристика Р, значение которой изменяется на отрезке [0, 1]. Характеристика Р принимает крайние значения в следующих случаях: если ко всем переменным программы обращение происходит только один раз, то Р=0, а если ко всем переменным обращение происходит как минимум дважды, то Р=1.
Более подробное описание и примеры использования данных характеристик приведены в работе [2].
2. Визуализация профиля работы с памятью
Для изучения качественных характеристик профиля работы программ с памятью хорошие результаты дает его визуализация. Конечно, визуализация не дает возможности получить точные оценки или провести аккуратный детальный анализ, однако она позволяет понять общее строение профиля, как в целом устроена программа, что во многих случаях может дать подсказку пользователю о дальнейших действиях.
В данной работе мы будем рассматривать профили работы с памятью для некоторых типовых алгоритмических структур [1, 2]. Для каждого массива строятся отдельные профили. Все профили на рисунках устроены одинаково: по вертикали расположены линеаризованные индексы элементов массива (т.е. смещение элемента относительно начала массива), по горизонтали — номер обращения в потоке (чем больше этот номер, тем позже было произведено данное обращение в программе).
Стоит сразу отметить, что картинка никак не отражает время, затрачиваемое на обращение к различным компонентам подсистемы памяти (например, кэш-памяти или ОН), которое может сильно отличаться для разных обращений. Данное представление является машинно-независимым, и не всегда позволяет сделать точные выводы о работе реальной программы.
Также, поскольку число обращений в потоке часто весьма велико, то визуализация всего профиля может быть обманчива, и для точного анализа, вообще говоря, необходимо рассматривать отдельные, небольшие фрагменты профиля. Возьмем, например, профиль работы с памятью для вектора в задаче умножения разреженной матрицы на плотный вектор (рис. 1а). На первый взгляд, кажется, что данный профиль отражает полностью случайный характер обращения к элементам вектора, однако при увеличении масштаба видно, что обращения к вектору имеют закономерность (рис. 16).
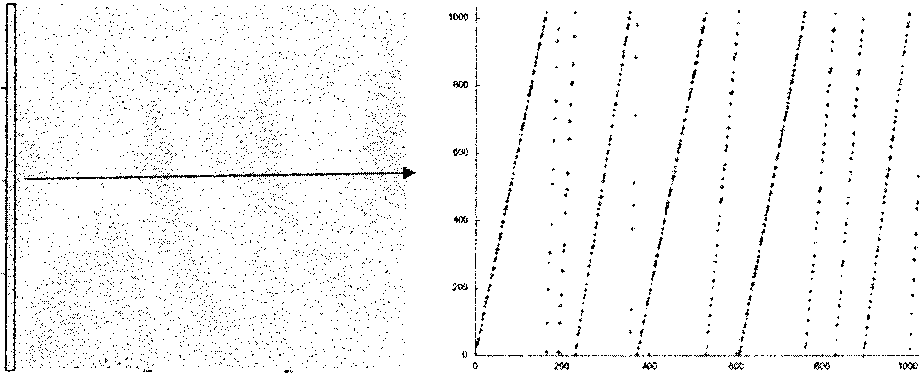
а) б)
Рис. 1. а) общий профиль, более 100,000 обращений в память; б) увеличенный фрагмент, 1024 обращения в память
Несмотря на то, что при рассмотрении общего профиля точный анализ недоступен, некоторые выводы касательно работы с памятью все же можно делать. Например, график на рис. 2а позволяет предположить, что для любого элемента массива все обращения к нему расположены близко друг к другу, и при этом элементы массива перебираются последовательно, значит, массив обладает достаточно хорошей пространственной локальностью. На рис. 26 видно, что правая часть профиля портит общую локальность, поскольку обращения происходят ко всем элементам массива, причем порядок обращений похож на случайный. Вместе с этим, число обращений в этой правой части значительно меньше, чем во всей остальной части, поэтому его влияние на общий профиль будет не так велико.
Рассмотрим более интересный пример — блочное перемножение плотных квадратных матриц (N — размерность матриц, BLOCK — размер блока):
for(il=0; iKN; il+=BLOCK)
for (j 1=0; jKN; jl+=BLOGK)
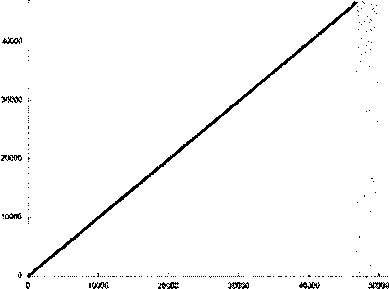
for(kl=0; kl for (i=il; i for (j=jl; j for(k=kl; k } а) б) Рис. 2. а) пример профиля с хорошей пространственной локальностью; б) измененный профиль, пространственная локальность ухудшается В случае при N=128, BLOCK=16 профили работы с памятью для массивов А, В и С выглядят следующим образом (рис. За,36,Зв). а) б) в) Рис. 3. а) профиль обращений в память к массиву А; б) профиль обращений в память к массиву В; в) профиль обращений в память к массиву С В данном случае индекс из двумерного линеаризуется в одномерный, с учетом того, что матрица хранится по строкам. По вертикали, как обычно, указан индекс элемента массива, к которому происходит обращение, а по горизонтали — порядковый номер обращения. Данные графики показывают, что профили массивов А и С похожи — элементы массивов образуют 8 (128/16) блоков, и сначала происходят обращения только к первому блоку, затем — только ко второму и т.д. Это указывает на хорошую локальность обращений, поскольку все обращения к каждому элементу расположены близко друг к другу. В случае массива В ситуация иная: из профиля на рис.Зб видно, что каждый элемент используется на протяжении всей программы и через большие промежутки времени, а значит, локальность в этом случае, скорее всего, хуже, чем в случае массивов А и С. Рассмотрим для более точного анализа небольшие участки профиля. Более подробное изучение профилей массивов А и С на рис. 4а и рис. 46 позволяет заметить, что локальность данных лучше в случае массива С. а) б) Рис. 4. а) профиль обращений к массиву А при выполнении двух внутренних циклов; б) профиль обращений к массиву С при выполнении двух внутренних циклов Сравнивая профили на данных рисунках, полученных при выполнения двух внутренних циклов фрагмента перемножения матриц, видно, что все обращения к элементу массива С идут подряд, в то время как обращения к элементам массива А происходят с некоторым шагом, что приводит к менее эффективной работе с памятью. Конечно же, все качественные заключения, полученные при изучении профилей работы с памятью, находят отражение и в соответствующих характеристиках программ. Рассмотрим значения описанных выше характеристик локальности использования данных, и сравним полученные результаты (табл. 1). Таблица 1 Значения характеристик для задачи блочного перемножения матриц, N=128, BLOCK=16 Массив L SEQ_L Alpha N_Alpha Р А 0,2706 16,0009 0,0006 128 1 В 0,0041 1 0,00007 128 1 С 0,681 512,438 0,0044 256 1 Сейчас не нужно внимательно анализировать абсолютные значения характеристик. Важно, что для каждой из характеристик верно следующее утверждение: чем больше значение характеристики, тем лучше (выше) локальность обращений к данным программы. Иными словами, выводы, сделанные по профилям на рисунках, подтверждаются значениями характеристик. Следует еще раз подчеркнуть возможную обманчивость первого восприятия всего профиля целиком. С этой точки зрения, изначальное предположение о том, что, согласно рисункам, работа с массивом В организована менее эффективно, чем работа с массивами А и С, могло оказаться и неверным. Например, программа могла быть устроена так, что к элементам массива В происходят последовательные обращения на протяжении многих итераций, в то время, как в каждом блоке обращений к массиву А профиль работы с памятью мог носить случайный характер. В такой ситуации локальность обращений к массиву В оказалась бы лучше, чем к массиву А. Это еще раз подчеркивает, что общая картина профиля не всегда адекватно отражает реальные свойства программы. Нужно отметить и тот факт, что далеко не всегда обращения к памяти имеют «линей-ныйжарактер, как могло показаться из приведенных выше рисунков. Рассмотрим профиль работы с памятью для другой типовой алгоритмической структуры — быстрого преобразования Фурье (рис. 5). Для решения использовался простой нерекурсивный алгоритм. Несмотря Рис. 5. Профиль работы с памятью для задачи БПФ на достаточно сложную структуру обращений к памяти, на данном графике легко можно увидеть 3 этапа алгоритма. На этапе 1 происходит начальное преобразование входного массива для последующего расчета. На этапе 2 выполняются основные вычисления, причем отчетливо видно увеличение шага по элементам массива в 2 раза на каждой последующей итерации. Этап 3 соответствует записи результатов в выходной массив. В заключение рассмотрим еще один интересный пример: умножение разреженной матрицы размером NxN на вектор с диагональной схемой хранения. В такой схеме хранения матрицы i-й диагональю называется совокупность ненулевых элементов, расположенных на i-м слева месте в каждой строке. То есть нулевая диагональ — это совокупность первых в строке ненулевых элементов. В случае, если в строке нет i-ro элемента, в i-й диагонали не будет присутствовать ни одного элемента из данной строки. Данная форма хранения матриц используется в тех случаях, когда нужно работать с длинными векторами, а диагональная схема, в данном смысле, имеет большое преимущество перед популярными столбцовой или строчной формами. Алгоритм выглядит следующим образом: for (j = 0; j <= num_diag-l; j++) for (i = ip[j]; i <= ip[j+l]-l; i++) b[ia[i]J = b[ia[i]]+a[i]*x[ic[i]] ; В массиве а записана матрица по диагоналям (всего в матрице num_diag диагоналей), х — вектор, b — результирующий вектор. Массив ip хранит номера строк, отмечающих начало и конец каждой диагонали, а массивы ic и ia содержат соответственно номера столбцов и строк элементов матрицы. Рассмотрим профиль обращений к вектору х. Данный профиль зависит от того, каким образом формируется разреженная матрица. Для начала рассмотрим такую стратегию выбора ненулевых элементов — для каждой строки случайным образом выбирается число ненулевых элементов в ней. Для каждой строки случайным образом выбирается первый элемент в диапазоне от 0 до N-K-1, где К — число ненулевых элементов в данной строке; затем выбирается второй элемент в диапазоне от А1+1 до N-K-2, где А1 — номер столбца первого ненулевого элемента; и т.д. В результате образуется следующий профиль (рис. 6). Данный профиль позволяет увидеть, что большинство обращений происходит к элементам, Рис. 6. Профиль работы с памятью для задачи умножения разреженной матрицы на вектор, первый вариант заполнения матрицы расположенным в конце массива х. Следовательно, выбранный способ формирования матрицы приводит к тому, что большинство ненулевых элементов скапливается в последних столбцах матрицы. В случае если желательно получить более равномерное распределение ненулевых элементов в матрице, можно использовать другой способ их выбора: разделим строку на К равных частей, и в каждой части случайным образом выберем один элемент. В этом случае обращения к элементам массива х будут более равномерными, что и отражает профиль, показанный на рис. 7. Рис. 7. Профиль работы с памятью для задачи умножения разреженной матрицы на вектор, второй вариант заполнения матрицы Заключение Все профили программ, приведенных в данной работе, построены с помощью простого подхода: сначала фиксируется поток обращений анализируемой программы к памяти, который затем визуализируется с помощью системы gnuplot. Формирование потока обращений делается путем сохранения после каждой операции с массивом индекса задействованного элемента. Безусловно, для детального изучения профиля работы программ с памятью необходим полноценный инструментарий, объединяющий глубокий аналитический анализ с развитыми возможностями по визуализации. Данный инструмент должен позволять выбирать для анализа только необходимые переменные и фрагменты кода, легко управлять объемом собираемых данных, иметь гибкие средства фильтрации, агрегирования, позволять менять масштаб и выбирать область для детального исследования. Разработка подобного инструмента стоит в плане работ на будущее, но все текущие исследования выполняются более простыми средствами. Приведенное исследование показывает, что для обеспечения эффективной работы программ стоит изучать и анализировать профиль работы с памятью. Данный анализ можно проводить различными способами, одним из которых является исследование результатов визуализации профиля. Несмотря на то, что данный способ не позволяет проводить точный анализ, он помогает понять на общем уровне, каким образом происходит работа с памятью в программе, а также сделать некоторые выводы касательно общей эффективности использования памяти. Статья рекомендована к публикации программным комитетом международной научной конференции -^Параллельные вычислительные технологии 2011>.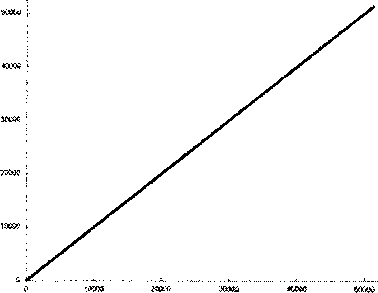
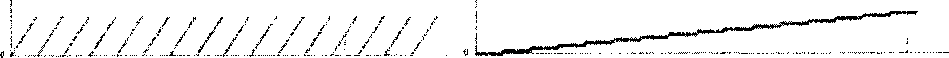


Список литературы Визуализация и анализ профиля обращений в память
- Воеводин, Вад.В. Характеристики типовых алгоритмических структур/Вад.В. Воеводин//Принято к публикации в журнал ВАК «Вестник ННГУ>. -Март-апрель 2011. -Выпуск № 2.
- Воеводин, Вад.В. Характеристики работы с памятью и эффективность работы программ/Вад.В. Воеводин//Высокопроизводительные параллельные вычисления на кластерных системах (НРС-2010): материалы X Международной конференции. -Пермь, 2010. -С. 114-118.
- Воеводин, В.В. Вычислительная математика и структура алгоритмов/В.В. Воеводин. -М: Изд-во МГУ, 2006. -112 с.
- Документация по программному инструменту ThreadSpotter компании Acumem. URL: http://acumem.com>. (дата обращения 9.02.2011)
- Корж, А.А. Оценочное тестирование современных систем и постановка задачи разработки суперкомпьютеров с перспективной архитектурой: докл./А.А. Корж.//«Научный семинар Parallel.ru», НИВЦ МГУ, 2008. URL: http://agora.guru.ru/parallel/files/MemoryWall-l_22-12-08.zip (дата обращения 9.02.2011)
- Документация по программному средству Vampir. URL: http://www.vampir.eu/(дата обращения 9.02.2011)


