Влияние масс концевых точек на динамику пятимассовой большой орбитальной космической системы цепочечной структуры

В работах [4–7] приведены результаты исследования динамики свободного орбитального движения больших орбитальных космических систем (БОКС), в том числе системы, состоящей из пяти материальных точек, соединенных шарнирно невесомыми стержнями и образующих четырехзвенную цепочку. В работах [4, 6] для начального мгновеннопоступательного состояния системы, когда пять точек БОКС расположены на дуге окружности в вертикальной плоскости транспортирующей системы координат, численным интегрированием дифференциальных уравнений движения установлены особенности движения точек и стержней БОКС на заданном

*Работа выполнена при финансовой поддержке РФФИ (грант № 14-01-96019).

промежутке времени [ t 0 , T ] . Исследования проводились в предположении, что массы точек равны и длины стержней одинаковы.

Особенностью поведения космических систем рассматриваемого вида является хаотический характер вращательных движений стержней в механической системе с большим числом степеней свободы. На параметры этого движения определяющее влияние оказывают массы точек, длины стержней, нелинейность гравитационного поля и дифференциальных уравнений движения системы и, естественно, начальные условия при численном моделировании.

1.    Описание механической системы

Рассматривается движение механической системы S , состоящей из M i ( i = 1,5) материальных тел, соединенных последовательно 4 невесомыми стержнями с длинами

I j ( j = 1,4 ) . Тела принимаются за материальные точки массами m i ( i = 1,5). Точки движутся в плоскости в центральном гравитационном поле. Длины стержней достаточно велики, их размер позволяет отнести систему S к БОКС цепочечной структуры.

Система совершает свободное движение в орбитальной плоскости под действием центральной ньютоновской силы. Для изучения динамики БОКС при численном моделировании принято:

– длины четырех стержней одинаковы и равны l (при этом 4 1 <<  H , где H - начальная высота точки M ₁ над поверхностью Земли);

– для анализа относительного движения введена подвижная поступательно движущаяся система координат Oxy – транспортирующая система координат (ТСК) [1–3] (рис. 1);

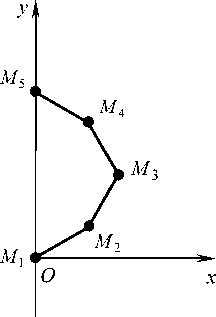
Рис.1. Начальное положение БОКС в ТСК

– начало ТСК совпадает с опорной точкой О , в качестве которой принята первая точка M ₁ пятиточечной БОКС;

– начальная скорость опорной точки соответствует ее местной круговой скорости:

стной горизонтали против вектора скорости опорной точки, а ось Oy – по местной вертикали;

– в начальном положении пять точек БОКС расположены на дуге полуокружности в первой четверти ТСК, первая точка – опорная находится в начале координат, пятая – на оси Oy (рис. 1);

– время свободного движения БОКС соответствует двум оборотам системы вокруг опорной точки, что соответствует одному обороту вокруг гравитационного центра.

• 2.    Исследование влияния масс концевых точек на движение 5-массовой БОКС в транспортирующей системе координат

В настоящей работе рассматривается влияние увеличения масс концевых точек системы на ее динамику при неизменных, по сравнению с [4, 6], остальных условиях, эволюция положений БОКС рассматривается на том же промежутке времени T .

Приведем результаты анализа движения БОКС в двух случаях.

Первый случай

Массы первой (опорной), второй, третьей и четвертой точек одинаковы, а масса пятой точки в 1,71 раза больше:

т 1 = т 2 = т 3 = ^т 4 = ^т , ^т ₅ = 1,71 ^т ; (1)

На рис. 2, 3 показана общая картина последовательных положений БОКС с шагом T /12 . На рис. 2 от начального положения 1 0 = 0 , до 1 6 = T / 2 , на рис. 3 от 1 6 до

• ¹ 12     ¹ .

  υ ₀

  
  

γ M

\ R з + H ’

где R ₃ – радиус Земли;

– начальные абсолютные угловые скорости всех стержней нулевые, т.е. БОКС в начальный момент движется мгновенно-поступательно;

– оси Ox и Oy транспортирующей системы координат в начальный момент совпадают с осями орбитальной системы координат опорной точки, т.е. ось Ox направлена по ме-

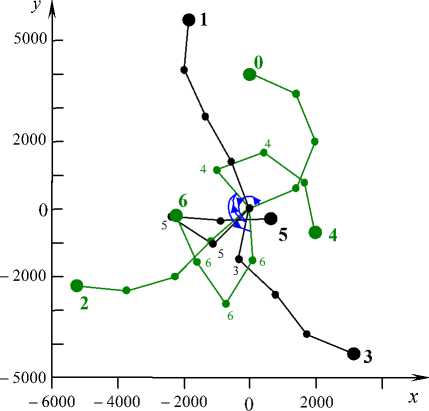
Рис. 2

Решение показывает, что на первом этапе движения при t e [ t 0 , 1 1 ] происходит распрямление начальной дуги, которую образуют точки БОКС. При этом к моменту t ₁ намечается изменение знака кривизны средней дуги y

– 2000

– 5000

– 6000 – 4000  – 2000     0      2000         x

Рис. 3

M2M5 , соединяющей точки M2, M3, M4, M5 , и дальнейшее уменьшение радиуса кривизны этой дуги до положения системы в момент t2 . К моменту t3 средняя кривизна дуги M 1M 5 меняет знак по отношению к предыдущему и к моменту t4 снова происходит смена знака средней кривизны дуги M 1M 5 . Состоя- ние системы в моменты t1 , t2 , t3 достаточно близки к соответствующим состояниям [6] для равных масс всех точек БОКС. Но различие есть, оно накапливается, и в момент t4 массивная точка M 5 , приближаясь к опорной точке M 1 , подходит к ней на расстояние в 1,66 раза ближе, чем точка M 5 в [6].

Далее картина движения БОКС существенно отличается от [6]: в то время, когда расстояние от точки M ₅ до опорной точки M ₁ после убывания к моменту t ₅ снова возрастает, и траектория точки M ₅ становится к моменту t ₆ почти замкнутой, охватывающей опорную точку, участок траектории массивной точки M ₅ в моменты t ₄ , t ₅ , t ₆ не охватывает опорную точку M ₁ (рис. 2, 4).

На рис. 4–7 приведены формы, которые принимает цепочка пяти точек для моментов t ₄, t ₅ ,..., t ₁₂ . Эти формы значительно отличаются от [4, 6] и сопровождаются большими изменениями угловых скоростей стержней, соединяющих точки.

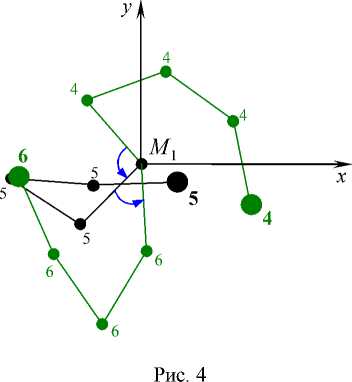
На рис. 4 форма, соответствующая моменту t ₅ , говорит о возможности возникновения в цепочке "перехлеста", когда стержни M ₂ M ₃ и M ₃ M ₄ , соединенные в средней точке M ₃ , складываются, а стержни M ₁ M ₂ и M ₄ M ₅ пересекаются. Массивная концевая точка M ₅ движется в транспортирующей системе координат почти прямолинейно (параллельно оси Ox ) в направлении орбитального движения опорной точки M ₁ , обгоняя ее.

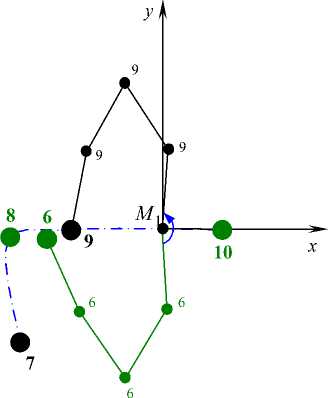
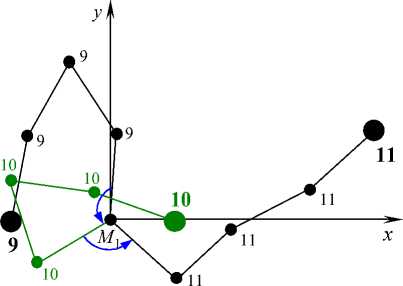
Рис. 7

На рис. 7 форма БОКС в виде «домика» при t ₉ складывается, и в момент, когда точка M ₅ перекрывает опорную, БОКС принимает форму ромба. Далее цепочка принимает форму t ₁₀ , которая, вытягиваясь, принимает вид t ₁₁ .

Рис. 5

На рис. 5 приведены положения точек системы, близкие к зеркальному относительно оси Ox , в моменты t ₆ и t ₉ . Фрагмент траектории концевой тяжелой точки M ₅ в моменты t ₇ , t ₈ ,..., t ₁₀ , когда точка M ₅ перекрывает опорную точку M ₁ , двигаясь в направлении, противоположном орбитальному движению

На рис. 8 показана траектория точки M ₅ в ТСК на рассмотренном промежутке времени T . Эта траектория не охватывает опорную точку M ₁ .

1 ^y

M ₁ 10

5r>4

x

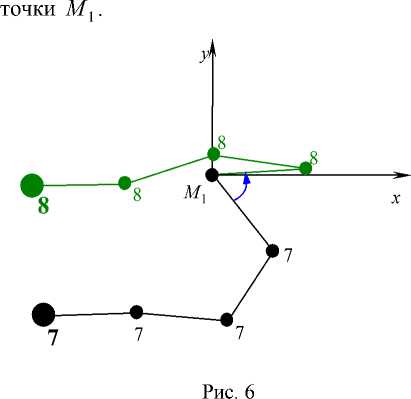
На рис. 6 при переходе из состояния t ₇ в состояние t ₈ происходит складывание первых двух стержней системы, при этом средняя точка M ₃ перекрывает опорную. Стержни M ₃ M ₄ и M ₄ M ₅ совершают почти поступательное перемещение из зоны отрицательных значений ординат точек к зоне с положительными значениями в момент t ₉ .

Рис. 8

Второй случай

Массы второй, третьей, четвертой и пятой точек одинаковы, а масса опорной точки в 1,71 раза больше:

m ₂ = m ₃ = m ₄ = m ₅ = m , m ₁ = 1,71 m .  (2)

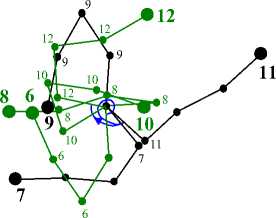
На рис. 9 и 10 показана общая картина последовательных положений БОКС с шагом

T /12. На

1 ₀ = 0 , до t 12 = ^T .

рис. 9 от начального положения

1 6 = T /2, на рис. 10 от 1 6 до

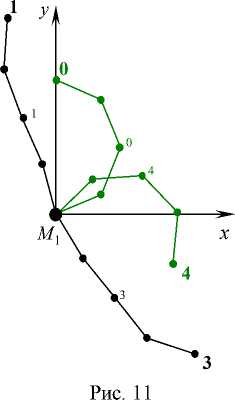
пример, пары ^{( t} 1 , t 3 ) ( t 0 , t 4 ) (Рис. 11) и пары ^{( t} 7 , t 8 ) ^{( t} 11 , t 12 ) (Рис. ^12).

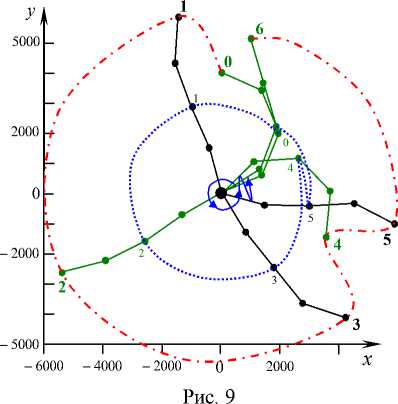
Во втором случае, когда самой массивной является опорная точка M ₁ , траектория концевой точки цепочки дважды охватывает опорную (штрихпунктирная линия на рис. 9 и 10), как и в работе [6]. Также на этих рисунках показана траектория средней точки M ₃ (точечная линия), которая имеет тот же характер, что и в работе [6].

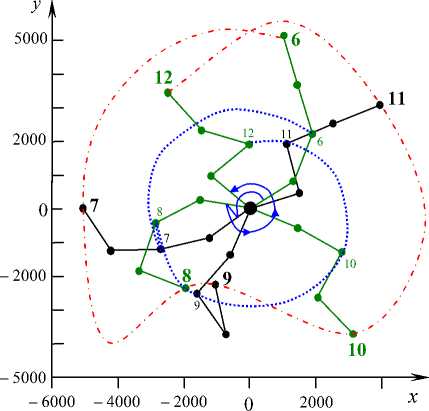
Рис. 10

Можно отметить наличие пар форм цепочки почти симметричных относительно лучей, проходящих через начало координат. На-

Общим свойством движения БОКС в случае (1) и (2) является выпрямление дуги полуокружности начального положения цепочки на промежутке t e [ t 0 , 1 3 ] (рис. 2, 9), при этом происходят незначительные изменения относительных углов и угловых скоростей соседних звеньев цепочки. Плавный характер изменения формы БОКС заканчивается при t = 1 3 в случае (1) и сохраняется до t = 1 7 в

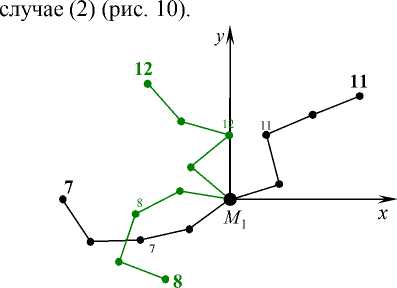
Рис. 12

Заключение

Математическая модель пятимассовой БОКС цепочечной структуры, описанная в данной работе, может быть использована для дальнейшего анализа больших космических систем.

Исследование движения 5-массовой системы проводилось численно с применением пакета Mathematica в предположении равных длин стержней, мгновенно-поступательного начального состояния системы в плоском центральном гравитационном поле. В работе рассмотрено влияние увеличения масс концевых точек системы на ее динамику. Приведено описание последовательных состояний системы в транспортирующей системе координат на промежутке двух оборотов системы вокруг опорной точки.

С использованием пакета Mathematica создана визуализация движения такой 5-мас-совой системы.