Влияние размерных параметров пор на механизмы формирования нанопленочных покрытий на подложках пористого оксида алюминия

Исследование нанопленок и нанокомпозитов является весьма, актуальной проблемой во многих областях человеческой деятельности. Благодаря своим особым свойствам, данные материалы находят применение в медицине, технике, электронике и других областях промышленности. Так, российскими учеными из Санкт-Петербургского национального исследовательского университета информационных технологий, механики и оптики и Петрозаводского государственного университета разработано уникальное нанопокрытие искусственных сосудов и стентов [1]. Уникальность покрытия заключается в возможности существенно снизить риск образования тромбов, что несомненно найдет применение в различных областях медицины и фармацевтики.

Пористый анодный оксид алюминия (АОА), благодаря гексагональноупорядоченному расположению вертикально-ориентированных к поверхности пленки пор, нашел широкое применение в качестве темплатов для синтеза наноструктур различного вида: нанопроволок, наноточек, наноколец, нанотрубок и других [2,3]. Также АОА может быть с успехом использован в качестве носителей каталитически активных наночастиц [4,5] и наноструктур полупроводников [6,7]. Это позволяет сформировать упорядоченные массивы наноструктур полупроводникового люминофора одинакового размера и формы, чтобы представить каждый нанообъект в качестве отдельного излучателя света. Когерентное сложение излучения от всех источников приведет к существенному увеличению интенсивности света [8].

Светотехнические свойства электролюминесцентных источников света (ЭЛИ) зависят от толщины слоя люминофора и его структуры. В случае ЭЛ 14, сформированных в виде нанокомпозитов типа полупроводник/диэлектрическая матрица, толщина темплата также играет большую роль, поскольку осаждаемый материал проникает в поры матрицы на глубину до 10 мкм. Вследствие этого механизм роста наноструктур в матрицах различной толщины может отличаться, и распределение легирующего элемента, а также структура люминофора, полученного методом термического осаждения смеси порошков, могут также быть различными [9].

Несмотря на большое разнообразие задач в области формирования нанопленок и наноструктур, возникающие проблемы активно решаются [10-15]. Исседования проводятся как экспериментальными методами, так и теоретическими. Методы математического моделирования позволяют оценить востребованность проведения труднодоступных и дорогостоящих экспериментов, объяснить фундаментальные законы взаимодействия наноэлементов и детально пронаблюдать динамически развивающиеся процессы в наносистеме.

Целью работы является разработка методологии исследования процессов роста нанопленочных покрытий на основе пористых подложек из оксида алюминия. Основными задачами являются: наблюдение за динамической картиной роста нанопленок, описание качественных параметров и структуры формируемых материалов, определение основных количественных, размерных и функциональных свойств массивов пористых подложек, покрытых нанопленками. Материалы, использованные для эпитаксиальных процессов, варьировались. Также в работе проводилось исследование влияния размерных параметров пор в матрице оксида алюминия на процессы зара-щивания и формирование нанопленочных покрытий.

• 1.    Математическая модель и теоретические основы

Задача осаждения нанопленок на пористые подложки оксида алюминия решалась методами математического моделирования. В условиях, когда проведение экспериментов затруднено или является дорогостоящим, проведение теоретических исследований весьма актуально. Задачи нанесения покрытий могут решаться методами квантовой механики, при помощи полуэмпирических подходов и алгоритмами Монте-Карло. Тем не менее, благодаря простоте реализации, удовлетворительной точности и небольшим затратам вычислительных ресурсов, широкое распространение получил метод молекулярной динамики (МД) [16].

Одним из основных недостатков метода молекулярной динамики является сложность сравнения результатов моделирования с реальными экспериментальными данными. Из-за малых масс атомов и молекул и высоких скоростей их движения требует- ся выбирать такой шаг интегрирования, чтобы он удовлетворял условиям сходимости и устойчивости. В большинстве случаев адекватные результаты дает шаг 0,5-2,0 фс. Таким образом, для сопоставления результатов с экспериментом требуется моделировать поведение наносистем на протяжении 1015 и более итерационных шагов, что требует больших вычислительных затрат и пока невозможно на данном этапе развития компьютерной техники. Решить сложившуюся проблему помогают комбинированные подходы и гибридные методы. Тем не менее, использование комбинированных алгоритмов затруднено из-за необходимости согласования управляющих переменных и различной природы уравнений при совмещении нескольких подходов. Также наблюдается потеря детализации описания системы и некоторых атомарно-молекулярных эффектов из-за роста величины самих объектов и времени интегрирования, чего не происходит при использовании метода МД.

Аппарат МД предполагает использование некоторого потенциального поля, от которого зависят энергетические параметры и взаимодействие между элементами наносистемы. Среди многочастичных потенциалов в последнее время активно используются: потенциал Стиллинжера - Вебера [17]; потенциал Абеля - Терсоффа [18]; метод погруженного атома [19-21]; модифицированный метод погруженного атома [22]. В данной работе использовался потенциал из модифицированного метода погруженного атома (МЕАМ - modified embedded-atom method), который основывается на теории функционала электронной плотности (DET).

В методе МЕАМ полная энергия системы записывается в виде суммы энергий отдельных атомов [23]:

E=Е Ei = Е Fi (р■Н1 Е Ф» (rij) •              W i             i \                 j=i где E - полная энергия системы; Ei - энергия атома i, используется для вычисления сил взаимодействия атомов в уравнениях движения; Fi - функция погружения для атома i, находящегося в среде с фоновой электронной плотностью рi; ф^ (rij) - парный потенциал между атомами i и j, находящимися на расстоянии rij.

В (1) функция погружения Fi ( рi ) определяется как

Fi ( рi ) = AiEi¹ ( р_г ) ln( рi ) ,                                    (2)

где Ai - регулируемый параметр; Ei - энергия сублимации; рi - фоновая электронная плотность. Данные параметры зависят от элементарного типа атома и относятся к атому типа, i.

Фоновая электронная плотность рi включает в себя вклады парциальных электронных плотностей: сферически-симметричной электронной плотности р ⁽⁰⁾ и угловых (орбитальных) вкладов р ⁽¹⁾ , р ⁽²⁾ , р⁽\ Описанные электронные плотности соответствуют s, p, d, f атомным орбиталям.

Для получения полной фоновой электронной плотности необходима комбинация или функциональная зависимость от одноэлектронных плотностей. Данную зависимость описывают различными способами, но часто используется следующее выражение, которое включает в себя угловые зависимости:

р ⁽⁰⁾

рi = ^р^G (Г i ) .                                  (3)

ρi

В выражении (3) р ⁰ является фоновой электронной плотностью исходной структуры. Величины и смысл функций G (Г i ) и Г i подробней изложены в [22-24].

Фоновая электронная плотность исходной структуры вычисляется по следующей формуле:

р0 = Pi0Zi0G (Г'ef),(4)

где pi о - масштабирующий коэффициент для плотности, зависящий от типа элемента; Zi о -число ближайших соседей атома, i в кристалличес-кой структуре: Гr^ef определяется как:

Щ = ф у t _■ k > s,k >,

'

Zi ⁰ k =1

где sik > - параметр формы, зависящий от типа элемента i Параметры формы для различных структур описаны в [22].

Парный потенциал между атомами i, j определяется исходя из выражения для энергии (1), если известна зависимость энергии от расстояния до ближайших сосе дей в кристаллической решетке. Универсальное уравнение состояния записывается в виде [23]:

EU ( R, ) = -Ei (1 + a", ( ri, )) e" ^a « ⁽ r ^- >

a, = а, (| — 1) ,

где Ei,, ai, и r⁰, - параметры, зависящие от типа конкретного атома.

Исходя из уравнений (1) и (6) и того факта, что функции погружения Fi ( рi ) и F, ( р, ) на данном этапе уже известны, можно записать выражение для вычисления парного потенциала между атомами:

ф, (Г;) = Z, [2E (ri,) - Fi (Zр- ,0> (Г;)) - F,,Pa(0> (ri,)) ] , PI а (0> где Zi, - число ближаиших соседей; pi    атомная электронная плотность, соответ ствующая s симметрии.

Таким образом, в методе МЕАМ взаимодействие между двумя атомами определяется положением всех остальных атомов в системе. Автором модели МЕАМ [22,24] была разработана схема, экранирования атомов, в которой двухчастичные функции модели становятся зависимыми от экранирующей функции, учитывающей положение остальных атомов. Более подробно с моделью, а, также с выражениями для вычисления р ⁽⁰> , р ⁽¹> , р ⁽²> , р ⁽³> , р ^{а (} k > и функциями вида G (Г i ), можно познакомиться в работах автора модели [22,23] или в ранее опубликованных трудах авторов статьи по подобной тематике [25-27].

Для проведения теоретических исследований использовался программный комплекс LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator). Данный пакет программ является свободно распространяемым, способен выполнять параллельные вычисления и поддерживает математические модели различного уровня, в том числе и классической молекулярной динамики [28]. Визуализация результатов осуществлялась при помощи программы VMD (Visual Molecular Dynamics). К преимуществам VMD относится то, что пакет поддерживает многие форматы выходных и начальных данных при моделировании поведения наносистем и содержит встроенный язык программирования tel для анализа результатов [29].

Задача моделирования осаждения нанопленок решалась в несколько этапов. На первом этапе происходит формирование подложки из аморфного оксида алюминия. Формирование сплошной аморфной подложки (рис. 1 б) происходит за счет самоорганизации атомов алюминия и кислорода, которые в начальный момент времени в требуемой пропорции (А1203) были помещены в наносистему (рис. 1 а). Далее в подложке вырезается пора требуемого размера - глубины и радиуса (рис. 1 в). Пора в подложке получалась стабильной. Как показали тестовые расчеты, при релаксации в нормальных условиях и состоянии покоя она не зарастала. Осаждение атомов происходило на последнем этапе (рис. 1 г).

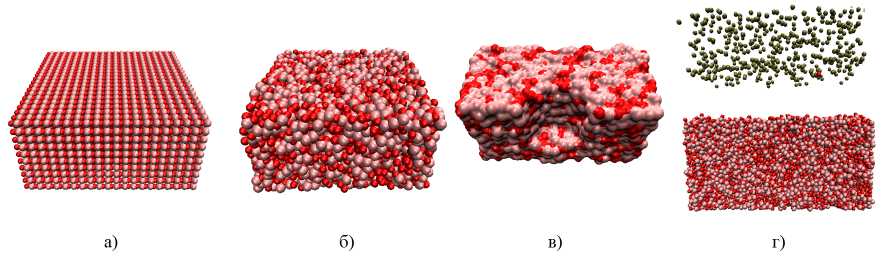
Рис. 1. Стадии исследования процессов осаждения нанопленок на пористых подложках А1203

На протяжении всех этапов решения задачи по направлениям x и у, использовались периодические граничные условия, что позволило рассматривать только одну пору в наносистеме, то есть значительно уменьшить вычислительные затраты. По оси z накладывались жесткие граничные условия, атомы не могли покинуть расчетную ячейку в этом направлении в случае отклонения от основной траектории осаждения.

Шаг интегрирования в работе был равен 1 фс (10 “ ¹⁵ с). Такая величина шага позволила адекватно отразить поведение самых быстрых и легких атомов системы. Задача моделирования поведения наносистемы решалась на протяжении 0,9 нс. Этап самоорганизации подложки (переход от рис. 1 а к рис. 1 б) длился 0,5 нс, стадия релаксации подложки с вырезанной порой (рис. 1 в) - 0,2 нс, эпитаксиальное формирование нанопленки (рис. 1г)- 0,2 нс.

Моделирование эпитаксиального процесса осуществлялось за счет добавления атомов в область над пористой подложкой. Общее количество атомов и их число в единицу времени определяли итоговую толщину нанопленки. Начальные координаты осаждаемых атомов задавались при помощи равномерного закона распределения. Первоначальные скорости частиц были одинаковы и направлены по нормали к поверхности подложки. При приближении к подложке осаждаемые атомы начинали взаимодействовать с ней, их скорости изменялись.

Термодинамические параметры наносистемы зависят от поведения каждого атома, а в частности от его массы и скоростей. Значение температуры вычисляется, исходя из разных подходов для вычисления кинетической энергии [28]:

N

T = N~_B E m. (V . )²

i =1

где N - полное число частиц пли атомов; k_B - константа, Больцмана: mi - молекулярная масса i -ro ат ома; V i = V i ( t ) - вектор скорости атома.

Давление наносистемы учитывает не только составляющую молекулярнокинетической теории идеального газа, но и влияние свойств реальных атомов:

P =

NkBT W

₁ N

+ з ж 52^r i • ^f i, i =1

где W - объем расчетиой области: f i - сила, действующая на, i -ый а том: r i - радиус-вектор i -oro атома. Второе слагаемое в (9) является вириалом.

Температура, и давление поддерживались на определенном уровне при помощи алгоритмов баростатов и термостатов. С точки зрения физики данные алгоритмы приводят к перераспределению энергии между атомами. Например, если температура, повышается выше заданной, то происходит отвод части энергии, в противном случае энергия системы искусственно увеличивается. С точки зрения численных и итерационных методов термостаты и баростаты влияют на координаты и скорости отдельных атомов, тем самым, приводя к перераспределению термодинамических параметров и энергии всей системы в целом.

В работе использовался баростат и термостат Nose-Hoover-a [30]. Термостат Nose-Hoover-а не приводит к переходу поступательных движений во вращательные, как, например, случается при использовании термостата, Берендсена, и основывается на введении сил трения для атомов системы:

d ² r f d Г d^ 1 т 2 Т_еж+

• -= = " ^ , i = 1 ,N, = n( T - Text ) , Q = T^, (10) dt² mi dt dt Q 4 n ²

• 2.    Результаты моделирования и их анализ

где £ - динамически меняющийся коэффициент сил трения; Q - массовый коэффициент; Text - целевая температура термостата; Т - текущая температура наносистемы; т_т - период осцилляций.

Начальные скорости атомов вычислялись, исходя из распределения Максвелла. Распределение Максвелла, устанавливает случайным образом скорости частиц так, чтобы кинетическая энергия наносистемы соответствовала, некоторой начальной температуре. При этом средняя скорость всех атомов в направлении каждой оси остается нулевой.

При моделировании использовались аморфные подложки оксида, алюминия, имеющие следующий размер: длина, - 12,4 нм, ширина 12,4 нм, высота - 6,2 нм. Общее количество атомов в подложке после образования поры было приблизительно равно 60,5 тыс. В начальный момент времени термодинамические условия нормальные (температура, 300 К, давление 1 атм). До этапа, эпитаксии внутренние нагрузки в матрице отсутствуют. В дальнейшем температура, у подложки поддерживалась на таком же уровне.

Размеры поры варьировались. Для первой серии вычислительных экспериментов размер поры в подложке оксида, алюминия соответствовал радиусу 2 нм и глубине 4 нм. Размеры подложки не изменялись.

Нижнее основание подложки жестко закреплялось, чтобы исключить ее перемещение по расчетной области. Тем не менее, остальные атомы подложки были подвержены тепловым колебаниям, но их координаты значительно не менялись, частицы двигались вблизи состояния с оптимальной энергией.

В работе рассматривалось осаждение различных типов атомов на подложку оксида алюминия: золото (Ап), серебро (Ag), железо (Ее), галлий (Ga), германий (Ge), палладий (Pd). Количество осаждаемых атомов было равным 20000. Скорость атомов при эпитаксии составила 0,05 нм/пс. Проведенные исследования методами математического моделирования показали, что при одинаковых термодинамических и макропараметрах наблюдаются разные характерные особенности формирования нанопленок.

Осаждение атомов железа продемонстрировало, что агломерация атомов начинается еще в вакууме, затем сгруппированные структуры собираются на поверхности подложки. Рельеф формируемой нанопленки образуется не ровный, бугристый, не сплошной, с перепадами в несколько нм. Часть атомов кислорода вытягивается из подложки и взаимодействует с железом. Внутри поры также могут содержаться агломераты Ее. Результат осаждения атомов железа, периодически транслированный по осям x и у. показан на рис. 2.

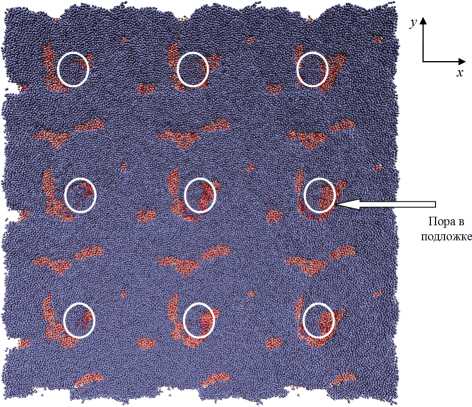
Рис. 2. Матрица подложки пористого оксида алюминия, покрытая нанопленкой из атомов железа, вид сверху, время осаждения 0,05 нс

Эпитаксиальное формирование нанопленки из атомов серебра и золота схожи между собой. Осаждение происходило равномерно, крупных структур в вакууме не образовывалось, как это было в случае с железом. Нанопленка сформировалась равномерная с небольшим проседанием в области поры. Пора осаждаемыми атомами полностью не заполнилась и оставалась полой.

Осаждение атомов германия и галлия приводило к островному формированию нанопленки, участками. Отдельно на подложке были видны сгруппированные наночастицы галлия. Вытягивание атомов кислорода происходило более активно. Визуально пора заполнялась плотнее по сравнению с другими типами осаждаемых атомов. Атомы железа, галлия и серебра при соприкосновении с поверхностью взаимодействовали с атомами кислорода, что приводило к перестроению структуры верхних слоев подложки близкой к кристаллической. Без осаждаемых атомов такое поведение материала не наблюдалось.

Покрытие поры осаждаемыми атомами происходило не всегда. При эпитаксии палладия и платины отверстие не зарастало на протяжении всего времени моделирования. Частично атомы палладия и платины попадали внутрь поры, но их количество было незначительным. Нанопленка формировалась равномерная.

Для всех типов осаждаемых атомов интенсивность по времени проникновения в пору была различной. В начальные моменты времени (до 90 пс) она была выше, и после 120 пс заметно снижалась. Наиболее плотно пора заполнялась атомами галлия, наименее активно - атомами палладия.

Динамика заполнения поры осаждаемыми атомами видна на рис. 3, на котором приведены графики глубины центра масс атомов, проникших в пору. Глубина центра масс вычислялась только по отношению к атомам, заполнившим пору. Поэтому в начальные моменты времени (до 20 пс) наблюдается большее смещение центра масс. Впоследствии число проникающих в пору атомов растет, происходит смещение зависимостей на рис. 3 в сторону середины глубины поры. Самой значительной глубины смещение центра масс достигается при осаждении атомов железа и галлия.

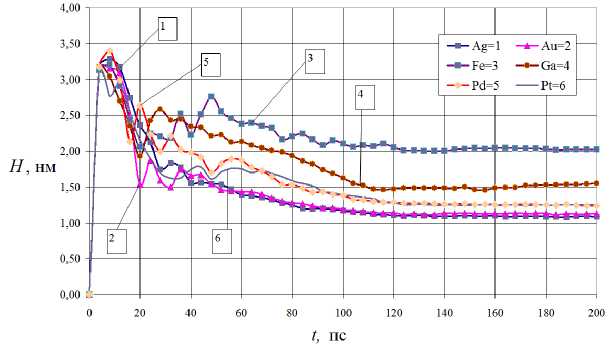
Рис. 3. Глубина центра масс атомов, проникших в пору

Для следующей серии вычислительных экспериментов радиус поры в подложке варьировался, глубина оставалось такой же (4 нм). Для осаждения использовались атомы галлия как одни из наиболее подходящих для формирования наноструктури-рованных объектов на подложке. На рис. 4 представлены графики попавших атомов Ga в пору в процентах относительно общего числа осаждаемых атомов. Активный рост количества атомов в поре, как показывает анализ графиков на рис. 4, происходит в период времени 20-120 пс. Заращивание поры после 120 пс этапа конденсации сопровождается перестройкой атомарной структуры, что соответствует стабилизации зависимостей, и небольшим уменьшением процента атомов, проникших внутрь поры.

Кроме того, при заращивании атомами галлия пор различного радиуса стабилизация центра масс осаждаемых атомов происходит на разной глубине поры (рис. 5). Для пор радиусом 2 и 3 нм центр масс формируется выше середины глубины поры. С ростом размера поры центр масс начинает образовываться в одном месте, вблизи середины глубины поры. Данный факт позволяет говорить о том, что дальнейший рост

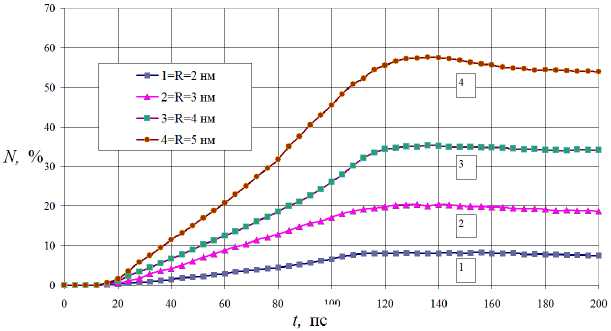
Рис. 4. Процентная доля атомов Ga в порах различного размера по отношению к общему числу осажденных атомов

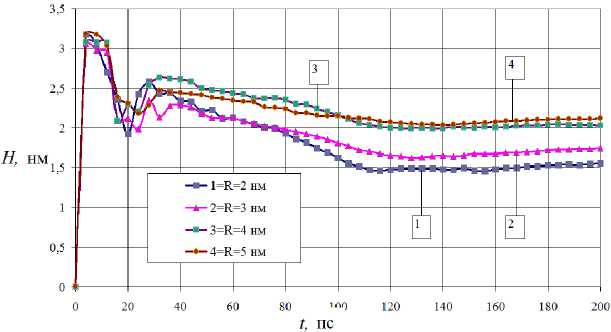
Рис. 5. Глубина центра масс осажденных атомов Ga в порах различного радиуса радиуса поры (больше 5 нм) существенного влияния на центр масс уже оказывать не будет, пора уже достаточно плотно заполнена осаждаемыми атомами.

Выводы и заключение

Представлены уравнения потенциала модифицированного метода погруженного атома, которые позволяют решить задачу нанесения нанопленок на пористые подложки с достаточной точностью. Описанная математическая модель позволяет наблюдать за кинетикой процессов формирования нанопленок и детально отследить поведение каждого атома. Приведены основные этапы осаждения наноразмерных пленок на подложки пористого оксида алюминия.

Проведенные исследования показали наличие различных механизмов формирования нанопленок на пористых подложках в зависимости от типа эпитаксиальных атомов. Осаждение атомов железа продемонстрировало, что агломерация атомов начинается еще в вакууме, затем сгруппированные структуры собираются на поверхности подложки. Рельеф нанопленки образуется не ровный, с перепадами в несколько нм. При эпитаксии атомов серебра и золота нанопленка формируется равномерная с небольшим проседанием в области поры, крупных структур в вакууме не образу- ется. Осаждение атомов германия и галлия приводило к островному формированию нанопленки, участками. Отдельно на подложке были видны сгруппированные наночастицы галлия. В процессе напыления палладия и платины отверстие не зарастало на протяжении всего времени моделирования, нанопленка формировалась равномерная.

Для всех типов атомов единичные атомы достигали дна поры. При нанесении атомов галлия на подложку наблюдалось наиболее полное и плотное заполнение поры. Пористые подложки с нанесенными нанопленками могут рассматриваться как массив квантовых точек и использоваться для получения оптических и электрических эффектов.

При исследовании заращивания атомами галлия покрытий с порами различного размера было получено, что активный рост количества атомов в поре происходит в период времени 20-120 пс. Заращивание поры после 120 пс времени конденсации сопровождается перестройкой атомарной структуры, что соответствует стабилизации зависимостей, и небольшим уменьшением процента атомов галлия, проникших внутрь поры. Кроме того, стабилизация центра масс осаждаемых атомов происходит на разной глубине поры. Для пор радиусом 2 и 3 нм центр масс формируется выше середины глубины поры. С ростом размера поры центр масс начинает образовываться вблизи середины глубины поры. Дальнейший рост радиуса поры (больше 5 нм) существенного влияния на центр масс не оказывает, пора уже достаточно плотно заполнена осаждаемыми атомами.

Приведенные методики и полученные результаты могут быть применены при разработке новых перспективных слоистых композитов на основе пористых подложек, изучения их характеристик, а также для проектирования нанопленочных материалов и алгоритмов прогнозирования свойств.

Исследование выполнено при финансовой поддерэюке РИФ (проект № 15-1910002).