Влияние скоростных связей на устойчивость равновесия динамической системы резания

Введение. Существует два основных механизма потери устойчивости динамической системы резания. Один связан с непотенциальностью позиционных сил, формируемых процессом резания. В этом случае на устойчивость системы влияют формируемые естественным образом циркуляционные силы, связанные с кососимметричными суммарными матрицами упругости подсистемы инструмента и процесса резания. Второй обусловлен влиянием матрицы скоростных коэффициентов в динамической связи, формируемой процессом резания. Скоростные коэффициенты формируются в результате двух принципиально различных факторов. Во-первых, они зависят от запаздывающих аргументов изменения сил от координат упругих деформационных смещений. Запаздывающие аргументы имеют двоякую природу: запаздывание сил от деформационных смещений, формируемых в области первичной пластической деформации; дисбаланс сил в области первичной пластической деформации и сил, формируемых в области вторичной пластической деформации, что вызывает переходные процессы в области вторичной пластической деформации, направленные на уравновешивание указанных сил. Поэтому запаздывание силы F2 характеризуется меньшим временем запаздывания по отношению к силе F1 [1 – 3]. Запаздывание сил F1 по отношению к силам F2 отмечается во всех известных экспериментальных исследованиях. Во-вторых, они свя- заны с существованием участков с падающими зависимостями сил от скоростей. Необходимо учитывать, что падающие участки скоростной зависимости сил обусловлены действием так называемого температурно-скоростного фактора, учитывающего, с одной стороны, влияние скорости на производство тепла, с другой – влияние температуры на физико-механические характеристики материала в зоне резания.

Постановка задачи. Если ограничиться формальными представлениями не раскрывая механизмы формирования матриц скоростных коэффициентов, необходимо проанализировать влияние матриц скоростных коэффициентов на устойчивость точки равновесия системы. Для этого обратимся к базовой динамической модели процесса резания, обоснование которой было дано ранее в [1]:

где X

–

d2X m dt2

/ ^dX х/ Г 1 у ^dX / I + h — + cX = F\ X , — , а , b , dt          l dt J

упругие деформационные

координаты без процесса резания,

теризующие e U dX к

F X,   ,а,b l dt

динамическую

смещения вершины инструмента относительно ее

X = {X 1 ,X 2 } T ; F | X , dX , а , b | - вектор-функции, харак- l dt )

связь,

e U dX         dX к

F ¹ 1 X , dt ' а , b I , F ² 1 X , dt ' а , b

формируемую процессом

T

резания,

; a , b – толщина и ширина срезаемого

слоя, зависящие от величины подачи на оборот и глубины резания при заданных геометрических параметрах инструмента соответственно; m, h, c – матрицы инерционных, скоростных и упругих коэффициентов подсистемы инструмента без процесса резания соответствен- но,

m =

m 0

m

h 1,1 h 1,2

h²¹ 1 c ₌ [ c i,i c 2,1 h 2,2 J '       ^1,2 c 2,2

Матрицы m, h и c симметричные и положительно определенные. Следовательно, при e U dX к Fl X, —,а,b к dt

= 0 система (1) имеет единственную точку равновесия X* = {0,0}т, которая яв- ляется асимптотически устойчивой. Необходимо выяснить, при каких условиях равновесие системы (1) является асимптотически устойчивым. Для этого необходимо проанализировать уравнение в вариациях относительно точки равновесия X* = {X*, X2}т, определяемой из системы (1) для установившегося состояния cX * = F (X * ,0, а, b).

Таким образом, точка равновесия в динамической системе резания при заданной геометрии инструмента и матрице упругости c зависит от технологических режимов, которые определяют параметры a и b .

Уравнение в вариациях относительно точки равновесия X* = {X*, X2}т для малых откло- нений

x ( t ) = X ( t ) — X -

в линеаризованном представлении получаем из (1) с учетом (2)

d2x    dx m —- + h — + cx = 0, dt2 z dt 1

где c _x

—

— с1,1

с 1,2

дф 1	с — дФ 1_ 2,1    д х 2		h	ЭФ 1 —	h	ЭФ 1 —
д х 1		, h =	h 1,1	Э Х 1	h 2,1	д;с 2
дф 2	с  — .Эк	, I	h	ЭФ 2 —	h	ЭФ 2 —
д х 1	2,2    д х 2 _		_ 1,2	д Х 1	2,2	д Х2

, ф ( х ) = F(X , dX / dt , а , b ) — F ( X * ,0, а , b ).

Изучим условия потери устойчивости за счет вариации параметров h^). Система в вариа циях относительно точки равновесия в предположении, что с * k) = 0, имеет вид d2x     dx           dx

m —- + h (c ) — + c'^c ) x + h (^k ) — = 0.

dt ^{2     z} dt ^{z ?} dt

Известно, что при условии, когда матрицы с ^ ) и m являются симметричными и положительно определенными, система имеет устойчивую, согласно Ляпунову, точку равновесия. Добавление к системе связей, формируемых матрицей h ( ^c ) , преобразует устойчивую по Ляпунову систему в асимптотически устойчивую при условии, что матрица h ( ^c ) является положительно определенной. Известно, что в этом случае система имеет полную диссипацию [4]. Поэтому необходимым условием устойчивости равновесия системы является положительная определенность матрицы h ( ^c ) . Пусть задана матрица h

^{[ h} 1,1 + ^h 1P ] ^{[ h} 2,1 + ^h 2⁽,? ] . ^{[ h} 1,2 ⁺ h iT ] ^{[ h} 2,2 ^{+ h}y^]

где h - матрица демпфирования подсистемы инструмента, h =

^{[ h} 1,1^]

^{[ h} 1,2^]

^{[ h} 2,1^]

^{[ h} 2,2^]

h ^{( Р )} – матрица ско-

ростных коэффициентов, формируемая процессом резания, h ⁽ Р ) =

_{[ h 1}(_, Р ₁)_]

_{[ h 1}(_, Р ₂)_]

_{[ h 2}( Р _,1)_]

_{[ h 2}( Р _,2)_]

зания

Получаем условие положительной определенности h ( ^c )

( h _u + h ^ )( h 2,2 + h P ) - [ h 1,2 + 0, 5(h⁽ P + h 2 ? )] ² >  0.                         (6)

При этом не принимается во внимание матрица h ^k ) =

- 0,5( h 2 P - h ^) )

0,5( h 2 P - h i p ) )

в (5).

Однако еще Кельвином и Тетом доказано [4], что гироскопические силы, формируемые матрицей h(k), лишь улучшают асимптотическую устойчивость системы при выполнении условия (6). Ими же доказано, что если условие (6) не выполняется, то гироскопические силы не могут стабилизировать равновесие системы. Поэтому условие (6) для системы (4) является также достаточным для обеспечения асимптотической устойчивости системы резания.

Например, если рассматривается процесс резания, у которого отношение величины подачи на оборот к глубине резания (отношение толщины срезаемого слоя к его ширине) есть величина малая, то условие (6) определяется выражением h1,1

—

T F || h

¹ 5 X 1Л ^2,2

—

—

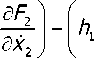
0,5 T ^F^ ^

² 8 X 1 J

> 0,

где T ₁ – запаздывающий аргумент, определяющий запаздывание, формируемое в области первичной пластической деформации; T ₂ – запаздывающий аргумент, определяющий запазды-

„                            „              „               „                 dF вание вариаций сил в области первичной и вторичной пластической деформаций; 2 – ко- dx 2

эффициент, определяющий приращение тангенциальной силы, обусловленное приращением скорости резания при тангенциальных колебаниях инструмента относительно заготовки.

Анализ (7) показывает, что за счет матрицы скоростных коэффициентов, формируемой динамической связью, образованной процессом резания, существует множество сценариев, при которых эта система может потерять устойчивость, во-первых, при увеличении коэффициента dF2

d X₂

. Этот вопрос проанализирован в работах [5 – 7]. В скалярных моделях этот механизм потери устойчивости приводит к анализу уравнений Ван дер Поля или Рэлея, которые использовались для объяснения формирования автоколебаний при резании в работах [5 – 7]. Во-вторых, система резания может потерять устойчивость при увеличении коэффициента

T F

1 9 x 1

зависящего как от

соответствующего коэффициента матрицы жесткости процесса резания, так и от величины запаздывания T1 . Этот механизм согласуется с данными В.А. Кудинова и его учеников [8]. Однако в отличие от этих работ анализ (7) показывает, что увеличение запаздывающего аргумента влияет на устойчивость не столь однозначно, так как при увеличении T1 возрастает и величина T2 .

При этом необходимо учитывать, что в динамических системах резания обычно выполня-dF   dF ется условие —- » —L. Кроме этого, все модели потери устойчивости, основанные на гистере-0X 2   0X1

зисных свойствах изменения сил при внедрении инструмента в заготовку и при его выходе, фактически рассматривают пространственное запаздывание [9 – 11]. Поэтому при заданной частоте его можно учесть и на основе временного запаздывания. Приведенный анализ показывает, что рассмотрение механизмов потери устойчивости на основе выполненных исследований, опирающихся на фундаментальные представления механики, позволяет не только учесть все известные механизмы потери устойчивости, но и существенно их дополнить.

Проанализируем возможность потери устойчивости процесса резания в результате связи между циркуляционными силами и матрицей скоростных коэффициентов. Выполненные выше рассуждения предполагали, что с * k) = 0 . Теперь учтем, что с * k) * 0. Проанализируем систему m d X + h(c) — + c(cc) x + h*k) — + c'k) x = 0,

dt2     *  dt *       *  dt *'

для которой выпишем характеристический полином в виде

A(P) = P(P) + 0,S(h2P) - h^c)p + 0,25(5c)2,(9)

где P ( p ) – характеристический полином системы, т. е. системы без циркуляционных сил,

^P( P) = ⁽ mP ² + h y, * P + c y, * )( mP ² + h 2,2, * P + C ^, * ) ^{- ( h} 2,1, * ^h 1,2, * )P 2 ^- 0, 5^{( h} y, * + ^h i2 * ^{)( c} 2,y + c i2 * )P ^- - 0,25( c 2,1, * + c₁₂ * ) ² ; 5 - коэффициент жесткости, характеризующий асимметрию матрицы жесткости системы резания, 5 c = с 2,1, * - с₁₂ * = с 2,11) - с 1Р .

В (9) учтено, что в подсистеме инструмента матрица m является диагональной, а матрицы h = [ h _s , _k ] , s , k = 1,2 и c =[ c _s , _k ] , s , k = 1,2 симметричны. Кроме этого, матрицы h * с ) =^ h sck , * ] , s , k = 1,2, c * ^с ) =[ c Sck , * J , s , k = 1,2 - положительно определенны. Гироскопические члены, формируемые кососимметричными составляющими матрицы скоростных коэффициентов, лишь улучшают асимптотическую устойчивость системы, поэтому можно утверждать, что все корни характеристического полинома P ( p ) расположены в левой комплексной полуплоскости. Поэтому для определения устойчивости системы (8) необходимо выяснить преобразование корней за счет члена 0,5( h ₂ ⁽ p ) - h ₁⁽, p ⁾ )( 5 c ) p + 0,25( 5 c ) ² . Для этого удобно воспользоваться критерием устойчивости Михайлова [5]

H( j rn ) = P ( j rn ) + 0,5( h ₂ ^{( P )} - h 1^{( p )} )( 5 c ) j ю + 0,25( 5 c ) ² .

Годограф Михайлова системы (8) P ( j ω ) преобразуется в годограф H ( j ω ) системы (8) за счет члена 0,5( h ₂ ^{( P} _,1 ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ )( δ c ) j ω + 0, 25( δ c ) ² (рис. 1). На приведенной иллюстрации характер преобразования годографа Михайлова принципиально зависит от знаков и величин параметров h ₂ ^{( P} _,1 ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ и δ c . Если гироскопические члены отсутствуют ( h ₂ ⁽ _, ^P ₁ ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ = 0 ), то исходный годограф смещается, как показано на рис. 1 пунктиром. Если параметры h ₂ ^{( P} _,1 ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ и δ c имеют различные знаки, то гироскопические члены совместно с циркуляционными лишь ухудшают устойчивость равновесия. В этом случае годограф P ( j ω ) преобразуется в годограф H ₂ ( j ω ) . Если параметры h ₂ ^{( P} _,1 ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ и δ c имеют одинаковые знаки, то гироскопические члены могут стабилизировать равновесия системы, если точка равновесия потеряла устойчивость из-за циркуляционных членов. В этом случае годограф P ( j ω ) преобразуется в годограф H ₁ ( j ω ) .

Im( ω )

∞←ω

H ₁ ( j ω )

Re(0)

¹₄(δ c )²

Re( ω )

P ( j ω )

H ₂ ( j ω )

Рис. 1. Преобразование годографа Михайлова P ( j ω ) в годограф H ( j ω )

Раскроем смысл асимметрии матриц скоростных коэффициентов и матриц упругости со стороны процесса резания. Коэффициент h ₁ ⁽ _, ^P ₂ ⁾ = - T ₂ c ₁ ⁽ _, ^P ₂ ⁾ обычно является отрицательным и значительно превышает h ₂ ^{( P} _,1 ⁾ . Поэтому для традиционной схемы процесса резания можно принять, что h ₂ ⁽ _, ^P ₁ ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ >  0 . Коэффициент δ c = с ₂ ^{( Р} _,1 ⁾ - с ₁ ⁽ _, ^Р ₂ ⁾ <  0, так как с ₁ ⁽ _, ^Р ₂ ⁾ >  0 и с ₂ ^{( Р} _,1 ⁾ <  с ₁ ⁽ _, ^Р ₂ ⁾ . Это связано с тем, что с ₁ ⁽ _, ^Р ₂ ⁾ определяется отношением приращения тангенциальной силы к смещению инструмента в нормальном направлении. Что касается коэффициента с ₂ ^{( Р} _,1 ⁾ , то он характеризует приращение нормальной силы к тангенциальным смещениям. Таким образом, характерный для резания случай соответствует различным знакам при коэффициентах h ₂ ^{( P} _,1 ⁾ - h ₁ ⁽ _, ^P ₂ ⁾ и δ c . В этом случае формирование гироскопической связи совместно со связью, формирующей циркуляционные силы, лишь ухудшает устойчивость системы.

Важно подчеркнуть, что формирование циркуляционных и гироскопических сил взаимосвязано. Кроме этого, коэффициент с ₁ ⁽ _, ^Р ₁ ⁾ матрицы жесткости процесса резания влияет на коэффициент h _{1,1, Σ} матрицы скоростных коэффициентов.

Анализ областей устойчивости в плоскости варьируемых параметров динамической характеристики процесса резания. Для оценки влияния матрицы скоростных коэффициентов на устойчивость системы удобно воспользоваться методом D-разбиения. Рассмотрим преобразо- вание областей устойчивости динамической системы резания для наиболее важного случая, когда изгибными деформационными смещениями инструмента, а также зависимостью сил от вариаций скорости резания можно пренебречь. Кроме этого, примем во внимание, что запаздывание T2 изменения сил, действующих в тангенциальном направлении, меньше, чем запаздывание T1 в нормальном направлении, т. е. T1 > T2. В этом случае матрицы жесткости и скоростных коэффи- циентов в развернутом виде соответственно равны: h

' h_v — C P T  h ₂ ,1

( P )

1,2    c 1,2  2     2,2

( P )

^c 1,1 + ^c 1,1 c 2,1

( P )

^c 1,2 + ^c 1,2 c 2,2

При T1 = T2 = 0 области устойчивости проанализированы [1]. Выясним изменения областей за счет параметров T1 и T2 . Характеристический полином системы в этом случае можно представить в виде

^{А (} p ) = ( mp ² + h^ p + c _w + c P ) ( mp ² + ^h 2,2 P + c 2,2 ) — ( ^h 1,2 P + ^C 1,2 + c^ ) ( ^h 2,1 P ■ c 2,1 ) ^-

^Tc 1 ^P p ( mp ^{2 + h} 2,2 p ⁺ c 2,2 ) ^{+ T} 2 cv 2 p ( ^h 2,1 p ⁺ c 2,1 ) ] .

Тогда в плоскости двух варьируемых параметров T1 и T2 уравнение фигуративной линии будет иметь вид

( - с Р^h 2,2 ® ² ) ^T 1 ■ ( c P ^h 2,1 ® ² ) ^T 2 =

2_m4 -Гт fr( Р )+r                       2    2         _r( p )V            _r( p )\_r

= m to     ^m ( с^ + C 1,! + c 2,2 ) + ^h 1,1 ^h 2,2    ^h 1,2 J ® ⁺ ( c 1,1 ⁺ c 1,1 ) c 2,2    ( c 1,2 ⁺ c 1,2 ) c 2,1 ,

(C !^: P ) c ₂to - c^{p p} ) m to ³ ) T + ( c^p P ) c _tto) T = 1,1   2,2         1,1              1        1,2   2,1       2

= to^{[ h} 2,2 ( ^C 1,1 + ^C 1⁽, ^{P )} ) + ^h 1,1 c 2,2 ^{- 2 h} 2,1 c 1,2 ^{- h} 2,1 ^C l ^P 2) ]^- m ( ^h 1,1 ^{+ h} 2,2 )to 3 .

Рассмотрим примеры преобразования областей устойчивости при изменении параметров T ₁ и T ₂ (рис. 2) для системы, параметры подсистемы инструмента которой приведены в таблице.

Диаграммы соответствуют устойчивой системе при T 1 = T ₂ = 0 и с 2 Р 1) = с 2 Р ₂) = 0. Однако в зависимости от параметров T ₁ и T ₂ система может потерять устойчивость.

Параметры исходной системы без резания

m , кГ • с 2 / мм			h , кГ • с / мм			c , кГ / мм
	" 10 - 3 0 " _ 0 10 - 3 ]			" 0,1 0,14 " _ 0,14 0,4 ]			[ 2000 - 800 " _- 800 1000 _

Фигуративная линия представляет собой петлеобразную кривую, принципиально разбивающую плоскость T ₁ и T ₂ на три области. Устойчивая область обозначена на рис. 2. Во всех остальных областях система неустойчива, причем в области петли характеристический полином системы имеет на четыре корня с положительной вещественной частью больше, чем в области устойчивости, в остальной части – на два корня. Таким образом, потеря устойчивости системы имеет колебательный характер.

Когда в подсистеме инструмента деформационным смещениям в направлении X ₂ дополнительно соответствуют изгибные деформации инструмента, в матрице динамической жесткости процесса резания значимыми являются коэффициенты второго столбца, т. е. с ₂ ^{( Р} _,1 ⁾ и с ₂ ^{( Р} _,2 ⁾ , а по мере изменения этих коэффициентов наблюдается сужение области устойчивости (рис. 2). Направление изменения фигуративных линий показано стрелками. В данном случае учитывается, что постоянные времени, определяющие запаздывание сил по отношению к деформационным смеще- 1174

ниям инструмента относительно заготовки, для составляющих сил F ₁ и F ₂ различны. Если полагать, как это предложено в работе [8], что T 1 = T 2 = T , то предельные значения T определяются по прямой (на рис. 2 пунктирная линия).

T 1 , c∙10^–3

3 -

Область устойчивости

T 2 , c∙10^–3

Рис. 2. Область устойчивости в плоскости T 1 , T 2 при значениях c^p = [0, -100, -200, -300, -400], кг/мм; 2,1

c ₂ ^p _,2 =[0, -20, -40, -60, -80], кг/мм; c ₁ ^p _,2 =1000 , кг/мм; c ₁ ^p _,2 =500, кг/мм

На области устойчивости в плоскости параметров T ₁ и T ₂ оказывают влияние и коэффициенты первого столбца матрицы динамической жесткости процесса резания. В связи с этим рассмотрим также преобразование областей устойчивости по мере изменения коэффициентов с ₁ ⁽ _, ^Р ₁ ⁾ и с ₁ ⁽ _, ^Р ₂ ⁾ для случая, когда изгибные деформационные смещения инструмента отсутствуют (рис. 3). Точечными прямыми показаны направления изменения параметров T ₁ и T ₂ , имеющие постоянное соотношение между собой, T 1 = kT₂, к = 1,2,3 (рис. 3). В динамических системах резания всегда выполняется условие к >  1. Очевидно, что при неизменных значениях T 2 по мере увеличения T 1 тенденция системы к потере устойчивости возрастает. Так как по мере увеличения T ₂ возрастает асимметрия матриц скоростных коэффициентов, следовательно возрастают и кососимметричные составляющие этой матрицы, формирующие, как известно, гироскопические силы. Увеличение гироскопических сил не должно вызывать потерю устойчивости системы. Однако в динамических системах резания увеличение T ₂ происходит при одновременном возрастании T ₁ , но T ₁ увеличивается быстрее. Возрастание T ₁ приводит к тому, что после критического значения этого параметра симметричная часть матрицы скоростных коэффициентов может стать отрицательно определенной, что вызывает потерю устойчивости равновесия системы. К этому же эффекту приводит и увеличение так называемого отрицательного коэффициента трения при рассмотрении кинетической характеристики процесса. Кроме этого, вариации матриц скоростных коэффициентов связаны с вариациями матриц динамической жесткости процесса резания. Известно, что кососимметричные составляющие матриц динамической жесткости процесса резания также влияют на устойчивость системы.

Анализ показывает, что матрицы скоростных коэффициентов, формируемые линеаризованной динамической характеристикой процесса резания, оказывают сложное влияние на устой- чивость равновесия системы. Однако общая тенденция такова: по мере увеличения запаздывающих аргументов в динамической системе резания возрастает склонность к потере устойчивости равновесия. Подчеркнем, что падающая характеристика зависимости сил резания по мере увеличения скорости принципиально вызывает эффекты, аналогичные уже рассмотренным.

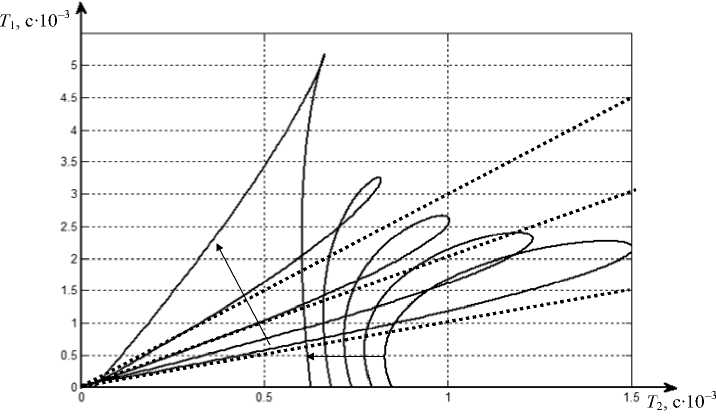
Рис. 3. Области устойчивости в плоскости T 1 , T 2 при значениях с^р 2, = 0 кг/мм, с^р 2,2 = 0 кг/мм, с^р 1,2 = 1000 кг/мм, с^р 1,1 = [500, 400, 300, 200, 100] кг/мм.

Уменьшению с^р 1, соответствует преобразование областей по направлению стрелки

Анализ областей устойчивости в плоскости варьируемых параметров технологических режимов обработки. Для практических приложений важно определить области устойчивости не в параметрическом пространстве линеаризованной динамической характеристики процесса резания, а в пространстве технологических режимов. В данном случае имеют значение два параметра: глубина резания tP и скорость VP . В традиционной схеме отработки принято, что величи- на подачи на порядок меньше, чем глубина, а варьирование подачи практически не влияет на устойчивость процесса. Можно представить параметры матриц скоростных коэффициентов и ди- намической жесткости процесса резания в технологических режимах [1 – 3]

с Р = Р 1 b = Р 1

. hP-Vt р -

tp ; с(Р) =0, b = р   tp sin(ф)'   ,             P2 sin(ф),

-t -; h P) = — ^l2- р - t -, sin( ф )     ,       V_P ^и sin( ф )

где р1, p2 - коэффициенты, характеризующие давление стружки на переднюю поверхность, спроектированное на направления X1 и X2 , кг/мм2; l1 и l2 – путь резания, необходимый для установления нового стационарного состояния системы резания при изменении деформационного смещения X1; ф - главный угол режущего инструмента в плане.

Определим характеристический полином системы

А ( p ) =

m il P ² +1 ^h11

l     tp  I                 tp

— 1 Pi      IP + C + Pi v H sin ф! , H sin ф

h 1,2

—

"2 p² " tp; v Sin Ф

l

t

P + C 2 + p₂ —

^{1,2     2} Sin Ф

^h 2,1 P ⁺ c 2,1

m 2,2 P ^{2 + h} 2,2 P ⁺ c 2,2

Перейдя в частотную область после замены p = j® (13), получим систему для вычисле ния фигуративной линии в плоскости tP - VP

^ ( ^ю ) + p a a -Л® + t p a 2⁽ ® ⁾ = 0, ^Vp

B ( ® + t p b » + t _p b 2 ( ® ) = 0,

Vp где A(®) = m^ m2,2®4 - (Clilm2,2 + ^2,2 + muc2,2 - h 2h2 .)('/ + c^c2,2 - c1,2c2,1;

3 1И = ⁽ l 1 P 1 h 2,2 ^{- 1} 2 P 2 ^h 2,1⁾ S ®n^ ; a 2 ⁽ ® ) = ⁽ P 1 c 2,2 ^- P 2 c 2,1 ^- P 1 m 2,2 ® 2 ) S^ ;

B ( to ) = ^{- ( h} 1,1 m 2,2 + m 1,1 h 2,2⁾ to ³ + ⁽ c 1,1 h 2,2 + h 1,1 c 2,2 ^- c 1,2 h 2,1 ^{- h} 1,2 c 2,1 ) ® ;

b 1 ( ® ) = ( l 1 P 1 ^ 2,2 ® 2 - I 1 P 1 C 2,2 + 1 2 P 2 C 2,1 )si ®^ ; Ь 2 ( ® ) = ( P 1 h 2,2 -P 2 h 21 ) si^ •

Приведем пример (рис. 4) границы областей устойчивости для системы, параметры которой приведены в таблице, а параметры, связывающие технологические режимы с динамическими параметрами связи, формируемой процессом резания, соответствуют p ₁ = 100 кг/мм²; P ₂ = 200 кг/мм²; 1 ₁ = 0,9 • 10 ^{- 3} мм; 1 ₂ = 2 • 10 ^{- 3}мм.

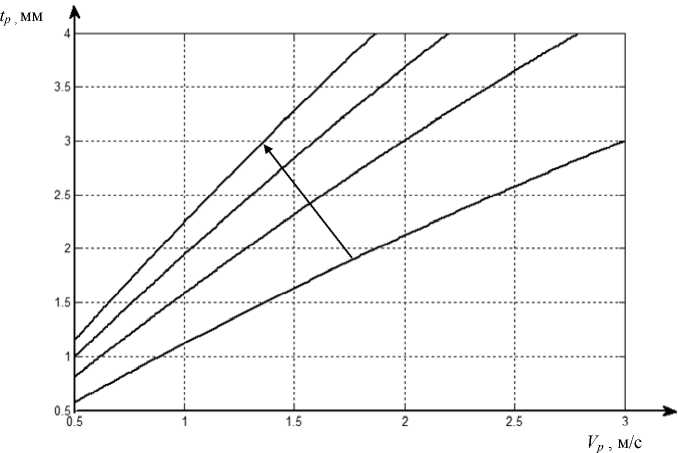
Рис. 4. Изменение области устойчивости в плоскости технологических параметров при изменении угла φ = {30°, 45°, 60°, 90°}.

Увеличению угла ф соответствует преобразование фигуративных линий по стрелке