Влияние возмущений плотности ионосферной плазмы на условия распространения электромагнитных свистовых волн в ионосфере

Процессы распространения низкочастотных электромагнитных волн свистового диапазона (от 0,5 до 10 кГц) через ионосферу к поверхности Земли могут зависеть от множества различных факторов. Основными факторами являются зависимость плазменной концентрации и пространственное распределение полей в падающей сверху волне. Однако при внешне схожих глобальных условиях характеристики волн, как отраженных, так и дошедших до поверхности Земли, могут существенно различаться [1–4]. Одна из причин различий в условиях прохождения свистовых волн через ионосферу обусловлена с неоднородностями плазменной концентрации [5–7]. В частности, неоднородности плазменной концентрации могут быть связаны с инфразвуковыми волнами.

Инфразвуковые волны генерируются молниевыми разрядами, вулканической активностью, землетрясениями, прохождением атмосферных фронтов и цунами, а также явлениями антропогенного характера – работой реактивных двигателей и др. [8]. Дисперсионное соотношение для инфразвуковых волн можно записать в виде го2 ^ с2(к2 +1 / 4H2), где Cs ® 370 м/с - скорость звука, H ≈ 10 км – высота однородной атмосферы; κ – волновое число инфразвуковой волны. Периоды инфразвуковых волн имеют порядок нескольких минут [9].

В данной работе рассматривается задача о воздействии колебаний плазменной концентрации, вызванных инфразвуковой волной, на коэффициент отражения свистовых волн от утренней ионосферы сверху и поле волны, дошедшей до земной поверхности. Для вычислений поля свистовой волны используется метод коллокаций решения граничной задачи. Анализ зависимостей коэффициента отражения свистовых волн и поля вблизи земной поверхности от характеристик регулярных неоднородностей плазменной концентрации важен для понимания взаимосвязи волновых процессов в магнитосфере. Вызванные инфразвуковыми волнами неоднородности ионосферной концентрации объясняют возможность модуляции добротности резонатора в плазменном магнитосферном мазере, режим работы которого зависит от декремента затухания плотности энергии ε свистовых волн в магнитосферном резонаторе и, следовательно, величины коэффициента отражения свистовых волн от ионосферы сверху [10; 11]. Колебательные режимы плазменного магнито-

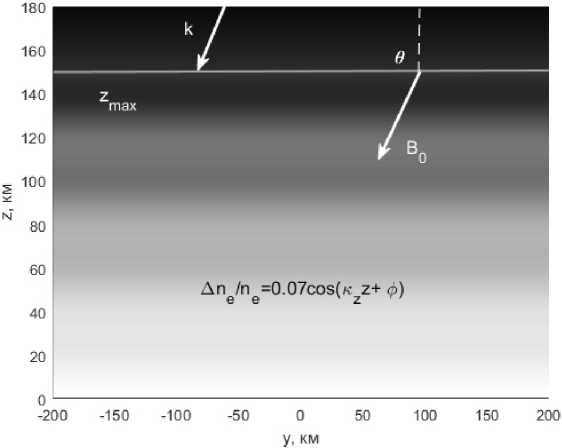
Рис. 1. Схема, поясняющая постановку задачи

Fig. 1. Scheme that illustrate the formulation of the problem

сферного мазера и свистовые излучения типичны для утренних условий, когда коэффициенты отражения свистовых волн не превышают значений порядка 0,05.

1. Постановка задачи, исходные уравнения и метод решения

Предположим, что на ионосферу падает сверху свистовая электромагнитная волна с частотой го. Пусть ось z направлена вертикально вверх, значения z = 0 и z = z max соответствуют поверхности Земли и поверхности падения свистовой волны, магнитное поле Земли лежит в плоскости y, z и составляет с осью z угол 9. Ионосферную плазму выше границы z > zmax будем считать однородной. Рассмотрим задачу о влиянии малых возмущений плазменной концентрации в инфразвуковой волне на процессы распространения свистовой волны. Для плазменной концентрации используем модельную зависимость ne (z, r± ) = ne о (z) + A ne cos( к zz + Ф t)), (1) где первое слагаемое определяет невозмущенную концентрацию ne0(z), а второе связано с ее слабым (|Лne| « ne0) возмущением в инфразвуковой волне. Частоту инфразвуковой волны будем считать пренебрежимо малой по сравнению с частотой свистовой волны и рассматривать величину ф(t) как параметр, не изменяющийся за время исследуемых процессов. Схема, поясняющая постановку задачи, приведена на рис. 1.

В случае зависимости вида (1) ионосферу можно определять как плоскослоистую анизотропную

среду с тензором диэлектрической проницаемости [12]:

£ =

£ igcos 9

- ig sin 9

- ig cos 9

£ cos 9 + n sin 9

( p-s )sin 9 cos 9

ig sin 9

( p-s )sin 9 cos 9 s sin ² 9 + n cos ² 9

где в приближении «холодной плазмы»

s = 1 -

®2e (®+ i ve) p го((го + ive )2 -ro|e)

^ro Pi ^{( ro +} i ^v i ) ro (( ro + i v i ) ² -ro |i )

П = 1 -

g =

^ro pe          ^ro pi

---- ro(ro + iv e) ro(ro + ivi)

^ro Pe ^ro Be ^ro P ^ro Bi       ;

ro (( ro + i v e ) ² -ro |e )    ro (( ro + i v i ) ² -ro |i )

ro pe и ro pi - электронная и ионная плазменные частоты; ro ie и ro ii - величины электронной и ионной гирочастот; v _e и v _i - частоты электронных и ионных столкновений с нейтральными частицами.

Учитывая, что в плоскослоистой среде поперечная компонента волнового вектора k ₁ сохраняется, напряженности электрического и магнитного полей свистовой волны представим в виде E ( z )exp i ( k _± r ₁-ro t ), H ( z )exp i ( k _± r _±-ro t ). Тогда из уравнений Максвелла получаем систему уравнений для поперечных компонент поля E x , E y , H x , H_y (см., например, [13]):

dF -

= M F .

dz

f E.

Здесь вектор-столбец F образован горизонтальными компонентами напряженностей поля волны

P j =

E y

H

F =

f E x 1 E y H

,

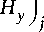
матрица M составлена из компонент тензора диэлектрической проницаемости и поперечных компонент волнового вектора

M ( n e ( z ), k ₁ ) =

—

к g ^{sin 9} k_x

—ky ick k xy

—

го ick y + i„

s zz g sin 9

s zz го gncos 9

C s

.   < 9 . 9

i го g ² sin ² 9

— s

^{— k}x

^{— k}y

-

го c \

^s zz

—

k x k y ic

ic k_x ²

—

^{— k}y

s zz го iго iC ky — c гos zz i (n —s)sin 29

—

2 s zz

. k gs^ y s zz

k

i (n —s)sin 29 2szz i (n —s)sin 29 2szz

iго sn c szz ick k xy

i го

—

—

го

ГОS zz   C ckxb. го szz i (n —s)sin 29

^x ^z^- n '

^s zz      /

;

ic _k 2 го

gncos9 го s zz    c

s zz = s sin ² 9 + n cos ² 9 .

В выражениях (5) использована система единиц СИ для напряженности электрического поля E и нормированная величина напряж еннос ти маг-

Дополним систему волновых уравнений (4)–(6) граничными условиями. Два из четырех условия определим на нижней границе z = 0, считая ее хорошим проводником:

E x ( z = 0) = 0, E_y ( z = 0) = 0.                             (9)

Чтобы получить два других граничных условия, поле волны F на уровне z = z _max представим как суперпозицию четырех мод

^{F (} z = z max ) = E A j P j .                              (1⁰)

j = 1

Здесь A_j – амплитуда и P _j – вектор поляризации j -й волновой моды при z = z _max.

Считая, что первый и второй корень относятся к падающей и отраженной волнам, а третий и четвертый – к нарастающему и затухающему в направлении оси z решениям, граничные условия при z = z _max запишем в виде

A 1 = 1, A 3 = 0.                                       (11)

Первое из этих условий задает величину поля в падающей волне, а второе исключает экспоненциально нарастающее решение в области z >  z _max.

Решая последовательно систему уравнений (4)– (6) с граничными условиями (9), (11), можно найти горизонтальное волновое поле E x y , H x y в области 0 <  z <  z _max. Вертикальные компоненты напряженностей E z , H z могут быть выражены через поперечные компоненты

E_z =— ( ( n —s )sin 9 cos 9 / s _zz ) E_y +                   (12)

+ ( ig sin 9 / s ) E + c ( k H — k H ) / zz x x y y x

/( гos _zz ) — icZ ₀ j_z /( гos _zz ),

нитного поля H = Z 0 H SI [14]; Z 0 =7^0

–

вол-

новое сопротивление вакуума; c – скорость света в вакууме. Значения плазменной концентрации (1) определяют величины электронной и ионной плазменных частот, частот столкновений заряженных частиц с нейтральными и, следовательно, элементы тензора диэлектрической проницаемости (3) и матрицы M (6). Собственные значения и собственные векторы матрицы

M( n e ( z ), k 1 , 0) P j = ik z(j) P j , j = 1 ^ 4

соответствуют локальным корням дисперсионного соотношения k z ( j ) и векторам поляризации j -й моды

H z = c ^{( k}y^Ex ^{— k}x^Ey )/ ^го .

E = — ( ( n —s )sin 9 cos 9 / s„ ) E + ( ig sin 9 / s_ _) E + z                                zz y                 zz x

+ c ^{( k}x^Hy ^{— k}y^Hx ^{)/( ГОS} zz ), H z = c ^{( k}y^Ex ^{— k}x^Ey ) I ^го .

В частности, горизонтальное магнитное поле H 1 ( z = 0) на поверхности Земли и коэффициент отражения по энергии сверху равны, соответственно: H ₁ ( z = 0) = H 2 ( z = 0) + H 2 ( z = 0).                 (13)

R = S zr ¹,                                            (14)

^Sz ( i )

где S ir = (2 Z 0 ) ^{— 1} Re[ E ₁ ir , H ₁ i r ] - вертикальные составляющие вектора Пойнтинга падающей ( i ) на

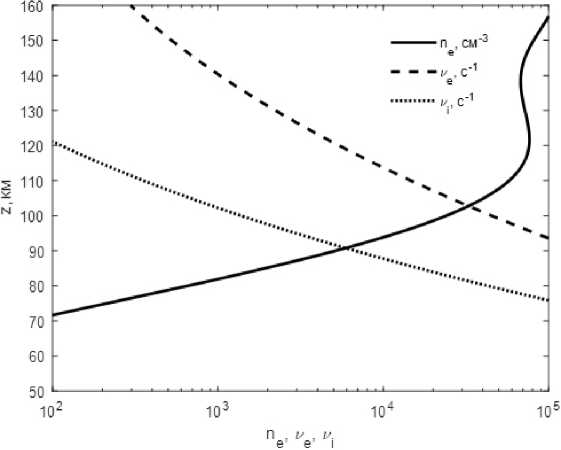
Рис. 2. Высотные профили плазменной концентрации (сплошная линия) частоты столкновений электронов (пунктирная линия) и ионов (кор. пунктирная линия) с нейтральными частицами

Fig. 2. Altitude profiles of plasma density (solid line) and collision frequencies of electrons (dotted line) and ions (dashdot line) with neutral particles

границу z = z _max волны и отраженной ( r ) от этой границы.

2. Результаты расчетов. Обсуждение

Для расчетов использованы профили плазменной концентрации и частот столкновений заряженных частиц с нейтральными, изображенные на рис. 2. Данные для плазменной концентрации получены с помощью модели IRI [15] и соответствуют 50 ° с. ш. и 40 ° в. д. 1.IV.2020 г., 6.00 по местному времени. Угол между направленной вверх вертикальной осью z и магнитным полем при этом равен 9 = 157 ° . Зависимости частот столкновений заряженных частиц с нейтральными соответствуют данным, приведенным в книге [16]. Зависимость возмущений плазменной концентрации (1) соответствует инфразвуковой ветви акустико-гравитационных волн, фазовая скорость которых порядка скорости звука и пренебрежимо мала по сравнению с фазовой скоростью электромагнитных волн свистового диапазона.

Численное решение уравнений (4)–(6), (9), (11) получено с помощью решателя обыкновенных дифференциальных уравнений bvp4c Mathlab. Решатель является конечно-разностным кодом, реализующим формулы коллокации для граничной задачи [17]. Метод основан на решении начальной задачи с параллельным решением алгебраического уравнения для уточнения «пристрелки». В рассматриваемом случае граница падения излучения составила zmax = 150 км. Во-первых, при таком выборе верхней границы удается получить численно стабильное решение системы волновых уравнений. Во-вторых, выше этой границы для свистовой волны рассматриваемого диапазона выполняются условия плавной неоднородности плазмы |кjЛz| » 1, где Лz - масштаб неоднородности плазмы и кj - волновое число свистовой волны. В-третьих, значения коэффициентов отражения и прохождения к Земле определяются в основном процессами в нижней части ионосферы [18]. Значения магнитной напряженности при расчетах были нормированы на величину электрической напряженности в падающей волне

E i = ⁽ E 2 i ) + $ i ) + E 2( i ) ^{) 1/2}|_ .

z z max

Примеры результатов расчетов для свистовых волн с частотами 0,85 кГц и 1,5 кГц приведены на рис. 3–5. На рис. 3 представлено решение дисперсионного соотношения (7) для невозмущенной ионосферной плазмы ( Л n e = 0) при n ₁= k ₁ c / ш = 0. Из приведенных графиков видно, что мнимая часть вертикального показателя преломления n z = k z c / ш распространяющихся волновых мод увеличивается в несколько раз в относительно локальной по высоте области 80–110 км. Следовательно, характеристики распространения и отражения свистовых волн могут быть особенно чувствительны к возмущениям плазменной плотности именно на этих высотах. Поскольку значения показателя преломления на этих высотах много больше единицы, приведенные зависимо-

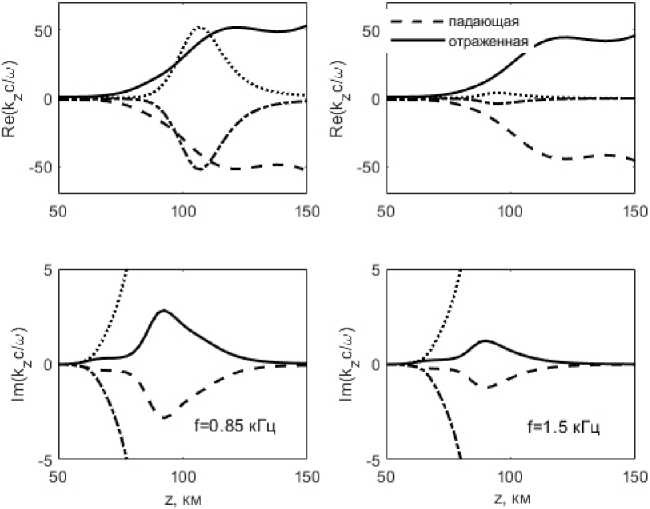
Рис. 3. Решения дисперсионного соотношения для реальной и мнимой частей показателя преломления n z = k z c / ш Fig. 3. Dispersion relation solution for the real and imaginary part of the refractive index n z = k z c / ш

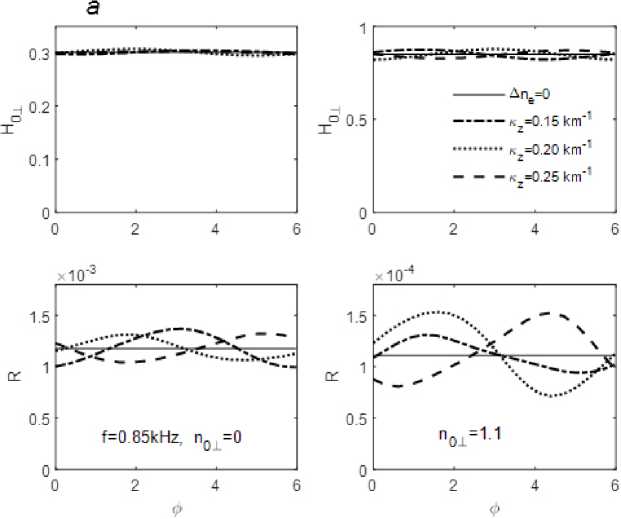
Рис. 4. Нормализованная амплитуда магнитного поля H _{0 ⊥} на земной поверхности и коэффициент отражения R от ионосферы сверху при различных параметрах инфразвуковой волны. Частота свистовой волны f = 0,85 кГц

Fig. 4. Normalized amplitude of wave magnetic field H _{0 ⊥} on the Earth’s surface and the reflection coefficient R from the ionosphere from above for different parameters of the infrasonic wave. The frequency of whistler wave is f = 0,85 kHz

сти справедливы также для наклонно падающих волн с горизонтальными компонентами n _⊥ порядка единицы или нескольких единиц.

На рис. 4 (для свистовой волны с частотой 0,85 кГц) и 5 (для свистовой волны с частотой 1,5 кГц) изображены зависимости нормализованной амплитуды магнитного поля на земной по- верхности H0⊥ (13) (именно эта величина обычно измеряется в наземных обсерваториях) и коэффициента отражения от ионосферы сверху R (14) от фазы инфразвуковой волны φ. Графики соответствуют глубине модуляции в инфразвуковой волне A ne / ne 0 = 0,07 и значениям вертикальной длины инфразвуковой волны волны 2р / кz 42 км (1,5),

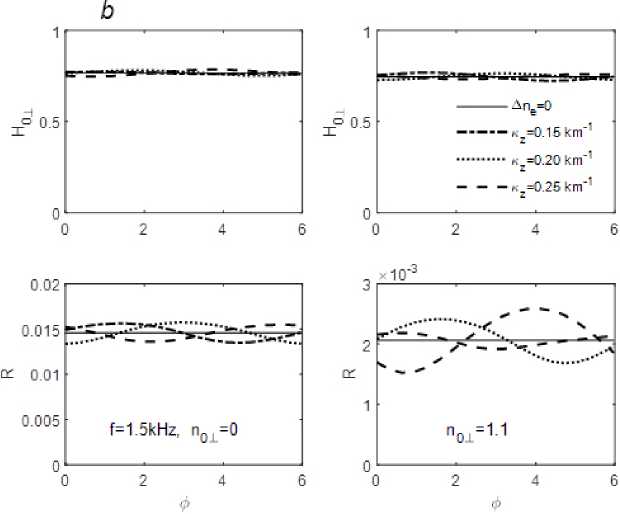
Рис. 5. Нормализованная амплитуда магнитного поля на земной поверхности H _0± и коэффициент отражения R от ионосферы сверху при различных параметрах инфразвуковой волны. Частота свистовой волны f = 1,5 кГц

Fig. 5. Normalized amplitude of wave magnetic field H _0± on the Earth’s surface and the reflection coefficient R from the ionosphere from above for different parameters of the infrasonic wave. The frequency of whistler wave is f = 1,5 kHz

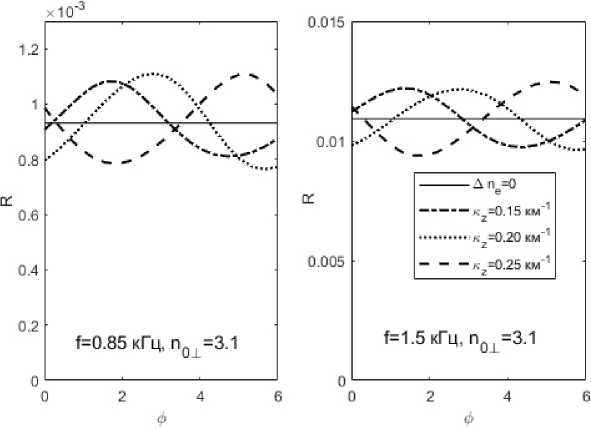
Рис. 6. Коэффициент отражения R свистовой волны от ионосферы сверху вне «конуса выхода» при различных параметрах инфразвуковой волны

Fig. 6. The reflection coefficient R of whistler wave from the ionosphere from above out of «exit cone» for different parameters of the infrasonic wave

31 км и 25 км. Графики в левой части рис. 4, 5 соответствуют нормальному падению волны n ± = 0. Графики в правой части рис. 4, 5 приведены для случая Пу = 1,1, что практически соответствует границе «конуса выхода» свистовой волны к земной поверхности. На рис. 6 приведены зависимости коэффициента отражения R (14) от фазы ф для случая наклонного падения с Пу = 3,1. Так как в этом случае волна не достигает земной по- верхности, магнитное поле H о± становится на несколько порядков ниже.

В случае нормального падения свистовой волны (nу = 0) при глубине модуляции плазменной плотности 7 % вариации магнитного поля H о± не превышали 2 % (при f = 1,5 кГц) и 3,3 % (при f = = 0,85 кГц), тогда как вариации коэффициента отражения R могли достигать 7,5 % (при f = 1,5 кГц) и 15 % (при f = 0,85 кГц). В случае наклонного па- дения свистовой волны вблизи границы «конуса выхода» (n у = 1,1) вариации магнитного поля H о1 достигали 3,5 %, вариации коэффициента отражения были еще значительнее и составили 18 % (при f = 1,5 кГц) и 38 % (при f = 0,85 кГц). В случае наклонного падения свистовой волны вне «конуса выхода» (nу = 3,1) магнитное поле Hоу на несколько порядков ниже, вариации коэффициента отражения - 15 % (при f = 1,5 кГц) и 19 % (при f = = 0,85 кГц).

Магнитное поле H о у и коэффициент отражения R наиболее чувствительны к возмущениям плотности в зоне сильного затухания свистовой волны (для рассматриваемых частот 80–110 км, см. рис. 3).

Заключение

Рассмотрена задача о влиянии возмущений плазменной плотности, вызванной инфразвуковыми волнами, на отражение и распространение электромагнитных волн свистового диапазона, падающих на утреннюю ионосферу сверху. Исследована взаимосвязь коэффициента отражения свистовой волны от ионосферы сверху, поля электромагнитной волны на земной поверхности и параметров инфразвуковой волны.

Влияние возмущения плазменной плотности на отражение и прохождение низкочастотных элек- тромагнитных волн через ионосферу существенным образом зависит от высоты локализации этого возмущения. Наиболее сильные изменения коэффициента отражения обусловлены изменениями плазменной концентрации на высотах 80– 110 км, где декремент затухания распространяющихся мод излучения увеличивается более чем на порядок в пределах достаточно локальной по высоте области. Относительное изменение коэффициента отражения свистовой волны в этом случае может достигать почти 40 % при глубине модуляции плазменной концентрации 7 %. При этом более существенные изменения коэффициента отражения имеют место для волн с меньшей частотой и волн вблизи границы «конуса выхода», то есть при близких к единице значениях поперечного показателя преломления. Максимальное относительное изменение горизонтального волнового магнитного поля на земной поверхности при этом не превышает 3,5 %.

Полученные результаты актуальны для понимания взаимосвязи волновых процессов в магнитосфере. В частности, вызванные инфразвуковыми волнами неоднородности ионосферной концентрации объясняют возможность сильной модуляции добротности резонатора в плазменном магнитосферном мазере.