Волоконно-интерференционный метод получения неоднородно поляризованного пучка

Наблюдению поляризационных эффектов света посвящено большое число исследований. В последнее время возрос интерес к световым полям, имеющим неоднородную поляризацию. Наибольший практический интерес представляют пучки с радиальной и азимутальной поляризацией. Такие пучки применяются для решения разнообразных задач в лазерной микроскопии сверхвысокого разрешения [1–3], лазерной манипуляции [4–7], медицинской диагностике [8], в технологических процессах обработки металлов [9–11], для ускорения электронов [12–14], для исследования плазмонов [15].

Формирование множества различных типов векторных поляризационно неоднородных мод с уникальными свойствами осуществляется с помощью дополнительных внутри- или внерезона-торных устройств [16]. Внутрирезонаторные методы основаны на модификации лазерных резонаторов. Главный недостаток такого метода состоит в том, что он ориентирован на конкретный тип лазеров и, как правило, на получение какого-то одного типа неоднородной поляризации.

Синтез неоднородно поляризованных пучков с помощью внешних устройств либо интерференционных схем относится к внерезонаторным методам. Главным преимуществом внерезона-торных методов является универсализм, недостатком – сложность выполнения. Принцип действия поляризационных устройств основан на локальном изменении состояния поляризации в каждой точке поперечного сечения лазерного пучка.

Целью данной работы является разработка волоконно-интерференционного метода получения неоднородно поляризованного по сечению светового пучка.

Анализ распространения циркулярно поляризованного излучения в оптическом волокне

Рассмотрим распространение излучения в оптическом волокне со ступенчатым профилем показателя преломления [17].

Пусть на вход волокна падает циркулярно поляризованная волна со спиновым моментом о =+ 1:

1,1

E ⁺ ( r ф z = 0 ) =  .K e - ^Ф У C _^ ( r ) + У У C _ , _m N e " ""^ ( r ) + УУ C ₊ , _т , N/m J m , „ ( r ) [ ,

V°Z) I    N              m *1 N                    mN.

где

f 1 )

и C _{+ 1 N} определяют вклад мод

- столбец Максвелла [18], о = +1, коэффициенты C ] N \Oi)’ ’ e+ m N (r, Ф) и e-+ m N(r, Ф) в световое поле на входе в волокно. На выходе из волокна имеем сле- дующее распределение поля:

Большаков М.В., Гусева A.В., Кундикова Н.Д., Попков И.И.

^{Е +} ( r, 9 , z ) = Ч ZZ С - , _m , N e ^{im 9} F m N ( r ) • exp - iz ( p _m N + Sp ^N ) ! + V i J I m / 1 N                             ^{L                    j}

+ Z Z C . m , N e ⁺ i^N ( r ) exp Г iz ( P m , N + «& ) 1 + mN

+ Z С -_Д , _Ne ^- 91 _N ( r ) e^ f e 2 z^ N + 14 +

N                          V            J,

+

- i

e ⁹ Z C - , 1N F 1N ( r ) N

e i^, N

e i ² e N

где 5p m'N — поляризационная поправка к константе распространения моды с индексами m ,

Fm N (r) — радиальная функция. Аналогичные выражения можно записать и для случая, когда на вход волокна падает излучение со спиновым моментом о = -1.

Из выражения (1) следует, что на выходе из волокна появляется излучение с противоположным спиновым моментом о = -1 («чужая» поляризация), вклад в которое дают только моды e2N и e4N. Эти моды являются особыми, т.к. они соответствуют меридиональным лучам, для кото рых циркулярная поляризация не сохраняется в силу условий симметрии [17, 19].

Если на выходе из волокна поставить «циркулярный анализатор», пропускающий циркулярное излучение со знаком, противоположным знаку о на входе в волокно, то через него пройдут только соответствующие моды с орбитальным моментом m = 1 . Если после поляризатора поставить четвертьволновую пластинку, то прошедшая волна может приобрести любую поляризацию, в том числе и циркулярную. Пусть после четвертьволновой пластинки распространяется циркулярно поляризованное излучение с m = 1. Рассмотрим подробнее поле, прошедшее через «циркулярный анализатор». Этот анализатор состоит из четвертьволновой пластинки и поляризатора. Поле описывается последним членом в сумме в (1). Если на вход волокна падает свет со спиновым моментом о = + 1, то поле, прошедшее через анализатор, будет иметь следующий вид:

^{е +} ( r , 9 ) =

j. | e • | z C - ,1 N F 1, N ( r ) e i^N Г e i ² z⁵⁸^ - 1

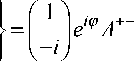
V i JI N                       -

Если на вход волокна подавать излучение со спиновым моментом о = - 1, то поле, прошедшее через анализатор, будет иметь вид:

^{Е +} ( r , 9 ) =

e ² z< N - 1 I = a ■

J e ^- i ⁹ • U С +.1.N F 1.N ( r ) е" ^{в |} , ”

V+i J      I N

Если выровнять интенсивности этих двух пучков, то есть сделать равными коэффициенты

A ⁺ = A ⁺ = A , то результирующее поле имеет следующий вид:

Е ⁺ ( r , 9 , z ) + Е ⁺ ( r , 9 , z ) =

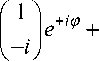
V+i J

A = Е ² ( r , 9 , z ) A .

Распределение поляризации в поперечном сечении поля (1) на выходе волокна определяется выражением:

Е ² ( r , 9 , z ) =

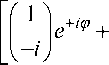
V

_e- i ⁹

Легко показать, что

Е ^L ( r , 9 , z ) =

V 1

V^{- i}

e+i9

V+i J

e -^{i 9}

= 2

v cos 9

_V sin 9

f £-i

V Ey J

Поляризацию в каждой точке поперечного сечения суммарного пучка можно определить, ис пользуя комплексное число х = Ey,Ex . Угол наклона эллипса поляризации 9 определяется вы- ражением:

Краткие сообщени^

а угол эллиптичности £ :

tg (20 ) =

2Re ( X )

sin (2г) =

^2Im ( X )

^{1 +} W ²

Из выражения (2) следует, что х = sin ф /cos ф = tg ф и, следовательно:

tg (20 ) =

2W

1 - |tg ф 2’

откуда следует, что 0 = ф , т.е. наклон эллипса поляризации задается азимутальной координатой. Так как число х — действительное, то в соответствии с выражением (3) sin ( 2 г ) = 0, следовательно, эллиптичность тоже равна нулю и излучение является линейно поляризованным.

Таким способом можно получить пучок с неоднородно распределенной по сечению линейной поляризацией, а именно, в каждой точке сечения колебания вектора электрического поля направлены по радиусу сечения.

Рассмотрим случай, когда в один из пучков внесена разность фаз п . Тогда выражение приобретает следующий вид:

Рассмотрим отдельно член, который определяет поляризацию:

e+i ( ф+ ^п )

^ sin ф v COSф

E x E

Из выражения (4) следует, что х = sin ф /cos ф = tg ф , и, следовательно:

откуда следует, что 0 = - ( ф + П 2), т.е. большая ось эллипса поляризации перпендикулярна радиусу. Угол эллиптичности в данном случае равен нулю, следовательно, эллиптичность тоже равна нулю.

Таким образом, можно получить линейно поляризованное излучение, направленное азимутально, т.е. направление поляризации перпендикулярно радиусу.

Складывая такие пучки с различным соотношением фаз, можно получить различные неоднородно поляризованные по сечению пучки.

Таким образом, на основе анализа распространения излучения в оптическом волокне показано, что излучение, вышедшее из оптического волокна, можно использовать для получения неоднородно линейно поляризованных пучков, в частности, поляризованных радиально или азимутально.